Teselados II

Teselados II

Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.

Énfasis: analizar las características de los teselados para recubrir un plano con un diseño propio.

¿Qué vamos a aprender?

El día de hoy analizarás las características de teselados para que posteriormente puedas crear tu propio diseño.

¿Qué hacemos?

Para iniciar, ¿qué observas en la siguiente imagen?, ¿qué formas tiene?, ¿qué piensas que es?

Se trata de una iguana

Ahora otra imagen, ¿qué observas?, ¿de qué piensas que se trata?, ¿puedes saber qué es?

Es una serpiente jarretera o también conocida como culebra rayada. ¿Sabías que las hembras se distinguen por ser más largas que los machos? Pueden llegar a medir hasta 1 metro y tener hasta 80 crías.

Si te interesó este dato, te invitamos a investigar más, encontrarás información muy sorprendente.

Observa esta otra imagen. ¿Te es familiar? Observa detenidamente la superficie, ¿qué formas encuentras?, ¿ya sabes de qué se trata?

Efectivamente, es una piña.

Ahora la última imagen. ¿Qué observas?, ¿Conoces las figuras que hay en ella?, ¿puedes identificar de qué se trata?

Se trata de un museo ubicado en la Ciudad de México, único por su arquitectura y además contemporáneo, es el museo Soumaya. Fue diseñado por el arquitecto, mexicano, Fernando Romero. El museo se inauguró en el año 2011, tiene fuerte impacto por su forma, pero, además porque está cubierto por hexágonos de aluminio.

Ahora observa, ¿Qué tienen en común las imágenes?

Dos imágenes corresponden a animales, una a una fruta y otra a un edificio, pero ¿qué características tienen en común?, ¿cómo son las formas que tienen en su superficie? En la iguana solamente es un tipo de polígono irregular el que se repite, mientras que, en la serpiente, además de tener cierta regularidad en las formas, también tiene una regularidad en los colores. La piña, se forma por dos figuras, una es un polígono irregular y la otra se asemeja a un semicírculo y, por último, el museo, se forma por polígonos regulares, que son hexágonos.

A pesar de que muestran diferentes polígonos o formas estos animales, frutas y arquitectura coinciden en que siguen un patrón o regularidad y recubren perfectamente toda su superficie. ¿Sabes, cómo se le llama a ese patrón?

A ese patrón se le llama: Teselado. Un teselado es un patrón de figuras o polígonos que se repiten con regularidad para cubrir el plano o una superficie plana. Observa y analiza bien estas imágenes, que corresponden a ejemplos de teselados.

¿Puedes identificar sus características?, ¿sabes por qué pueden cubrir el plano?

Las principales características de un teselado son:

• Debe cubrir todo el plano, sin que haya espacios, como el ejemplo de los hexágonos azules.
• Las figuras o polígonos no deben superponerse, es decir no puede quedar una encima de otra.
• Al coincidir un vértice de cada figura en un punto, la suma de los ángulos que ahí coinciden debe ser de 360 grados.

Hay 3 tipos de teselados: los regulares, los semirregulares y los irregulares.

Los teselados regulares, son aquellos que cubren el plano con polígonos regulares. Sin embargo, solamente hay tres polígonos regulares con los que se puede cubrir completamente el plano, el triángulo equilátero, el cuadrado y el hexágono.

Esto se debe a que, si se unen, un vértice de cada polígono, en un mismo punto, los ángulos internos que ahí coinciden suman un ángulo de 360 grados.

En el caso del triángulo equilátero, coinciden, 1, 2, 3, 4, 5 y 6 triángulos en un punto Recuerda que cada ángulo interno del triángulo equilátero mide 60 grados, por lo que multiplicando 60 grados por 6, se obtienen 360 grados.

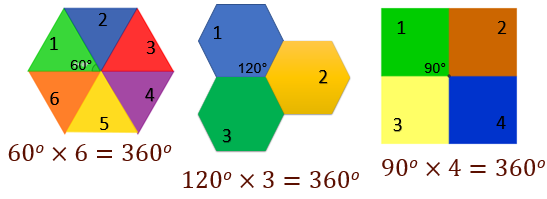
En el hexágono coinciden 1, 2, 3 figuras de éstas. Sabemos que sus ángulos interiores miden 120 grados, por lo que se multiplica 120 grados por 3 y se obtiene 360 grados.

Ahora para el cuadrado: se unen en un mismo punto 1, 2, 3 y 4 cuadrados. Como sabemos, los ángulos internos de esta figura miden 90 grados, por lo que entonces se multiplica 90 grados por 4 y también se obtienen 360 grados.

Ahora, los teselados semirregulares: son aquellos que cubren el plano combinando dos o más polígonos regulares.

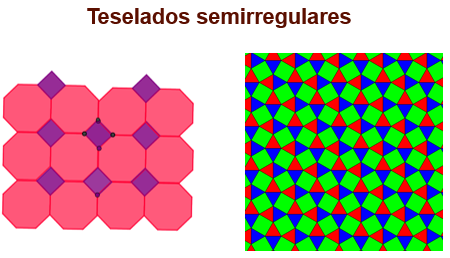
El primer teselado se forma con octágonos regulares y cuadrados.

El segundo está compuesto por triángulos equiláteros y cuadrados.

Cabe destacar que solamente se pueden formar ocho teselaciones semirregulares, Algunas variaciones pueden ser en los colores, pero al final es la misma isometría la que se repite.

Con isometría nos referimos a la transformación geométrica que tienen las figuras, como la rotación o traslación.

Los teselados irregulares se forman con la combinación de polígonos regulares e irregulares, y pueden tener un patrón que pueda ir recubriendo el plano.

Observa el ejemplo, ¿pueden identificar los polígonos se usan en el teselado?

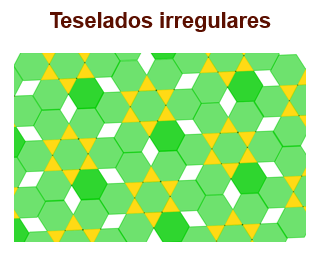
Se utilizan hexágonos, triángulos y rombos. El triángulo y el hexágono que se usan en este teselado son regulares, pero no lo es el rombo, este tipo de combinaciones son las que destacan a los teselados irregulares.

Como viste al inicio, los teselados se pueden encontrar en la naturaleza, en algunas plantas, animales y minerales. También se encuentran en la arquitectura, en obras de arte, en vitrales y en la vida cotidiana, por ejemplo, en pisos y puertas, entre otros.

En el día a día, lo más común es encontrarlos en los pisos, cuando vas por el parque, en la calle, en la plaza, en los mismos hogares.

En nuestros hogares, podemos encontrarlos ocasionalmente en las paredes, en los pisos, en las cortinas, en las puertas, en decoraciones, en ropa, etcétera.

Para que quede más claro, observa ver el siguiente vídeo:

1. Mosaicos y teselados en Secundaria

Tekman education

https://www.youtube.com/watch?v=agjBv-34tGg

Conociste el mayor creador de teselados, Maurits Cornelis Escher, él destaca gracias a su surrealismo; ya que creaba obras que eran imposibles, les daba un toque tridimensional y lograba engañar al ojo del espectador. En sus obras usaba colores llamativos, pero también le gustaba trabajar con blanco y negro.

En el video pudiste darte cuenta de que usó algunas isometrías para poder recubrir el plano y sus figuras partían de polígonos regulares, solamente les hacía transformaciones que después desplazaba hacia otro lado de la figura para que pudieran embonar a la hora de recubrir el plano.

Es importante destacar que, para formar teselados, no hay algún procedimiento específico, más bien depende de la creatividad de cada uno.

A continuación, vas a realizar un teselado, siguiendo el procedimiento que utilizó Escher.

Lo más importante es dejar fluir la creatividad. Posteriormente, diseñar una plantilla que pueda recubrir el plano, tomando en cuenta las características anteriormente vistas.

Vas a partir de una de las figuras más sencillas, el cuadrado. Para ello:

• Traza el cuadrado ABCD, te recomendamos que el cuadrado sea de 4 o 6 centímetros por lado.
• Posteriormente, ubica los puntos medios de cada lado del cuadrado. Al punto medio de AB, le llamamos E; al punto medio de BC, le llamamos F; al punto medio de CD, le llamamos G y al punto medio de DA, le llamamos H.
• Vas a trazar un punto medio del segmento DG, que será el punto I (i).
• Traza una semicircunferencia con radio DI y centro en I. De esta manera se determina un semicírculo que quedará dentro del cuadrado.
• Traza el punto medio de CG como centro de otra semicircunferencia de radio CG. El semicírculo así determinado quedará fuera del cuadrado.
• Posteriormente, este trazo de los semicírculos se replica en el lado AB del cuadrado.
• Continua con el mismo procedimiento para el lado AD, se traza una semicircunferencia que quede dentro del cuadrado.
• Posteriormente, se replican estos trazos al lado BC.

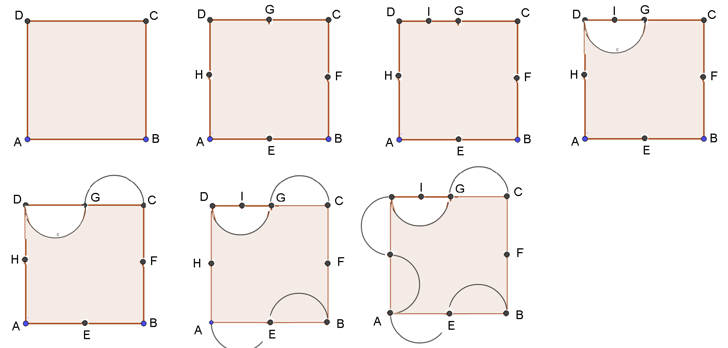
Si se recortan las semicircunferencias se obtiene una figura como la que se muestra.

La figura recortada anterior será con la que se va a recubrir el plano.

Te invitamos a que recubras una hoja blanca con esa plantilla. Luego, identifiques dos figuras cualesquiera, puedes hacerlo con un mismo color o con un número.

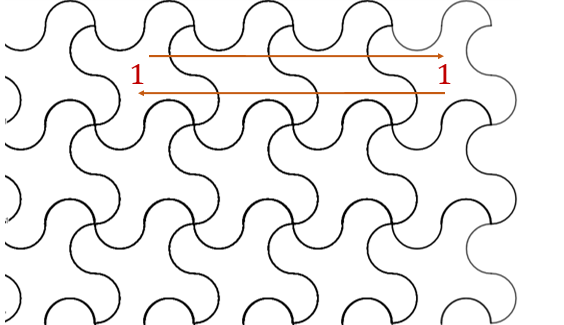
Ahora, identifica la transformación que puede aplicarse en una para determinar el lugar de la otra. Se aplica una traslación, de derecha a izquierda o viceversa, como indican las flechas. Recuerda que, en este caso del cuadrado, para obtener la plantilla, los trazos que se realizaron en un lado se hicieron, en la misma posición, en el lado paralelo. ¿Puedes relacionar estas isometrías con algunos movimientos de las figuras?

En estos casos puedes usar la simetría axial, la simetría central, la rotación y también la traslación.

Para el siguiente ejemplo, te basaras en los mosaicos Nazaríes. Estos mosaicos son muestra de la cultura de los musulmanes, quienes fueron expertos en la geometría basada en la composición de movimientos en el plano. En esos mosaicos se distinguen muchos teselados. De los más destacados en la artesanía islámica son: el Hueso, el Pétalo, la pajarita y el avión, entre otros.

Sus mosaicos son de los más bellos, por su estructura geométrica exacta.

A continuación, realizarás un acercamiento al teselado nazarí, el avión. Para ello, vas a partir nuevamente del cuadrado. Sigue el procedimiento con un cuadrado de 6 centímetros por lado.

Te recomendamos poner letras en cada vértice del cuadrado para seguir las instrucciones.

• Inicia con el cuadrado ABCD
• Se localizan los puntos medios de cada lado. El punto medio del lado AB, es I; el punto medio del lado BC es F; G es el punto medio del lado CD y el punto medio del lado AD es el punto H.
• Posteriormente se trazan dos ejes de simetría del cuadrado que unan los puntos medios de lados opuestos, es decir, se une G con I mediante un segmento, y también F con H.
• El punto de intersección de los segmentos GI y FH, queda en el centro del cuadrado y lo llamamos K.
• Se ubica el punto medio del segmento KH, que llamaremos con la letra L.
• Se unen los puntos G con L.
• Se ubica el punto medio del segmento AH y se le nombra punto M.
• Se unen los puntos M con I.
• Continua con los trazos uniendo puntos medios de los segmentos involucrados.

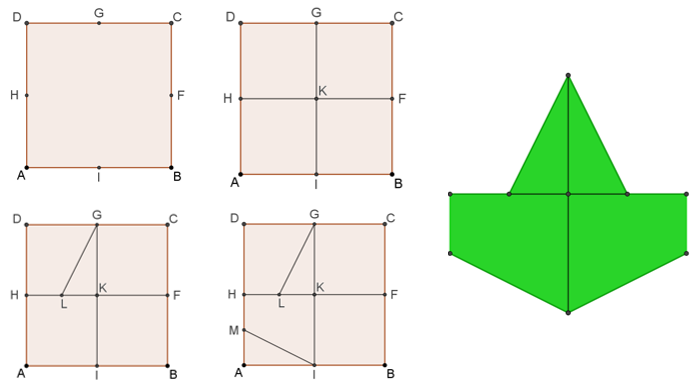
Para poder obtener la plantilla, recorta el contorno de los trazos realizados, como se muestra en la imagen. Debes obtener un polígono irregular. Borra todas las líneas para que tu plantilla quede limpia.

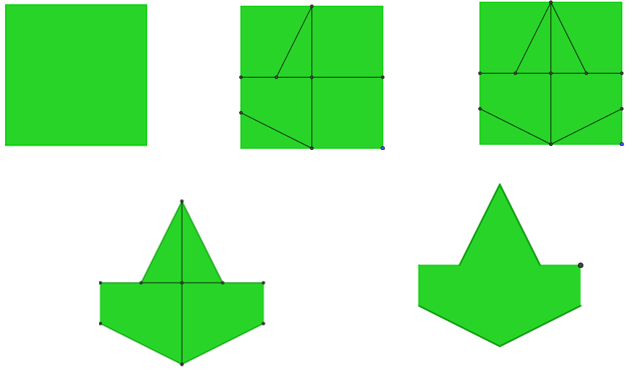
Una vez obtenida la plantilla se inicia con el recubrimiento del plano. En media cartulina ve copiando o calcando la plantilla. La plantilla se puede ir rotando, cuidando que no se encime de una figura ya trazada, también la puedes ir trasladando.

Puedes ir coloreando de diferentes colores para que se distingan las isometrías, además de que el mosaico es más atractivo visualmente. Observa que se van repitiendo los patrones. Has formado un teselado nazarí.

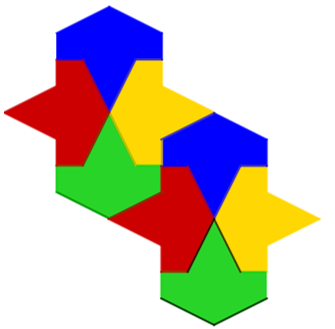
Verás ahora algunos los movimientos que pueden hacer con esa figura para cubrir el plano.

¿Qué se hace con una figura azul, para ubicarla en donde se encuentra la otra de ese mismo color? Esas figuras se pueden colocar una encima de la otra mediante una traslación.

¿Qué se hace con una figura azul, para ubicarla en donde se encuentra la otra de color verde?

Aquí puedes distinguir una rotación.

¿Qué te parece el trabajo con teselados?

Para evaluar lo que has aprendido hasta el momento da respuesta a los siguientes cuestionamientos. Anota tus conjeturas en el cuaderno para que, posteriormente, las compares con la información que se te presenta.

¿Qué es un teselado?

1. Es un diseño personal.
2. Se forma con polígonos irregulares y puede haber espacios.
3. Es un patrón o regularidad que cubre completamente un plano.
4. Recubre el plano combinando dos o más polígonos regulares.

Aunque se puede decir que puede ser un diseño personal, la característica más importante de las 4 opciones, es que se trata de un patrón o regularidad que cubre completamente el plano, además se pueden formar teselados combinando polígonos regulares.

¿Cuáles son las características de un teselado semirregular?

1. Recubre el plano con polígonos regulares.
2. Se forma con polígonos regulares y puede haber espacios.
3. Se forma con polígonos irregulares.
4. Recubre el plano combinando dos o más polígonos regulares.

La opción correcta es la d. Ya que un teselado semirregular recubre el plano combinando dos o más polígonos regulares.

¿Cuáles son las características de un teselado regular?

1. Recubre el plano con polígonos regulares: el triángulo, cuadrado y hexágono.
2. Se forma con polígonos regulares y puede haber espacios.
3. Se forma con polígonos irregulares.
4. Recubre el plano combinando polígonos regulares e irregulares.

La opción correcta es la a. Ya que un teselado regular recubre el plano con polígonos regulares: el triángulo, cuadrado y hexágono

¿Cuáles son características de un teselado?

1. Que haya huecos y que no se superpongan las figuras
2. Que no queden huecos y se superpongan las figuras
3. Que no se puedan rotar y trasladar las figuras para colocar una encima de otra.
4. Que no queden huecos ni se superpongan las figuras.

La opción correcta es la d, porque en los teselados no debe haber huecos entre las figuras ni se deben superponer una en otra.

¿Cómo se clasifican los teselados?

1. Por el color de las figuras que lo forman.
2. Por el tamaño de las figuras que lo forman.
3. Por el tipo de figuras que lo forman.
4. Por los ángulos de las figuras que lo forman.

Por el tipo de figuras que lo forman. Recuerda que esos teselados pueden ser regulares, semirregulares o irregulares.

¿Cuáles son las características de un teselado irregular?

1. Recubre el plano con polígonos regulares: el triángulo, cuadrado y hexágono.
2. Recubre el plano combinando polígonos regulares e irregulares.
3. Se forma con polígonos o figuras irregulares.
4. Se forma con polígonos regulares y puede haber espacios.

La opción correcta es la b. Un teselado irregular recubre el plano combinando polígonos regulares e irregulares.

Si se tiene un cuadrado, un octágono regular y un triángulo equilátero, con la misma medida en sus lados, y se juntan lado a lado, ¿se puede formar un teselado con estas figuras?, ¿por qué?

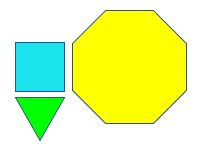
La respuesta correcta es: no. Esto se debe a la medida de los ángulos interiores del triángulo es de 60 grados, los del cuadrado, 90 grados y los del octágono regular, 135 grados. Y si se suman 90 grados más 60 grados, más 135 grados, se obtienen 285 grados, lo que significa que quedaría un espacio y no se cumpliría con una característica de un teselado que es que no quede ningún espacio libre.

¿Cuáles son los polígonos regulares con los que se pueden formar teselados regulares?

Solamente son tres. Únicamente son el triángulo equilátero, el cuadrado y el hexágono regular.

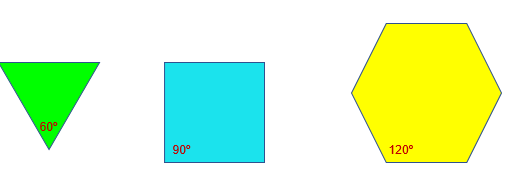
¿Cómo debe ser la medida del ángulo de un polígono regular para que pueda recubrir el plano?

Recuerda que los ángulos interiores del triángulo equilátero miden 60 grados, los del cuadrado miden 90 grados y, los del hexágono regular, 120 grados. La medida de los ángulos interiores de las figuras mostradas son divisores de 360 grados. Y esa es la condición para que con un polígono regular se pueda teselar el plano, ya que el ángulo que se forma al unirse en un mismo punto los vértices de los polígonos es de 360 grados.

Observa bien las siguientes figuras y contesta.

¿Piensas que con la siguiente figura se puede recubrir el plano?

Si respondiste que sí, es correcto ya que al ir trasladando la figura no se encima en otra y tampoco deja espacios sin cubrir.

¿Con cuál o cuáles de las siguientes figuras se puede cubrir un piso?

Las figuras anteriores tuvieron como base un hexágono; sin embargo, no con todas se puede recubrir el plano, Con las figuras que se puede cubrir un piso son la figura amarilla y la azul.

Este tema te permite ver la diversidad y variedad que existe en las matemáticas y en geometría. Te puedes dar cuenta que la geometría se encuentra en muchas partes y en diferentes campos, además de que se puede relacionar con otras disciplinas como lo es el arte.

El reto de hoy:

Realiza tu propio diseño de una plantilla; elige qué tipo de teselado vas a crear, regular, semirregular o irregular. Toma en cuenta los aspectos revisados durante la sesión, para que cumpla con los requisitos y características específicas de un teselado. Pon colores llamativos y cubre al menos media cartulina con tu diseño.

Guarda tus evidencias para que posteriormente las puedas compartir con tus compañeras y compañeros, así como con tu profesora o profesor.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html