Teselados IV
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
Teselados IV
Aprendizaje Esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: analizar las características de los teselados para su construcción II.
¿Qué vamos a aprender?
En esta sesión construirás teselados con ayuda de una aplicación de geometría dinámica: GeoGebra.
Ten a la mano tu cuaderno, lápiz o bolígrafo, para que anotes tus dudas, inquietudes o dificultades que surjan al resolver los planteamientos que verás en esta sesión.
¿Qué hacemos?
La palabra teselados proviene de "tessellae", que así era como llamaban los romanos de la antigüedad, a las construcciones y pavimentos de su ciudad.
Pero, ¿qué es un teselado?

Aunque se ha dicho que los teselados cubren planos, en esta sesión construirás un teselado que permita cubrir un espacio en tercera dimensión.
Teselaciones en 3D.


Llevarás a cabo, algunas construcciones de teselaciones con la aplicación de la geometría dinámica GeoGebra.
Antes de comenzar debes configurar ciertas condiciones en la interfaz de GeoGebra. En la siguiente imagen, verás la interfaz de GeoGebra Clásico al abrirlo.
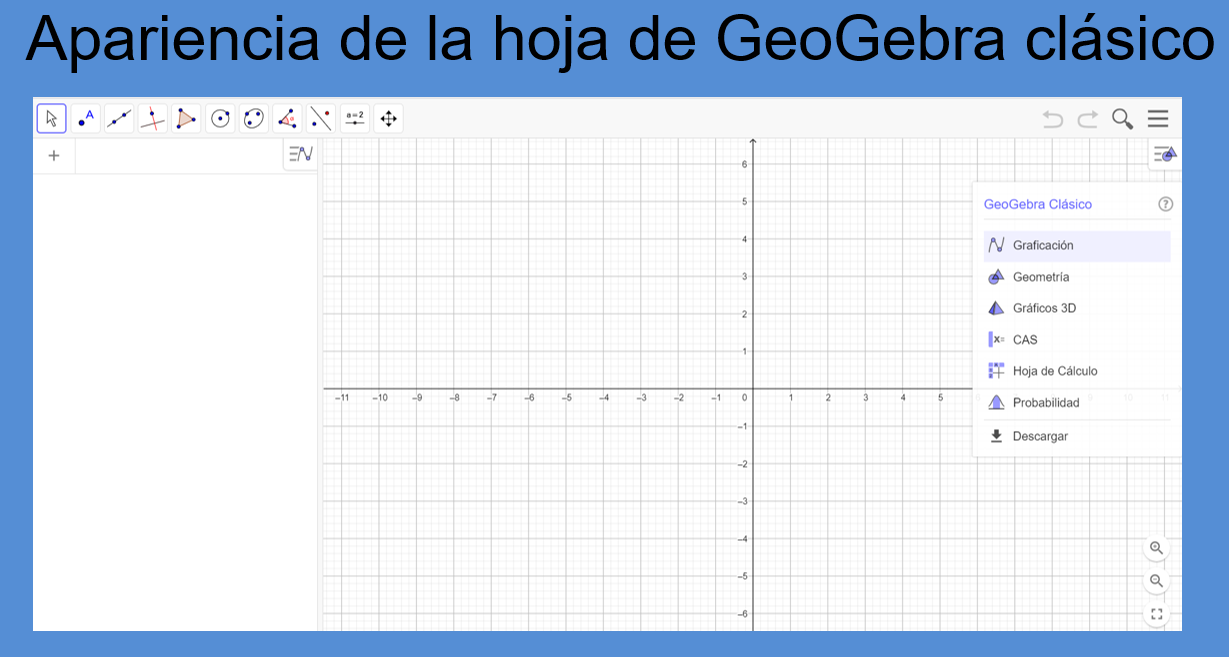
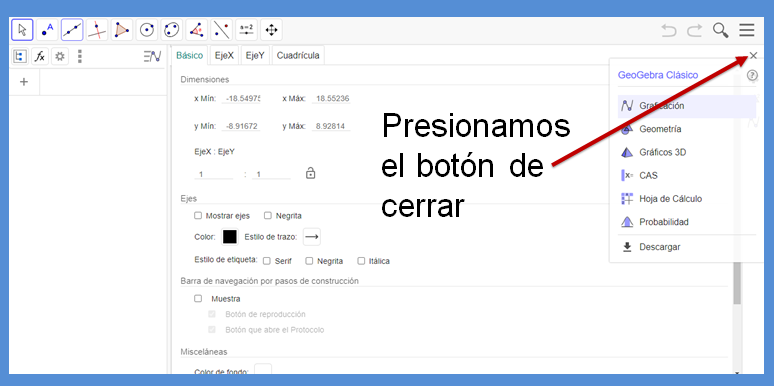
Lo primero que harás es cerrar una ventana que se encuentra en la parte superior derecha.
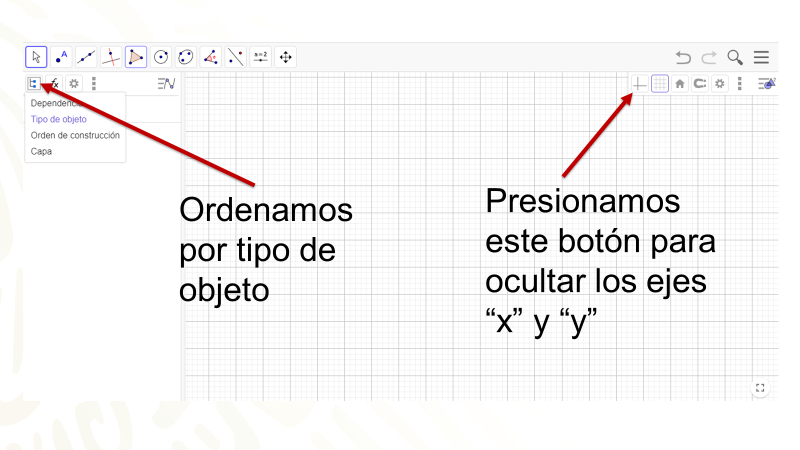
La configuración que conviene para la construcción de las Teselaciones es tener una vista gráfica, como se ve a continuación en la siguiente imagen, que tenga la cuadrícula, presiona el botón de ocultar los ejes “x” y “y”, necesitas que la vista gráfica ordene por tipo de objeto.
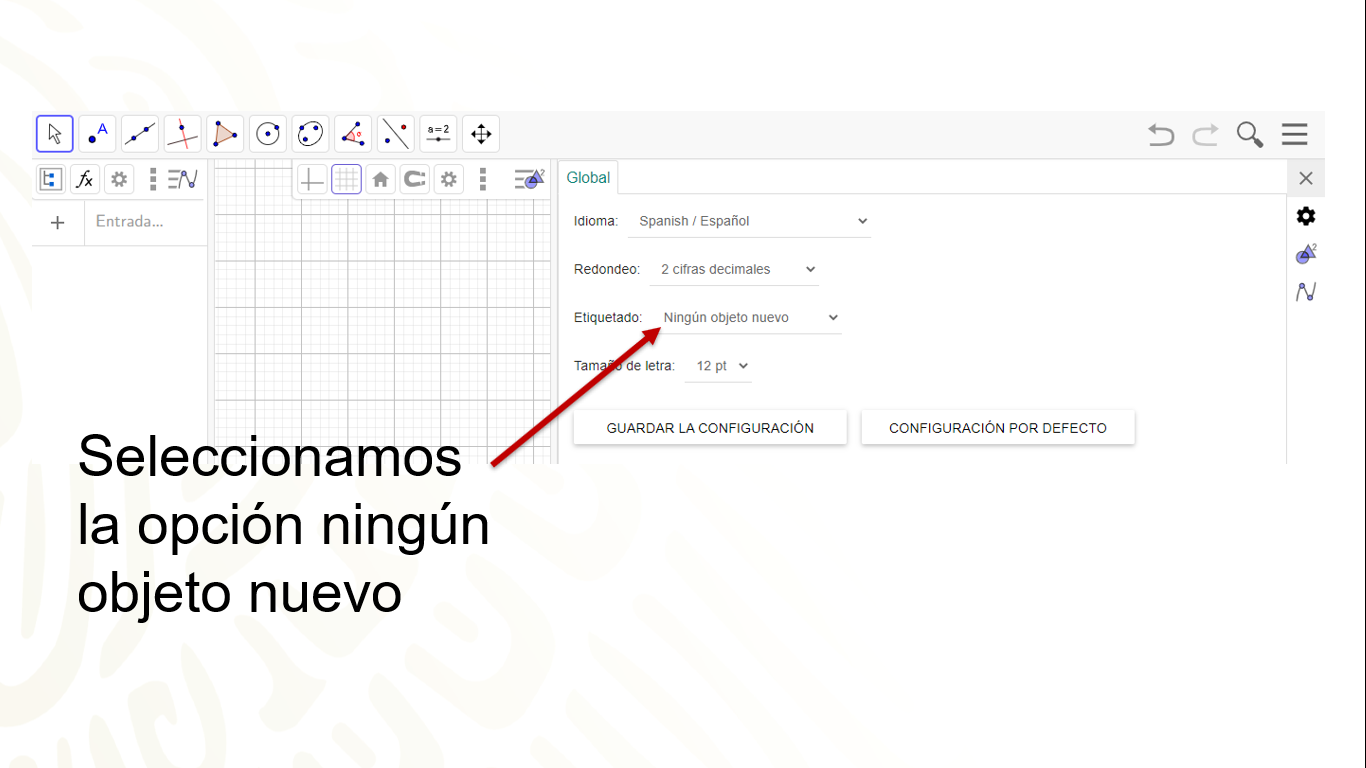
Presiona el botón de menú que se encuentra en la parte superior derecha, posteriormente seleccionas la opción propiedades.

Seleccionas la opción Ningún. Objeto nuevo guardas la configuración, si quieres seguir construyendo teselaciones.
Llevaras a cabo tu primera construcción en GeoGebra.
Actividad 1.
A partir de un hexágono regular construirás un mosaico en 3D. Revisa el siguiente video.
- Teselados 3D. Cubo.
https://youtu.be/QqtvWlEp5WM
(del min. 3.24 al 9.15)
Una marera de construir un teselado en 3D es la siguiente:
Selecciona la opción Polígono regular que se encuentra en la barra de herramientas; trazas una recta con una longitud de cuatro unidades y escribes el número 6 en la ventana que aparece. De esta manera construyes un hexágono regular.
Posteriormente, seleccionas la opción Segmento en la barra de herramientas y trazas tres segmentos uniendo vértices opuestos del hexágono como se muestra en el video.
Usas la opción Intersección en la barra de herramientas, para encontrar el centro del hexágono.
Luego, usarás la opción Polígono en la barra de herramientas, para marcar lo que será la cara izquierda de un cubo. Puedes escoger los colores que más te agraden para tu teselado.
Te ubicas dentro de la superficie de lo que será la cara del cubo; presionas el botón derecho del mouse y seleccionas la opción Configuración o Propiedades. Posteriormente, entras a la pestaña Color. En este caso, seleccionas el color gris oscuro número 32, con una opacidad del 100 y en la pestaña con el nombre Estilo, dejas en cero el grosor del trazo.
Haces el mismo procedimiento con la que será la cara superior del cubo. Te ubicas dentro de la superficie de la cara del cubo, presionas el botón derecho del mouse y seleccionas la opción Configuración; posteriormente, entras a la pestaña Color y, ahora, selecciona el color gris claro número 160, con una opacidad del 100 y en la pestaña de Estilo, el grosor del trazo lo dejarás en cero.
Para lo que será la cara inferior del cubo, te ubicas dentro de esa superficie, presionas el botón derecho del mouse y seleccionas la opción Configuración. Ahí, entras a la pestaña Color, y seleccionas el color gris número 96, con una opacidad del 100 y en la pestaña Estilo, el grosor del trazo lo dejarás en cero.
Luego, te ubicas en el vértice izquierdo de la cara gris oscuro y trazas un vector hacia el vértice superior derecho de la cara gris clara.
Ubicas un segundo vector del vértice izquierdo de la cara gris oscuro con número 32 hacía el vértice inferior derecho de la cara gris con el número 96.
Seleccionas el botón Elige y mueve para modificar los objetos en la vista algebraica. Así, pasas a la vista algebraica de la interfaz de GeoGebra. Para tu comodidad quitarás el polígono uno, los puntos A, B y G, también los segmentos “l”, “m” y “n”, presionando cada uno de los botones mencionados.
Ocultas los puntos C, D, E y F que te quedan de manera individual, presionando el botón derecho del mouse y, en la coordenada que quieres ocultar, seleccionas la paloma con fondo azul de Mostrar objetos.
Pasas a la barra de herramientas y seleccionas la opción Desplaza la gráfica para hacer de menor tamaño la figura inicial y que puedas desplazar la figura hacia el lado izquierdo de la interfaz, para trasladarla hacia arriba y a la derecha.
Una forma de trasladar este cubo es seleccionando la opción Traslación en la barra de herramientas. Presionas el botón izquierdo del mouse, construyes un cuadrilátero encerrando al cubo; después, seleccionas y presionas el vector con el sentido hacia arriba.
Llevarás a cabo este proceso 2 veces, encerrando todos los cubos con un cuadrilátero y presionando el vector con sentido hacia arriba. De la misma forma lo harás con el vector cuyo sentido es hacía abajo.
A continuación, te ubicas en la parte superior de la vista algebraica, moviendo la barra de desplazamiento vertical hasta arriba. Seleccionas polígono, punto, cuadrilátero, segmento, para comprimir todos los objetos. Seleccionas la palabra Vector con el botón izquierdo del mouse y tocas la parte sombreada con el botón derecho; eliges la opción Objeto visible para quitar los vectores en la vista gráfica.
Para terminar, presionas el botón de menú de la vista gráfica para quitar el cuadriculado y tener tu primera construcción de un teselado en 3D con ayuda de GeoGebra.
Ahora, vas a realizar otro teselado, en un plano.
Actividad 2.
Construirás la segunda teselación llamada la pajarita de Nazarí.
Para realizarla, revisa el siguiente video. - Teselado la pajarita de Nazarí.
https://youtu.be/QqtvWlEp5WM
(del min. 9.35 al 18.03)
Una forma de construir el teselado de la pajarita de Nazarí es la siguiente.
Vas a la barra de herramientas y seleccionas polígono regular, trazas una recta con una longitud de cuatro unidades, escribes el número 3 en la ventana que aparece.
Te diriges a la barra de herramientas opción punto medio y ubicas los puntos medios en los tres lados del triángulo, puedes empezar con cualquier vértice.
Posteriormente marcas 2 puntos medios más, los llamarás puntos medios secundarios, del punto medio de la base al vértice derecho y del vértice derecho al punto medio del lado derecho del triángulo.
Trazas dos segmentos uno del punto medio del lado derecho con el punto medio secundario inferior y el segundo segmento del punto medio inferior al punto medio secundario del lado derecho.
Marcas la intersección de los 2 segmentos, te diriges a la barra de herramientas y seleccionas la opción intersección, regresas a la figura y tocas los dos segmentos para ubicar la intersección.
Pasas a la barra de herramientas buscas la ventana circunferencia y seleccionas arco de circunferencia, tocas la intersección y el punto medio de la base con el vértice derecho del triángulo y trazas un arco.
Le darás un color diferente al arco, tocas el arco y presionas el botón derecho del mouse, seleccionas la opción configuración, posteriormente entras a la pestaña con el nombre de color, en este caso se seleccionará el color azul y en la pestaña con el nombre de estilo, el grosor del trazo se dejará en siete y la opacidad al 100. Tú en casa puedes seleccionar el color que más te guste.
Rotarás el arco 5 veces, seleccionas la herramienta de rotar alrededor de un punto, se rota alrededor del vértice derecho del triángulo, vas a rotar 60 grados en sentido horario, después rotarás el arco con el punto medio del lado derecho del triángulo 180 grados con un sentido antihorario, continuas con la rotación del arco con respecto al vértice superior del triángulo 60 grados en sentido horario, ahora rotarás el arco con el punto medio del lado izquierdo del triángulo 180 grados con un sentido antihorario y la quinta rotación la llevarás con 60 grados en sentido horario.
Necesitas quitar varios objetos en la figura para continuar de manera más sencilla tu teselación. Te diriges a la vista algebraica y presionas los siguientes botones para quitar los objetos, polígono 1, punto medio D, E, F, G y H, la intersección “i” y los segmentos j y k.
Una manera para poder seguir construyendo el teselado es rotar la primera figura con respecto al vértice superior, te vas a la barra de herramientas y seleccionas rotar alrededor de un punto, con el botón izquierdo del mouse realizas un cuadrado encerrando la figura inicial, presionas el vértice superior y en la ventana escribes 60 grados antihorario, te das cuenta que en la segunda figura no se roto el vértice inferior derecho, haces lo mismo, con el botón izquierdo del mouse realizas un cuadrado encerrando el vértice inferior derecho, presionas el vértice central y en la ventana escribes 60 grados antihorario, nuevamente encierras la segunda figura con el botón izquierdo del mouse, presionas el vértice central y en la ventana escribes 60 grados antihorario, haces lo mismo, con el botón izquierdo del mouse realizas un cuadrado encerrando las tres figuras, presionas el vértice central y en la ventana escribes 180 grados antihorario, hizo falta rotar un punto, por lo tanto con el botón izquierdo del mouse realizas un cuadrado encerrando el vértice superior derecho, presionas el vértice central y en la ventana escribes 60 grados antihorario. Listo ya tienes tu teselado con seis pajaritas de Nazarí.
Con ayuda de la herramienta desplaza gráfica, harás más pequeña la figura, ubicándola en la parte izquierda del interfaz de GeoGebra.
Es momento de trasladar la figura inicial, para ello trazarás tres vectores, te vas a la barra de herramientas y seleccionas la opción vector, te ubicas en el vértice izquierdo de tu figura y proyectas el primer vector hacia el vértice derecho, el segundo vector lo proyectas del punto superior izquierdo hacia el vértice inferior derecho, el tercer vector lo proyectas del punto inferior izquierdo hacia el vértice superior derecho.
Antes de trasladar vas a quitar varios objetos de la figura, por lo tanto, te diriges a la vista algebraica de la interfaz de GeoGebra, presionas los puntos A, B, B prima, B biprima, B triprima, B1 triprima y B1 biprima.
Una forma de trasladar este teselado es seleccionando la opción de traslación en la barra de herramientas, presionas el botón izquierdo del mouse, realizas un cuadrilátero encerrando tu figura inicial, después seleccionas y presionas el vector con el sentido hacia abajo, llevarás a cabo este proceso 2 veces, encerrando las dos figuras y presionando el vector con sentido hacia derecha, de la misma forma lo harás con el vector con el sentido hacia arriba.
Presionas el botón de menú de la vista gráfica para quitar el cuadriculado de la interfaz.
A continuación, te ubicas hasta la parte superior de la vista algebraica, presionas en el botón izquierdo de cónicas, punto, segmento, para comprimir los objetos.
Después, presionas la palabra vector con el botón izquierdo del mouse y tocas la parte sombreada con el botón derecho del mouse, presionas la opción objeto visible para quitar los vectores en la vista gráfica.
Para terminar, centras tu teselado la pajarita de Nazarí. Con esta actividad construiste el cuarto teselado con ayuda de GeoGebra.
Actividad 3.
Construirás la tercera teselación a partir de un cuadrado formando un mosaico propio.
Para ello, revisa el siguiente video. - Teselado propio 1.
https://youtu.be/QqtvWlEp5WM
(del min. 18.20 al 25.30)
Una forma de construir tu propio teselado a partir de un cuadrado es la siguiente.
Vas a la barra de herramientas y seleccionas Polígono regular, trazas una recta con una longitud de cuatro unidades, y anotas el número 4 en la ventana que aparece.
El siguiente paso es ubicar los puntos medios en los cuatro lados del cuadrado. En la barra de herramientas, seleccionas la opción Punto medio.
Ahora, vas a seleccionar la opción Punto que se encuentra en la barra de herramientas y ubicas un punto en la parte inferior e interior del cuadrado. Lo editarás cambiando el color azul por rojo; aunque también puedes escoger cualquier color, y le darás un nuevo nombre, lo llamarás PUNTO BASE, ya que más adelante es el que modificará el diseño de tu teselado, además, le quitarás la etiqueta; selecciona el PUNTO BASE con el botón derecho de mouse y con el izquierdo inhabilitas la Etiqueta.
El siguiente paso es hacer una serie de rotaciones del PUNTO BASE, con los puntos medios de los lados y los vértices del cuadrado, por lo tanto, seleccionas la opción Rotación en la barra de herramientas, y haces este movimiento del PUNTO BASE, con respecto a los puntos medios de los lados del cuadrado, en un giro de 180 grados en sentido antihorario. Y con respecto a los vértices del cuadrado, se rota 90 grados en sentido horario. Como recordatorio después de la primera rotación regresas al PUNTO BASE, de color azul o color que hayas asignado.
A continuación, seleccionas Polígono en la barra de herramientas para marcar tu primera figura. Inicias con el vértice inferior izquierdo, posteriormente con el PUNTO BASE interno, después, con el punto medio, sigues con el PUNTO BASE externo y llegas al vértice inferior derecho. Repites este procedimiento en los cuatro lados del cuadrado.
Por conveniencia, quitarás algunos objetos de la vista gráfica. Vas a la Vista algebraica y pulsas los siguientes objetos con el botón izquierdo del mouse: polígono 1, las tres bases primas, los puntos E, F, G, H e I, y los tres puntos i primas.
Ahora, le darás un color a tu figura. Para ello, te ubicarás dentro de la superficie, presiona el botón derecho del mouse y selecciona la opción Configuración. Posteriormente, entras a la pestaña Color, en este caso se seleccionará el color púrpura 128, con una opacidad del 100 y en la pestaña Estilo, el grosor del trazo lo dejarás en cero. Puedes seleccionar cualquier color.
Una forma para construir tu propio teselado es rotar tres veces la figura. Para ello, seleccionarás Rotación en la barra de herramientas y la rotarás tres veces con respecto al vértice superior derecho de la figura inicial, con un ángulo de 90 grados en sentido antihorario. Ahora, seleccionarás un color diferente para cada una de las figuras; colores que se seleccionarán serán amarillo, azul y verde.
Ya que tienes tu base para el teselado, proyectarás dos vectores. Seleccionas Vector en la barra de herramientas y desplazarás dos vectores; el primero del vértice inferior izquierdo al vértice inferior derecho y el segundo, del vértice inferior izquierdo al vértice superior izquierdo.
Antes de llevar a cabo las traslaciones, quitarás algunos objetos de la vista gráfica. Seleccionas el cursor de la barra de herramientas para disminuir el tamaño de tu teselado, presionas el botón izquierdo de polígono para comprimir los objetos; después, con el botón izquierdo del mouse seleccionas la palabra Puntos, de forma automática, sombreas el espacio de todos los puntos. Luego, con el botón derecho del mouse tocas la parte sombreada para inhabilitar todos los objetos con el botón izquierdo del mouse. Los puntos faltantes los quitarás de forma manual.
Una forma de trasladar este teselado es seleccionando la opción Traslación en la barra de herramientas; presionas el botón izquierdo del mouse y construyes un cuadrilátero encerrando el teselado; después, seleccionas y presionas el vector con el sentido hacia arriba. Repites este procedimiento con el vector de sentido hacia la derecha.
En la Vista algebraica buscas el PUNTO BASE del teselado y lo activas.
A continuación, en la Vista algebraica presionas la palabra Vector con el botón izquierdo del mouse y tocas la parte sombreada con el botón derecho; eliges la opción Objeto visible para quitar los vectores en la vista gráfica.
Para terminar, presionas el botón de menú de la Vista gráfica para quitar el cuadriculado de la interfaz y tener tu tercera construcción de un teselado propio con ayuda de GeoGebra. Cabe decir que, si mueves la ubicación del PUNTO BASE, tu teselado cambia de forma.
Actividad 4.
Construirás la cuarta teselación a partir de un triángulo equilátero formando un mosaico propio.
Para eso, revisa el siguiente video. - Teselado propio 2.
Una forma de construir tu propio teselado a partir de un triángulo equilátero es la siguiente.
Vas a la barra de herramientas y seleccionas Polígono regular; trazas una recta con una longitud de cuatro unidades, escribes el número 3 en la ventana que aparece.
El siguiente paso es ubicar los puntos medios en los tres lados del triángulo. Para ello, en la barra de herramientas seleccionas la opción Punto medio.
Ahora, seleccionarás la opción Punto que se encuentra en la barra de herramientas y ubicarás un punto en la parte inferior e interior del triángulo. Lo editarás cambiando el color azul por rojo, aunque puedes elegir cualquier color.
Le darás un nuevo nombre, así que lo llamarás PUNTO BASE, ya que más adelante es el que modificará el diseño del teselado, además, le quitarás la Etiqueta; seleccionas el PUNTO BASE con el botón derecho del mouse y con el izquierdo inhabilitas la Etiqueta.
El siguiente paso es hacer una serie de rotaciones del PUNTO BASE con los puntos medios y vértices del triángulo, por lo tanto, seleccionas la opción Rotación en la barra de herramientas. El PUNTO BASE con respecto a los puntos medios de los lados del triángulo, se rota 180 grados en sentido antihorario y con respecto a los vértices del triángulo, se rota 60 grados en sentido horario. Como recordatorio después de la primera rotación regresas al PUNTO BASE de color azul.
A continuación, seleccionarás Polígono en la barra de herramientas para marcar la primera figura. Inicias con el vértice inferior izquierdo, posteriormente con el PUNTO BASE interno, después con el punto medio, sigues con el PUNTO BASE externo y llegas al vértice inferior derecho. Haces este procedimiento en los tres lados.
Por conveniencia quitarás algunos objetos de la vista gráfica. Te ubicas en la Vista algebraica y pulsas los siguientes objetos con el botón izquierdo del mouse: polígono 1, el PUNTO BASE, las tres bases primas, D, E, F, G y el G prima.
Ahora, le darás un color a tu figura. Para ello, te ubicas dentro de la superficie, presionas el botón derecho del mouse y seleccionas la opción Configuración; posteriormente, ingresas a la pestaña Color, y en este caso seleccionarás el color amarillo, con una opacidad del 100 y en la pestaña Estilo, el grosor del trazo lo dejarás en cero. Cabe decir que se puede elegir cualquier otro color.
Una manera de continuar con la construcción de este teselado es la siguiente: rotarás cinco veces la figura; para ello, seleccionas Rotación en la barra de herramientas y la giras tres veces con respecto al vértice superior de la figura inicial con un ángulo de 60 grados en un sentido antihorario. Ahora, seleccionas un color diferente para cada una de las figuras, los colores que seleccionarás serán el rojo, azul, verde, púrpura y rosa.
Ya que tienes tu base para el teselado, proyectarás dos vectores, pero necesitarás los puntos medios de la figura, por lo tanto, debes activarlos en la herramienta Vista algebraica. Seleccionarás Vector en la barra de herramientas y proyectas dos vectores; el primer vector del punto medio de la figura rosa al punto medio de la figura azul y el segundo vector del punto medio de la figura púrpura al punto medio de la figura roja.
Antes de llevar a cabo las traslaciones, quitarás algunos puntos de la vista gráfica. Con el botón izquierdo del mouse seleccionas la palabra Puntos; de forma automática se sombrea el espacio de todos los objetos y con el botón derecho del mouse tocas la parte sombreada para inhabilitar todos los objetos con el botón izquierdo del mouse. El punto faltante lo quitarás de forma manual.
Una forma de trasladar este teselado es seleccionar la opción Traslación en la barra de herramientas. Luego, presionas el botón izquierdo del mouse, construyes un cuadrilátero encerrando el teselado. Después, seleccionas y presionas el vector con el sentido hacia arriba y repites este procedimiento con el vector de sentido hacia abajo.
A continuación, en la Vista algebraica presionas la palabra vector con el botón izquierdo del mouse y tocas la parte sombreada con el botón derecho; presionas la opción Objeto visible para quitar los vectores en la vista gráfica.
Presionarás el botón de menú de la Vista gráfica para quitar el cuadriculado de la interfaz y tener tu cuarta construcción de un teselado con ayuda de GeoGebra. En la vista algebraica buscas el PUNTO BASE de tu teselado y lo activas.
Te puedes dar cuenta que, si mueves la ubicación del PUNTO BASE, tu teselado cambia de forma.
Recuerda que lo que trabajaste en esta sesión, es una muestra de lo que se puede hacer con los teselados. Tú puedes explorar más formas de hacer teselados.
El reto de hoy:
Se te invita a construir y crear tus propias teselaciones con ayuda de GeoGebra.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion