Proporcionalidad inversa V

Proporcionalidad inversa V

Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: interpretar y resolver problemas que se modelan con este tipo de variación, incluyendo fenómenos de la economía.

¿Qué vamos a aprender?

En esta sesión interpretarás y resolverás situaciones de proporcionalidad inversa en contextos relacionados a la economía y áreas afines.

¿Qué hacemos?

Para iniciar analiza la tabla que se muestra a continuación. En ella aparecen datos relacionados con el tipo de cambio que presentó el dólar estadounidense en el último día de cotización del año, en diferentes años.

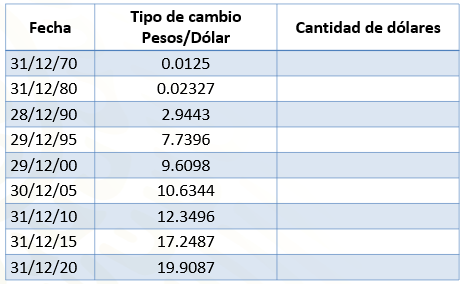
La primera columna corresponde a la fecha, la segunda columna muestra el tipo de cambio en relación pesos por dólar, por último, aparece la columna titulada cantidad de dólares.

Seguramente ya notaste que no hay datos en esa columna, por lo que deberás calcular la cantidad de dólares que se pueden comprar con 500 pesos de acuerdo con el tipo de cambio en cada fecha.

¿Qué operaciones sugieres plantear para poder calcular la cantidad de dólares que se pueden comprar con 500 pesos?

La operación que se puede plantear es el cociente de 500 pesos entre cada uno de los valores correspondientes al tipo de cambio, de esa manera, es posible saber la cantidad de dólares que podrían comprarse.

Por ejemplo, para saber cuántos dólares se pueden comprar con el tipo de cambio que existía en 1970, bastará con dividir 500 pesos entre 0.0125 pesos por dólar. Luego se realiza el análisis dimensional para simplificar unidades, que en este caso son los pesos; se resuelve la división y el cociente es igual a 40 000 dólares.

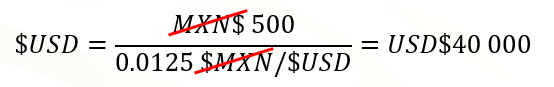
Recuerda que hubo un ajuste de 3 ceros en la década de los noventa, y el tipo de cambio varió de 3 000 pesos por dólar a 3 nuevos pesos por dólar.

Después repite el mismo procedimiento para los datos faltantes.

Para calcular la cantidad de dólares que se podían comprar con 500 pesos al tipo de cambio de 1980, se calcula el cociente de 500 pesos entre 0.02327 pesos por dólar.

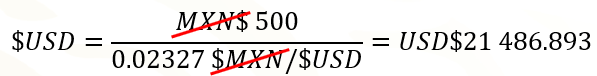
Repite el procedimiento hecho anteriormente para calcular los datos que aún faltan en la tabla, recuerda hacer el análisis dimensional para simplificar las unidades, es decir, simplificar las unidades de medida comunes que aparecen en el numerador y denominador de la expresión matemática.

Compara tus procedimientos y resultados con los que se muestran a continuación e identifica cuáles son las áreas que puedes mejorar.

El tipo de cambio el último día de cotización de 1990 fue de 2 punto 9 443 pesos por dólar, así que, con 500 pesos se podían comprar 169 punto 81 965 dólares.

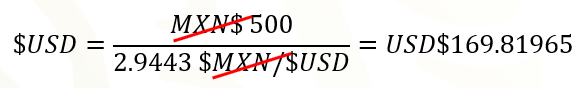
El último día de cotización del año 1995, se podían comprar 64 punto 6 028 dólares con 500 pesos.

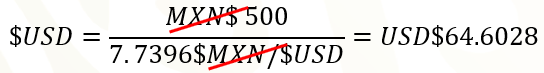
En el año 2000, el tipo de cambio del último día de cotización era de 9 punto 6 098 pesos por dólar y con 500 pesos alcanzaba para comprar 52 punto cero 30 dólares.

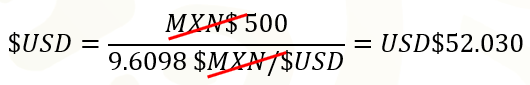
47 punto cero 17 dólares se podían comprar con 500 pesos el 30 de diciembre de 2005, pues el tipo de cambio estaba en 10 punto 6 344 pesos por dólar.

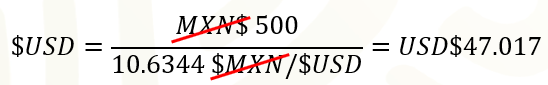
El tipo de cambio el último día del año 2010 fue de 12 punto 3 496 pesos por dólar, por lo, que con 500 pesos era posible comprar 40 punto 487 dólares.

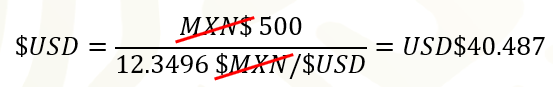
Para el último día del año 2015, con 500 pesos era posible comprar 28 punto 987 dólares, pues el tipo de cambio en ese entonces fue de 17 punto 2 487 pesos por dólar.

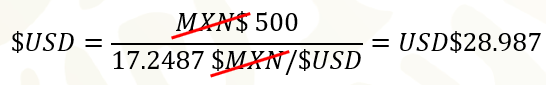
Por último, el 31 de diciembre de 2020, con un tipo de cambio de 19 punto 9 087 pesos por dólar, era posible comprar 25 punto 1 146 dólares.

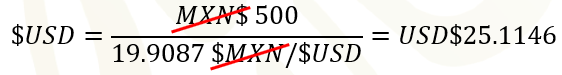
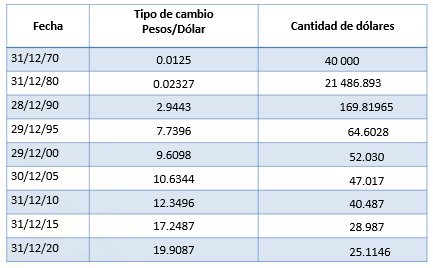
Toma unos instantes para analizar los datos que se muestran en la tabla. Después, en tu cuaderno, traza una gráfica que se represente en el eje “x” al tipo de cambio y en el eje “y” a la cantidad de dólares que se podían comprar. También piensa en las escalas que puedes considerar para representar los datos en el plano cartesiano.

A continuación, se muestra la gráfica que representa la cantidad de dólares que se pueden comprar en función del tipo de cambio en cada año.

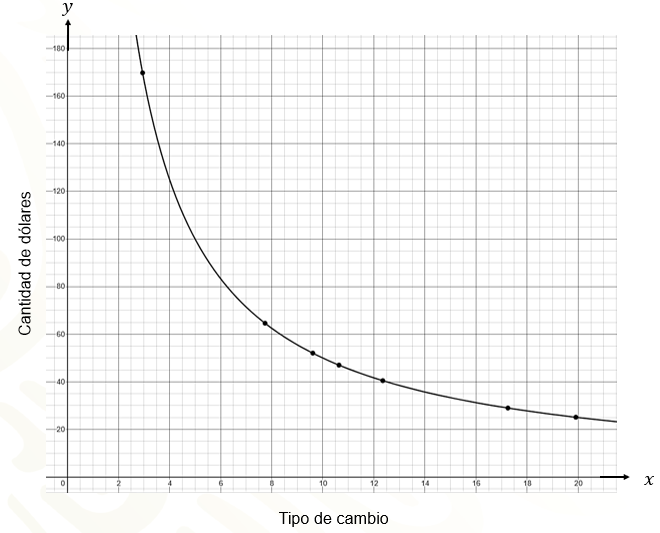
¿Qué forma tiene la línea que define la gráfica?

Esa línea curva recibe el nombre de hipérbola, Significa que los valores de las variables se pueden aproximar mucho al cero, pero jamás valdrán cero.

A partir de la gráfica y los datos de la tabla, responde las siguientes preguntas.

¿Qué sucede con la cantidad de dólares que se pueden comprar con 500 pesos conforme aumenta el tipo de cambio?

Conforme aumenta el tipo de cambio, la cantidad de dólares que se pueden comprar con 500 pesos disminuye.

Por ejemplo, tanto en la tabla como en la gráfica, se puede ver que cuando el tipo de cambio está en 2 punto 9 443 pesos por dólar en 1990 y aumenta aproximadamente 3 punto 6 veces en el año 2005 a 10 punto 6 344 pesos por dólar, sucede lo inverso en las cantidades correspondientes, es decir, la cantidad de dólares que se pueden comprar con 500 pesos disminuye en la misma proporción, de 169.81965 a 47.0 17 dólares.

Pon atención en la gráfica y escribe en tu cuaderno, ¿qué sucede con la cantidad de dólares que se pueden comprar a medida que aumenta el tipo de cambio?

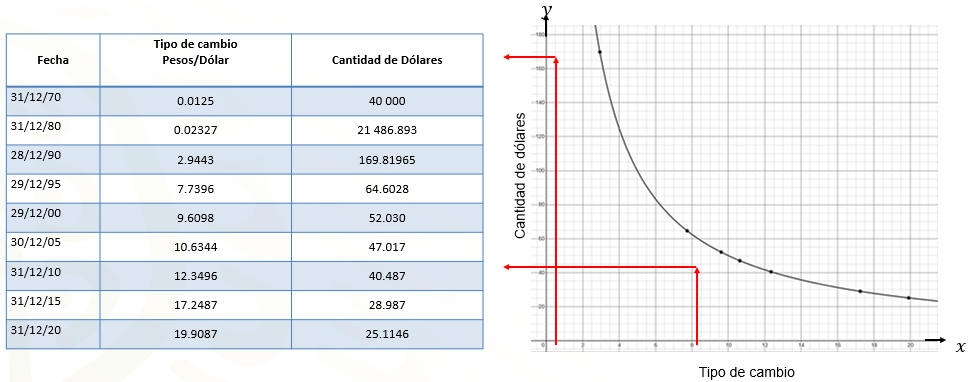
En la gráfica es visible que, mientras más dólares se pueden comprar, el precio por dólar en el tipo de cambio es más bajo.

Por ejemplo, cuando el punto de la gráfica está en el valor más alto en el eje “y” correspondiente a la cantidad de dólares, al mismo tiempo, se encuentra en el menor valor del eje “x” correspondiente al tipo de cambio.

En una situación hipotética, si el tipo de cambio fuera de un peso por dólar, se podrían comprar 500 dólares con 500 pesos.

En la gráfica que trazaste en tu cuaderno, marca las coordenadas correspondientes al dato anterior.

Hasta este momento, ya has resuelto una actividad que relaciona de manera específica dos cantidades. ¿Sabes de qué tipo de relación se trata?

Toma un momento para pensarlo y en tu cuaderno escribe tu respuesta y arguméntala. Después y a la distancia, compara tus argumentos con tus compañeras, compañeros, maestras y maestros.

Se trata de una relación de proporcionalidad inversa porque al aumentar los valores de una cantidad, los valores de la cantidad correspondiente disminuyen proporcionalmente. Por otro lado, al elaborar la gráfica de la situación planteada, la línea que la define es una hipérbola y en este tipo de gráficas se obtienen situaciones de proporcionalidad inversa y significa que los valores de las variables se pueden aproximar mucho al cero, pero jamás valdrán cero.

¿Qué otros argumentos escribiste? Compáralos e identifica las áreas en las que puedes mejorar.

Es momento de que resuelvas una nueva situación.

El bono semanal que un empleado recibe por su puntualidad es inversamente proporcional al número de minutos que llega tarde a su trabajo. El bono completo se otorga al empleado, aunque llegue tarde un minuto. A partir de ese tiempo se inicia el descuento y si acumula una hora de retardos, pierde el derecho al bono. ¿Cuál es la expresión algebraica que representa la situación?

En cierta semana, todos los empleados llegaron tarde a su trabajo, un empleado que llegó 5 minutos tarde recibió un bono de 250 pesos. ¿Cuánto recibirán de bono semanal los empleados que llegaron 10, 12, 15 y 50 minutos tarde?

Toma un momento para elaborar y escribir en tu cuaderno una estrategia que te permita responder a las preguntas planteadas. Después compara tu estrategia con la que se propone aquí y reflexiona sobre los puntos de acuerdo y desacuerdo.

El contador Antonio es el responsable de calcular el bono de puntualidad. Él sabe que, al tratarse de una relación de proporcionalidad inversa, la constante de proporcionalidad inversa se expresa a través del producto de sus magnitudes, en este caso, constante de proporcionalidad inversa es igual al tiempo que llega tarde el empleado en minutos por el bono semanal en pesos.

Si se definen algebraicamente las variables, tenemos que:

Con esta reflexión y análisis ya puedes responder a la primera pregunta.

Lo siguiente por hacer son los cálculos que permitirán al contador Antonio conocer el bono semanal de cada empleado.

Para continuar, se deben sustituir en la expresión algebraica los datos que se conocen y despejar, de ser necesario, a la variable desconocida.

Se sabe que “k” es igual a “x” por “y”. También se sabe que un empleado que llegó 5 minutos tarde recibió de bono mensual de 250 pesos. Entonces, al realizar la sustitución de datos se tiene que:

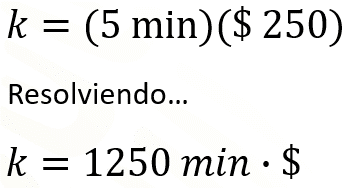
¿Qué utilidad tiene conocer el valor de la constante de proporcionalidad?

En tu cuaderno escribe una conclusión al respecto.

Conocer el valor de la constante de proporcionalidad, permitirá realizar los cálculos para conocer el bono semanal que ganará cada empleado en función de los minutos que llega tarde al trabajo.

Por ejemplo, para calcular el bono semanal del empleado que llegó 10 minutos tarde, se puede sustituir en la expresión algebraica anterior los valores conocidos. En este caso, se conoce el valor de "k" que es la constante de proporcionalidad y también se conoce el valor de "x" que son los minutos que llega tarde un empleado. Al sustituir los valores en la expresión algebraica se obtiene que:

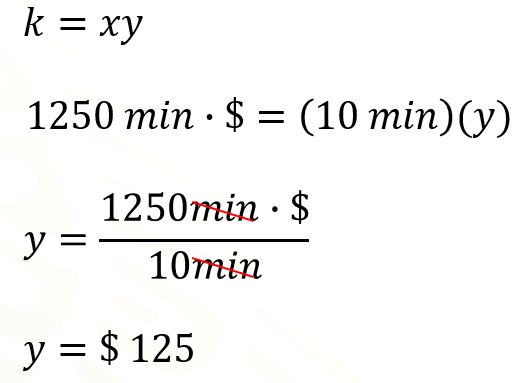
En otras palabras, el empleado que llegó 10 minutos tarde, recibió un bono semanal de 125 pesos.

Sigue en tu cuaderno el procedimiento que usó el contador Antonio para calcular el bono semanal de los empleados que faltan.

Ahora, compara procedimientos y tus respuestas con los que se muestran a continuación y corrige de ser necesario.

Para calcular el bono semanal de un empleado que llegó 12 minutos tarde, se sustituye en la fórmula a “x” y en su lugar se escriben 12 minutos.

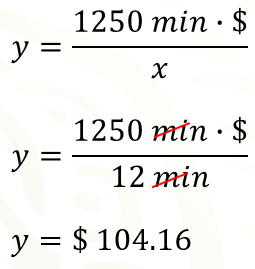
Es decir, el empleado que llegó 12 minutos tarde, recibió un bono de 104.16 pesos.

Se sigue el mismo procedimiento para calcular el bono del empleado que llegó 15 minutos tarde. Se sustituyen valores en la fórmula, se hace el análisis dimensional y se resuelve la división indicada.

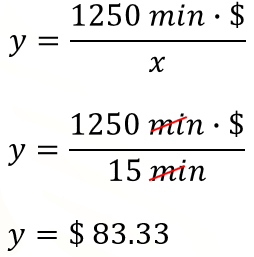
El cociente es igual a 83.33 pesos que representan el bono semanal de ese empleado.

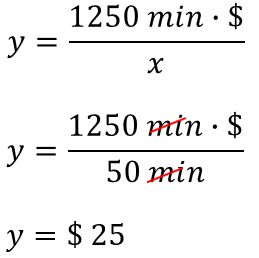
Por último, se determina que el empleado que llegó 50 minutos tarde, recibirá un bono semanal por 25 pesos.

Existen varias maneras de argumentar este resultado sin la necesidad de hacer los cálculos que se hicieron en el procedimiento anterior, una de ellas puede ser a través de la elaboración de la gráfica que modela la situación, pero también se pueden analizar las correspondencias entre las magnitudes, por ejemplo.

El empleado que llegó 5 minutos tarde, recibió un bono semanal de 250 pesos, mientras que el empleado que llego 50 minutos tarde, recibió un bono semanal de 25 pesos. ¿Cuántas veces aumentaron los minutos que llegó tarde el último empleado con respecto a los del primero? Aumentaron 10 veces.

¿Cuántas veces disminuyó el bono semanal que recibió el ultimo empleado en comparación con el primero?

El bono disminuyó 10 veces. Como ya notaste, mientras los minutos se incrementaron 10 veces, el bono disminuyó a una décima parte. Lo anterior, es una propiedad que define a las relaciones de proporcionalidad inversa.

Analiza y resuelve la siguiente situación.

Supón que el precio de un producto se reduce proporcionalmente conforme se incrementa su producción. ¿Cuánto costará una lámpara solar al producir 15 000 piezas, si su costo unitario es de 500 pesos cuando se producen 10 000 unidades?

¿Cuántas piezas deberán producirse para que el precio por lámpara solar sea de 250 pesos?

¿Será posible ofrecer una lámpara solar con valor unitario menor a 100 pesos si la capacidad máxima de producción de la fábrica es de 50 000 lámparas?

Elabora y escribe en tu cuaderno una estrategia para responder las preguntas planteadas.

Una estrategia de resolución puede ser la elaboración de una tabla de valores con los datos que se conocen, y a partir de ahí, calcular los valores faltantes.

Construye una tabla con dos columnas y tantas filas como sean necesarias. En una columna escribe todos los valores que correspondan al número de lámparas que produce la fábrica y puedes titularla como producción de lámparas. En la otra columna, escribe los costos unitarios correspondientes a cada producción de lámparas, esa columna la puedes titular como precio o costo por lámpara.

¿Ya tienes construida tu tabla? Compárala con la que a continuación se muestra, identifica puntos en común y diferencias, y de ser necesario, revisa tu procedimiento y corrige.

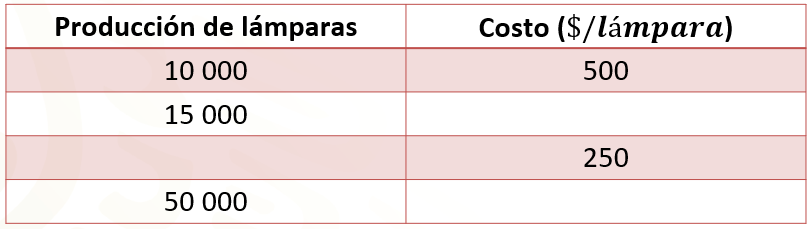
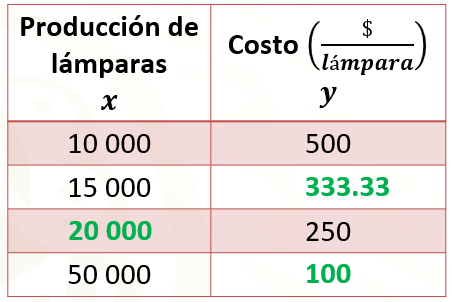
La tabla tiene los datos que proporciona el problema, por ejemplo, la primera pareja de datos corresponde a la situación inicial, donde el costo es de 500 pesos por lámpara cuando la producción es de 10 000 lámparas.

El siguiente dato que se muestra en la columna correspondiente a la producción de lámparas, se obtuvo de la primera pregunta que solicita el costo de una lámpara cuando hay una producción de 15 000 lámparas. Por otro lado, el tercer dato de la columna correspondiente al costo, se obtuvo de la segunda pregunta que requiere conocer la producción de lámparas para tener un costo de 250 pesos por cada una.

Por último, el cuarto dato correspondiente a la producción de lámparas, se obtuvo de la tercera pregunta que indica la capacidad máxima de producción de la fábrica.

¿Ideaste una estrategia para obtener los valores faltantes?

Como se trata de una relación de proporcionalidad inversa, se sabe que la constante de proporcionalidad “k” es igual al producto de sus magnitudes que se corresponden, es decir, “k” es igual a “x” por “y”. Si se considera a la producción de lámparas solares como los valores de “x” y el costo unitario como los valores de “y”, entonces se tiene que al conocer “x” igual a

10 000 y “y” igual a 500, entonces “k” es igual a 10 000 por 500, de donde se obtiene que “k” es igual a 5 millones.

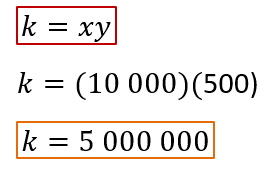
Con este dato puedes calcular los valores faltantes en la tabla, pero antes, habrá que despejar a “x” y a “y”.

Al aplicar las propiedades de la igualdad, se obtiene que:

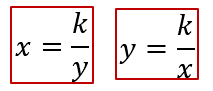
Ya cuentas con todos los elementos para calcular los valores faltantes de la tabla.

Para saber el costo de una lámpara solar cuando la fábrica tiene una producción de 15 000 lámparas solares, se utiliza la expresión algebraica “y” es igual a “k” entre “x”; se sustituyen los valores, entonces:

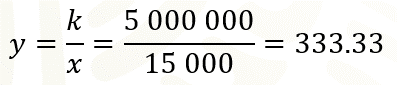
El cociente es igual a 333.33 pesos por cada lámpara solar.

La fórmula “x” es igual a “k” entre “y” se utiliza para saber la producción de lámparas que se necesitan para que cada una tenga un costo de 250 pesos. Al sustituir los valores queda indicada la división.

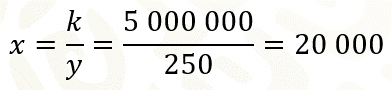
Por último, se calcula el costo cuando la producción de lámparas es de 50 000. Para ello, se usa la fórmula “y” es igual a “k” entre “x”. Se sustituyen los valores, se resuelven las operaciones.

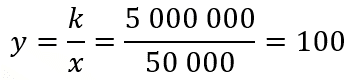
Con todos los datos en la tabla, ya es posible responder a las preguntas planteadas. Escribe tus respuestas en el cuaderno.

¿Cuánto costará una lámpara solar al producir 15 000 piezas, si su costo unitario es de 500 pesos cuando se producen 10 000 unidades?

De acuerdo con los datos de la tabla, si se producen 15 000 piezas, el costo de cada lámpara solar será de 333.33 pesos.

Para la pregunta, ¿cuántas piezas deberán producirse para que el precio por lámpara solar sea de 250 pesos?

Según la información de la tabla, se deberán producir 20 000 lámparas solares para garantizar que el costo sea de 250 pesos.

La tercera pregunta dice ¿será posible ofrecer una lámpara solar con valor unitario menor a 100 pesos si la capacidad máxima de producción de la fábrica es de 50 000 lámparas?

En la tabla se puede ver que el costo de cada lámpara cuando la fábrica produce a su máxima capacidad es de 100 pesos, por lo tanto, no es posible ofrecer una lámpara solar con un valor unitario menor a 100 pesos. Para ello, se requiere de producir más de 50 000 lámparas solares, lo que sobrepasaría la capacidad máxima de producción de la fábrica.

Cabe aclarar que esta situación sería factible sólo si el costo de producción de las lámparas solares es mucho menor a 100 pesos, para que siempre se tenga una utilidad al venderlas con un precio mínimo de 100 pesos.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html