Método de igualación

Método de igualación

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: resolver problemas mediante el planteamiento y la solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de igualación.

¿Qué vamos a aprender?

Profundizarás en el estudio de la resolución de sistemas de ecuaciones lineales con 2 incógnitas.

Los materiales que necesitarás es tu cuaderno o algunas hojas de papel, lápiz, goma, sacapuntas y bolígrafos para hacer tus anotaciones.

Es necesario que registres las reflexiones e ideas que concretes con las explicaciones que aquí desarrollarás.

Además, escribe tus dudas y dificultades, las cuales puedes consultar con tu profesor.

Desde que ibas en primaria, has estudiado los distintos algoritmos para resolver operaciones, así mismo, has transitado de operaciones aritméticas a operaciones algebraicas, logrando comprender una situación problemática para modelarla y encontrar su solución.

Ahora puedes resolver ecuaciones lineales, las cuales usarás para formar un sistema de ecuaciones de 2 por 2.

¿Qué hacemos?

Un sistema de ecuaciones lineales de dos por dos está formado por dos ecuaciones con dos incógnitas distintas entre sí, pero el valor de cada incógnita en ambas ecuaciones es igual.

Por ejemplo, en la siguiente imagen se observa la primera ecuación con dos incógnitas distintas entre sí, “y” igual a 8 “x” más 2.

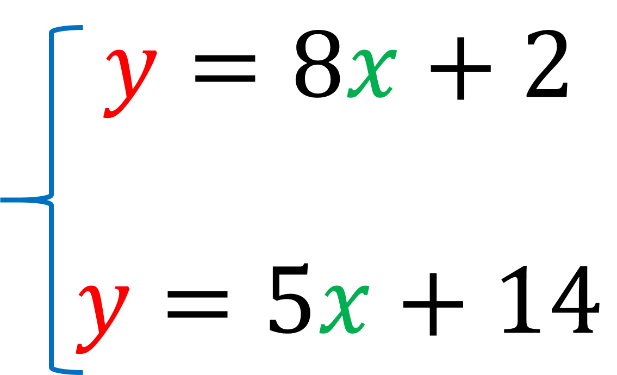
Y la segunda ecuación “y” igual a 5 “x” más 14.

También tienen dos incógnitas distintas entre sí, pero al ser parte del mismo sistema de dos por dos, el valor de x en ambas ecuaciones es el mismo. De la misma forma el valor de “y” en ambas ecuaciones es igual.

Las ecuaciones pueden ser la modelación de un problema o de una situación en la cual desconoces los valores de las incógnitas.

Analiza el siguiente ejemplo:

Es probable que puedas resolver este problema de múltiples maneras. Puedes suponer valores e ir haciendo cálculos que te aproxime a la respuesta, hasta que, después de varios intentos, encuentres aquellos que cumplen con las condiciones del problema.

En esta ocasión lo resolverás usando álgebra, específicamente el método de igualación y lo primero que harás será modelar el problema con un sistema de ecuaciones.

Para ello, puedes identificar los datos necesarios para modelar la primera ecuación.

Lee nuevamente los enunciados del problema y responde: ¿Qué datos recuperas para modelar la primera ecuación?

El 76% de los alumnos y el 55% de las alumnas los cuales dan un total de 30 personas que aprobaron matemáticas.

Debido a que desconoces la cantidad de alumnos y alumnas, la representarás con alguna literal con la cual sea más fácil interpretar el problema y la solución, en este caso elegirás la “h” y la “m” para representar la cantidad desconocida de hombres y mujeres.

La “h” no representa a los hombres como género, ésta representa la cantidad de alumnos que hay en el grupo, así como la “m” no representa a las mujeres como género, ésta representa la cantidad de ellas que hay en el grupo.

Una vez que ha hecho énfasis en ello, construye el modelo con una ecuación.

En esta ocasión, trabajarás con los porcentajes en su representación decimal. Por lo tanto, la primera ecuación queda de la siguiente manera:

Analiza la ecuación y contesta:

¿Por qué elegiste trabajar con la representación decimal de los porcentajes?

¿Qué significa el cero punto 76 “h” y el cero punto 55 “m”?

¿Por qué es igual a 30?

Modela la segunda ecuación. ¿Qué datos serán la referencia para modelarla?

El 60% de los alumnos y el 80% de las alumnas que dan un total de 31 personas aprobados en la asignatura de español.

La segunda ecuación que con la cual modelarás los datos que faltaban del problema, es la siguiente:

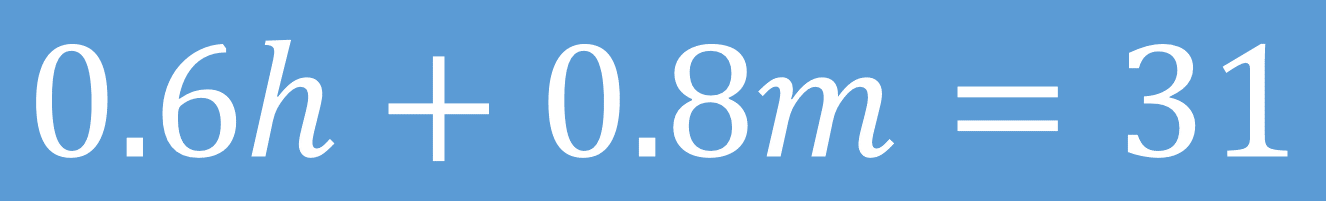
Analiza la ecuación planteada y responde las siguientes preguntas:

¿Qué significan el 0 punto 6 “h” y cero punto 8 “m”?

¿Por qué la suma es igual a 31?

Las dos ecuaciones que se plantean forman parte de un sistema de ecuaciones lineales de 2 por 2, el cual resolverás por el método de igualación.

Para iniciar, elige alguna incógnita, la cual despejarás en ambas ecuaciones, debe ser la misma incógnita. Las características del sistema que se forman hacen que sean los mismos pasos para despejar las incógnitas en cualquiera de las ecuaciones.

En palabras “coloquiales”, está igual de difícil o igual de fácil, despejar cualquiera de las dos incógnitas.

Como no presenta mayor dificultad elegir una sobre la otra, despeja a “m”.

Para despejar a “m” en la primera ecuación, harás uso de las propiedades de la igualdad, por lo tanto, restarás cero punto 76 “h” en ambos miembros de la igualdad.

Al reducir términos semejantes obtienes:

Cero punto 55 “m” igual a 30 menos cero punto 76 “h”.

Divide toda la ecuación entre cero punto 55 para tener uno como coeficiente de “m”.

Al simplificar obtienes uno “m” igual a 30 menos cero punto 76 “h”, entre cero punto 55.

Como puedes observar, la “m” ha quedado despejada y aunque aún no sabes con certeza el resultado de las operaciones que están del lado derecho de la igualdad, la literal “m” ya está diciendo su valor:

“m” vale 30 menos cero punto 76 “h”, todo entre cero punto 55.

Realiza el mismo procedimiento con la segunda ecuación, para despejar también “m”.

Resta cero punto 6 “h” en ambos lados de la igualdad.

Al reducir términos semejantes obtienes cero punto 8 ”m” igual a 31 menos cero punto 6 “h”.

Divide ambos miembros de la igualdad entre cero punto ocho. Por lo que tienes cero punto 8 ”m” entre cero punto 8 igual a 31 menos cero punto 6 “h”, entre cero punto 8.

Luego, al simplificar tienes uno “m” igual a 31 menos cero punto 6 “h”, todo entre cero punto 8.

Como puedes observar, la “m” ha quedado despejada y aunque aún no sabes con certeza el resultado de las operaciones que están del lado derecho de la igualdad, aquí también la literal “m” ya está diciendo su valor:

“m” es igual a 31 menos cero punto 6 “h”, entre cero punto 8.

Observa y analiza el despeje de la primera ecuación y el de la segunda ecuación, ¿se ven iguales? ¿Acaso encuentras dos valores distintos de “m”?

No se encuentran valores distintos y, aunque las operaciones que se obtienen en el lado derecho de la igualdad en ambos despejes son distintos, obtendrás el mismo valor.

¿A qué piensas que se debe lo anterior?

Como en ambos casos se despejó la misma incógnita, es decir “m”, entonces las expresiones obtenidas en cada despeje forman una igualdad.

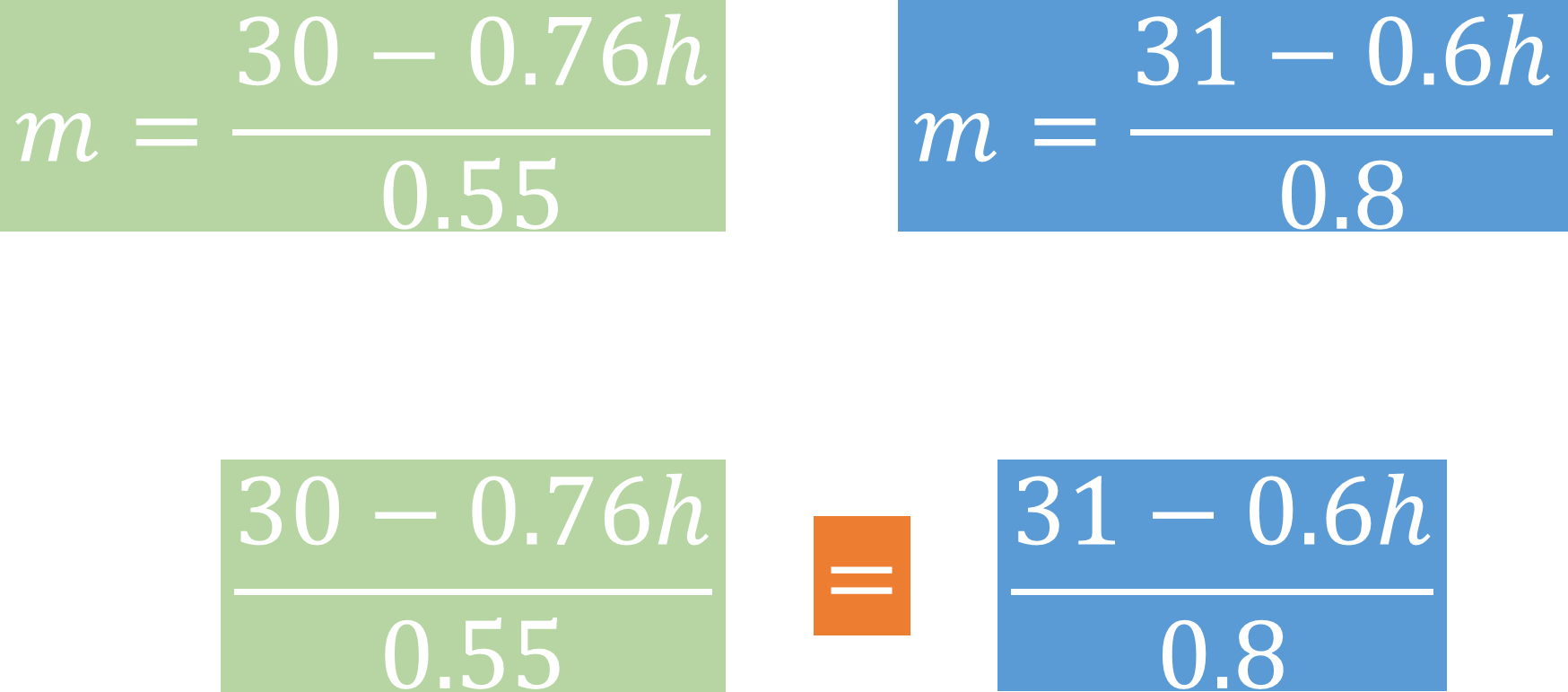
Observa atentamente y notarás que, de un sistema de dos por dos, pasas a un sistema de uno por uno, es decir, una ecuación con la misma incógnita en ambos miembros de la igualdad.

Esta nueva ecuación es 30 menos cero punto 76 “h”, entre cero punto 55 igual a 31 menos cero punto 6 “h”, entre cero punto 8.

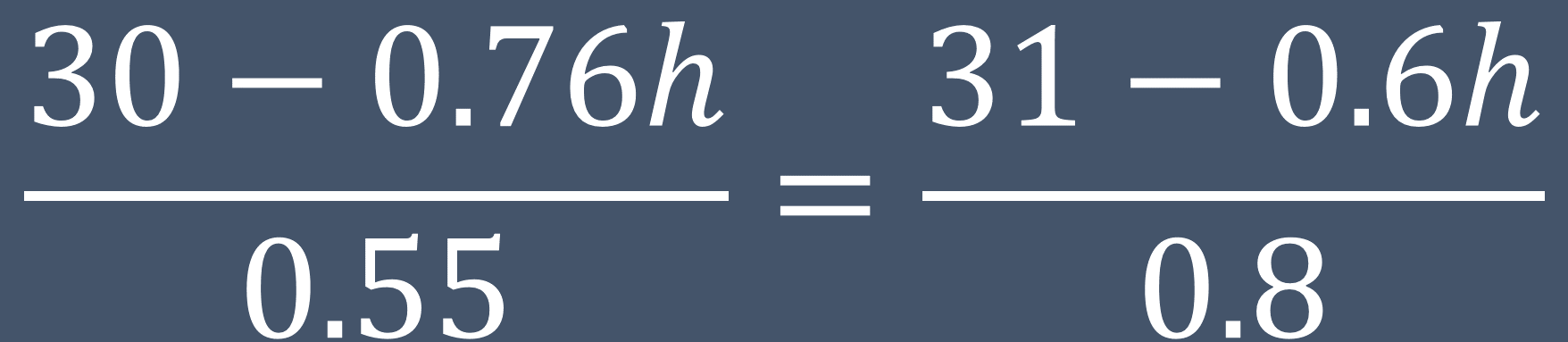
Para resolverlo puedes seguir el método que más domines, aquí usarás las propiedades de la igualdad para despejar a la incógnita.

Multiplica ambos lados de la ecuación por cero, punto 8 y también por cero punto 55, que son los denominadores de las expresiones obtenidas en el despeje de “m”.

¿Por qué multiplicas ambos miembros de la igualdad por estas cantidades?

Observa lo siguiente para contestar esta pregunta.

Al hacer estas multiplicaciones obtienes la cadena de operaciones que se muestra.

En ambos lados de la igualdad tienes tres factores en el numerador y uno en el denominador, y en ambos puedes simplificar.

Del lado izquierdo, puedes simplificar el cero punto 55 del numerador con el cero punto 55 del denominador y en el lado derecho el cero punto 8 del numerador con el cero punto 8 del denominador.

Obteniendo con ello la igualdad de dos factores.

Del lado izquierdo de la igualdad hay una multiplicación de cero punto 8 por 30 menos cero punto 76 “h” y del lado derecho, la multiplicación de 31 menos cero punto 6 “h” por cero punto 55, que puedes resolver de la siguiente manera.

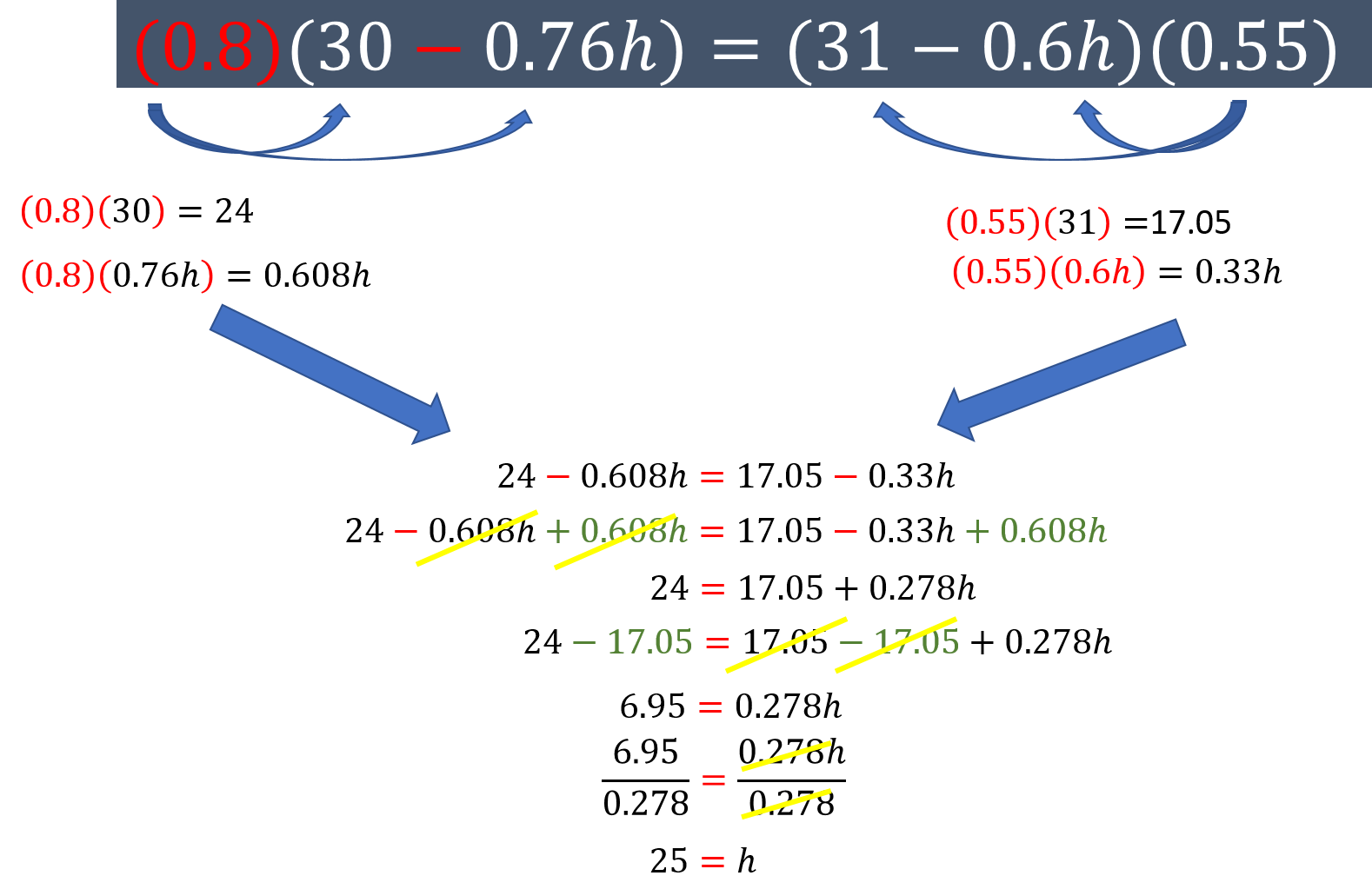
Aplicando la propiedad distributiva de la multiplicación con respecto a la resta, multiplicas cero punto 8 por 30 igual a 24, menos, cero punto 8 por cero punto 76 “h” que es igual a cero punto 608 “h”. Del otro lado de la igualdad multiplicas cero punto 55 por 31 igual a 17 punto cero 5, menos, cero punto 55 por cero punto 6 “h” que es igual a cero punto 33 “h”.

Al igualar los resultados anteriores se forma la ecuación 24 menos cero punto 608 “h” igual a 17 punto cero 5 menos cero punto 33 “h”.

Ahora, suma en ambos miembros de la igualdad cero punto 608 “h” y reduces términos semejantes, por lo que obtienes 24 igual a 17 punto cero 5 más cero punto 278 “h”.

Si restas en ambos lados de la igualdad 17 punto cero 5 y simplificas términos semejantes obtienes 6 punto 95 igual a cero punto 278 “h”.

Al dividir ambos miembros de la ecuación entre cero punto 278 y simplificas obtienes el valor de “h”, que es igual a 25.

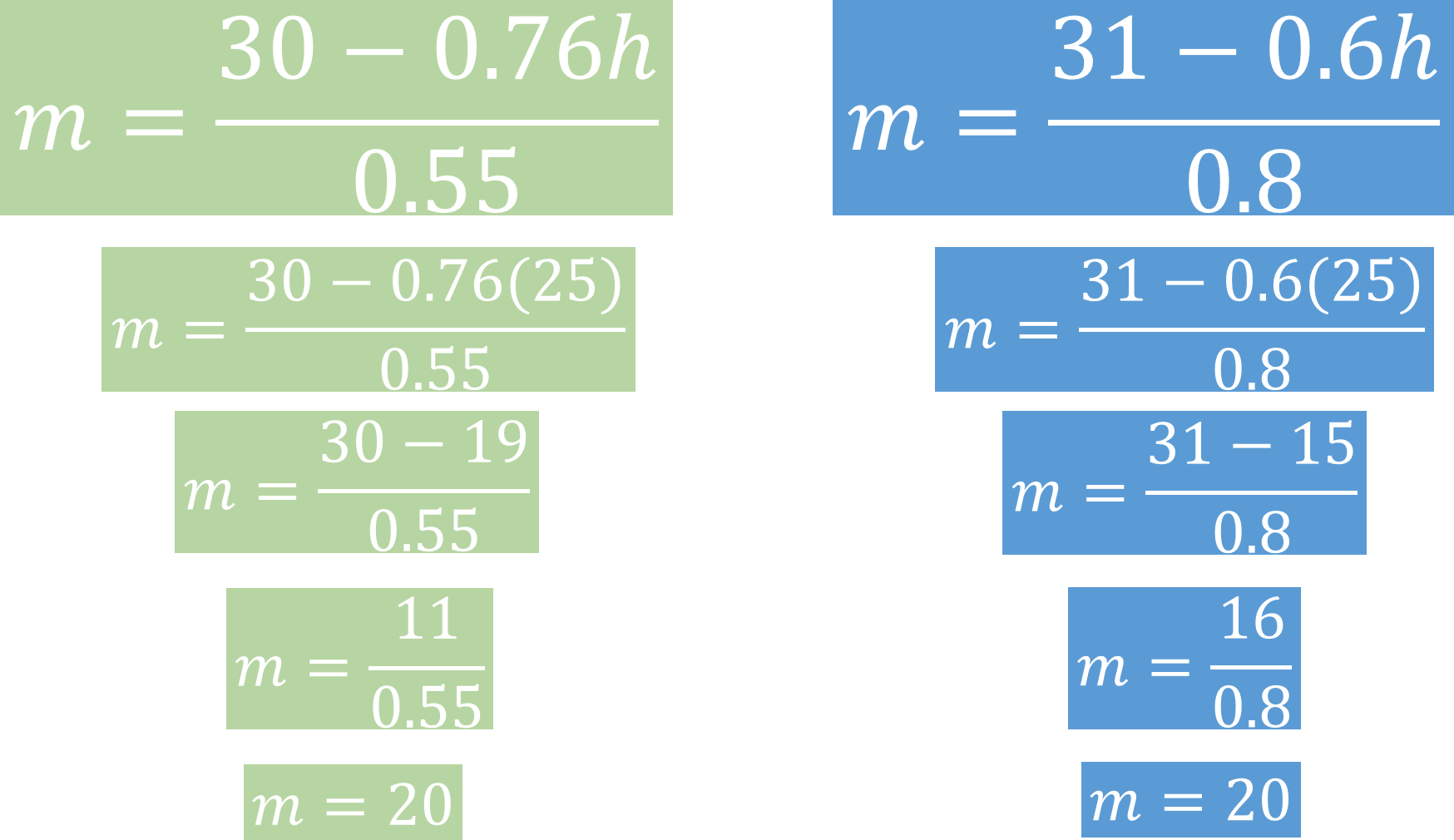
¿Qué significa 25 igual a “h” en el contexto del problema?

Significa que hay 25 alumnos varones en el grupo.

Aun debes obtener la cantidad de alumnas del grupo y para ello sustituirás el valor de los alumnos que acabas de calcular en cualquiera de los despejes que hiciste al inicio, en donde despejas “m”.

En esta ocasión sustituirás en los dos, para que observes que se cumple la igualdad, en cualquier caso.

En los despejes que realizas al inicio “m” es igual a 30 menos cero punto 76 “h” entre cero punto 55 y por otra parte “m” es igual a 31 menos cero punto 6 “h” entre cero punto 8.

Recuerdas que cuando se realizan esos despejes no importa que esas operaciones sean diferentes El valor de “m” es el mismo, verifícalo.

Ya que conoces el valor de “h” igual a 25, sustituirás ese valor en ambos despejes y resuelves las operaciones.

Para la primera ecuación “m” igual a 30 menos cero punto 76 por 25, entre cero punto 55 y para la segunda ecuación, “m” igual a 31 menos cero punto 6 por 25, entre cero punto 8.

Al resolver las multiplicaciones se obtiene en la primera ecuación “m” igual a 30 menos 19, entre cero punto 55 y para la segunda ecuación, “m” igual a 31 menos 15, entre cero punto 8.

Resolviendo las sustracciones se obtiene “m” igual a 11 entre cero punto 55 en la primera ecuación y “m” igual a 16 entre cero punto 8.

Obtienes el cociente de once entre cero punto 55 que es igual a 20 y 16 entre cero punto 8 que también es igual a 20.

Con esto puedes observar que en ambos casos “m” es igual a 20.

¿Qué significa esto en el contexto del problema?

Que el valor de “m” es igual a 20, por lo tanto, tienes un grupo con 25 alumnos y 20 alumnas.

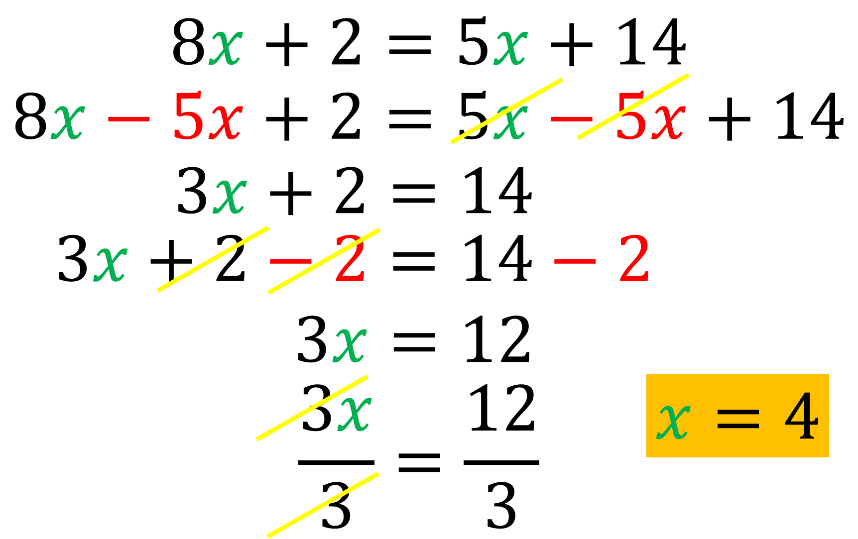
Al inicio de esta sesión, se presentó un ejemplo de un sistema de ecuaciones, ¿lo recuerdas?

El sistema está formado por la primera ecuación “y” igual a 8 “x” más 2 y la segunda ecuación, “y” igual a 5 “x” más 14.

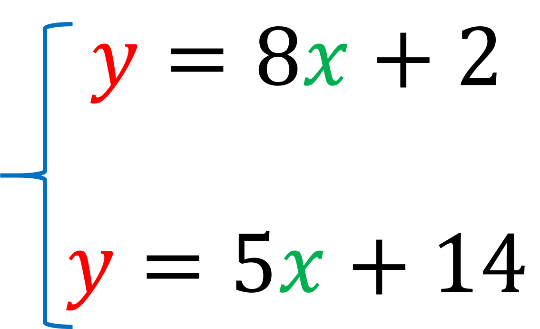
Aunque posteriormente estudiarás más métodos para resolver sistemas de ecuaciones, puedes observar que en este caso puede ser más conveniente usar el método de igualación que acabas de estudiar.

¿Por qué piensas que es más conveniente usar el método de igualación para resolver este sistema?

Porque ya está despejada la misma incógnita en ambas ecuaciones.

Al estar despejada la misma incógnita, igualarás las expresiones que son igual a “y”. Lo que resulta:

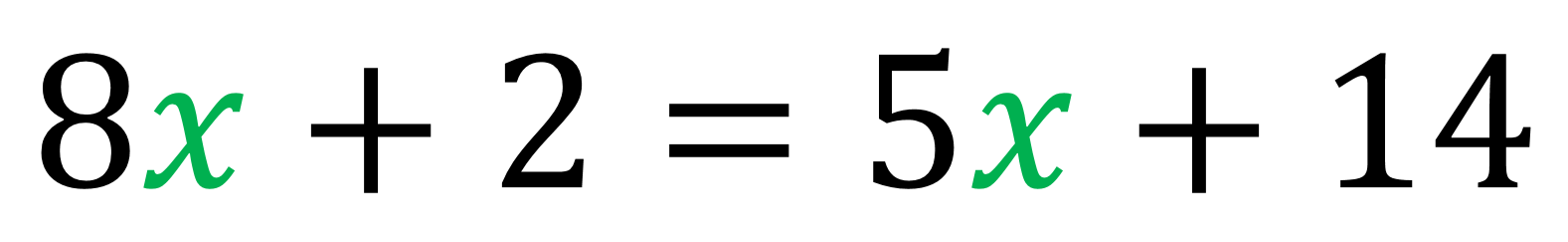
Al igual que cuando resuelves el sistema anterior, pasas de un sistema de dos ecuaciones con dos incógnitas a un sistema de una ecuación con una incógnita, y si despejas esa incógnita puedes conocer su valor.

Para resolver esta ecuación harás uso de las propiedades de la igualdad y comenzarás restando 5 “x” en ambos lados de la igualdad.

Lo que resulta 8 “x” menos 5 “x”, más 2 igual a 5 “x” menos 5 “x”, más 14. Al reducir términos semejantes resulta 3 “x” más 2 igual a 14.

Posteriormente, restas 2 en ambos lados de la igualdad, y al reducir términos semejantes obtienes 3 “x” igual a 12.

Ahora, divide ambos lados de la igualdad entre 3 y al simplificar obtienes el valor de “x” igual a 4.

Ya conoces el valor de una incógnita. Piensa ¿qué debes hacer para conocer el valor de la segunda incógnita?

Sustituir este valor en cualquiera de los despejes iniciales.

Como el sistema de inicio ya estaba despejado puedes sustituir el valor que acabas de calcular en cualquiera de las ecuaciones. Nuevamente sustituirás en ambas para comprobar que se cumple la igualdad.

Tanto en la ecuación “y” igual a 8 “x” más 2, como en “y” igual a 5 “x” más 14, sustituyes el valor de “x” por 4.

La primera ecuación ahora es “y” igual a 8 por 4, más 2 y la segunda, “y” igual a 5 por 4, más 14.

Resuelve las multiplicaciones y la primera ecuación ahora es “y” igual a 32 más 2 y la segunda es “y” igual a 20 más 14.

Resuelves las adiciones y obtienes el valor de “y”, que en ambas ecuaciones es 34.

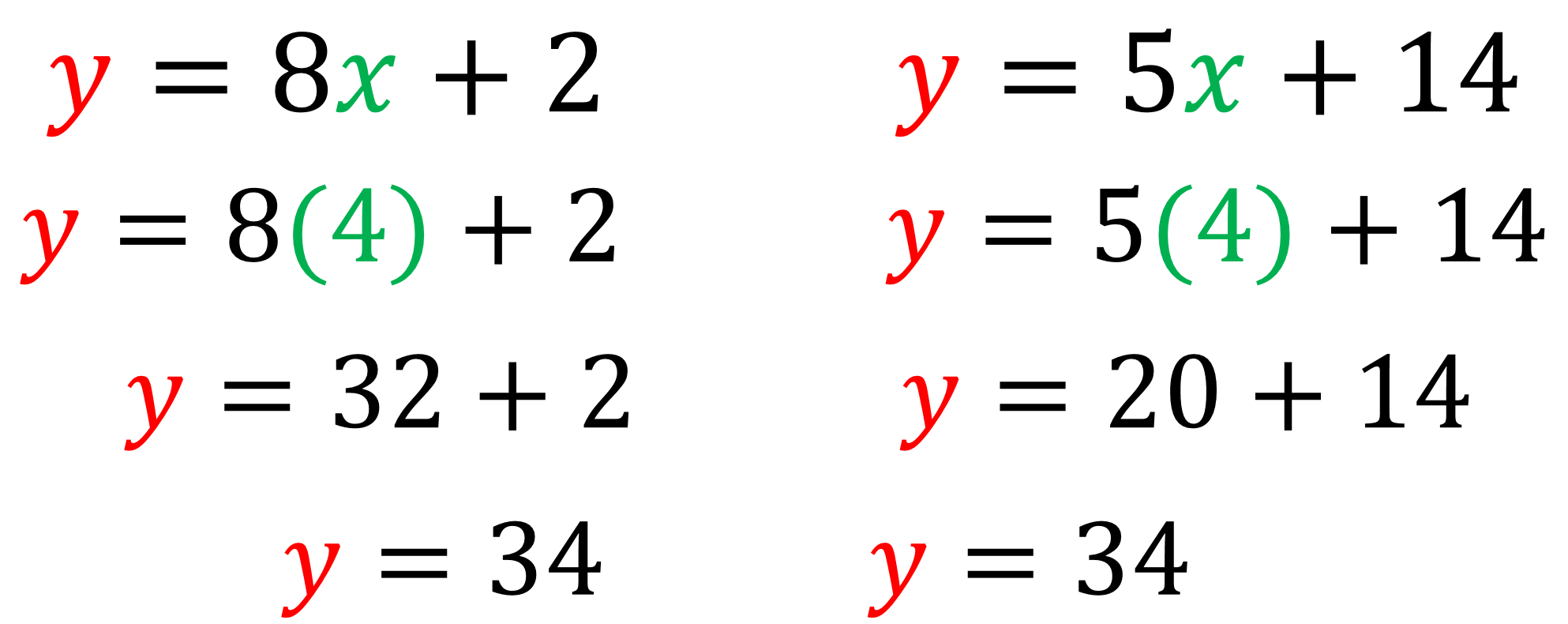
Por último, resuelve el siguiente sistema, también usando el método de igualación.

La primera ecuación del sistema es 2 “x” más 5 “y” igual a 145 y la segunda ecuación es 6 “x” más “y” igual a 113.

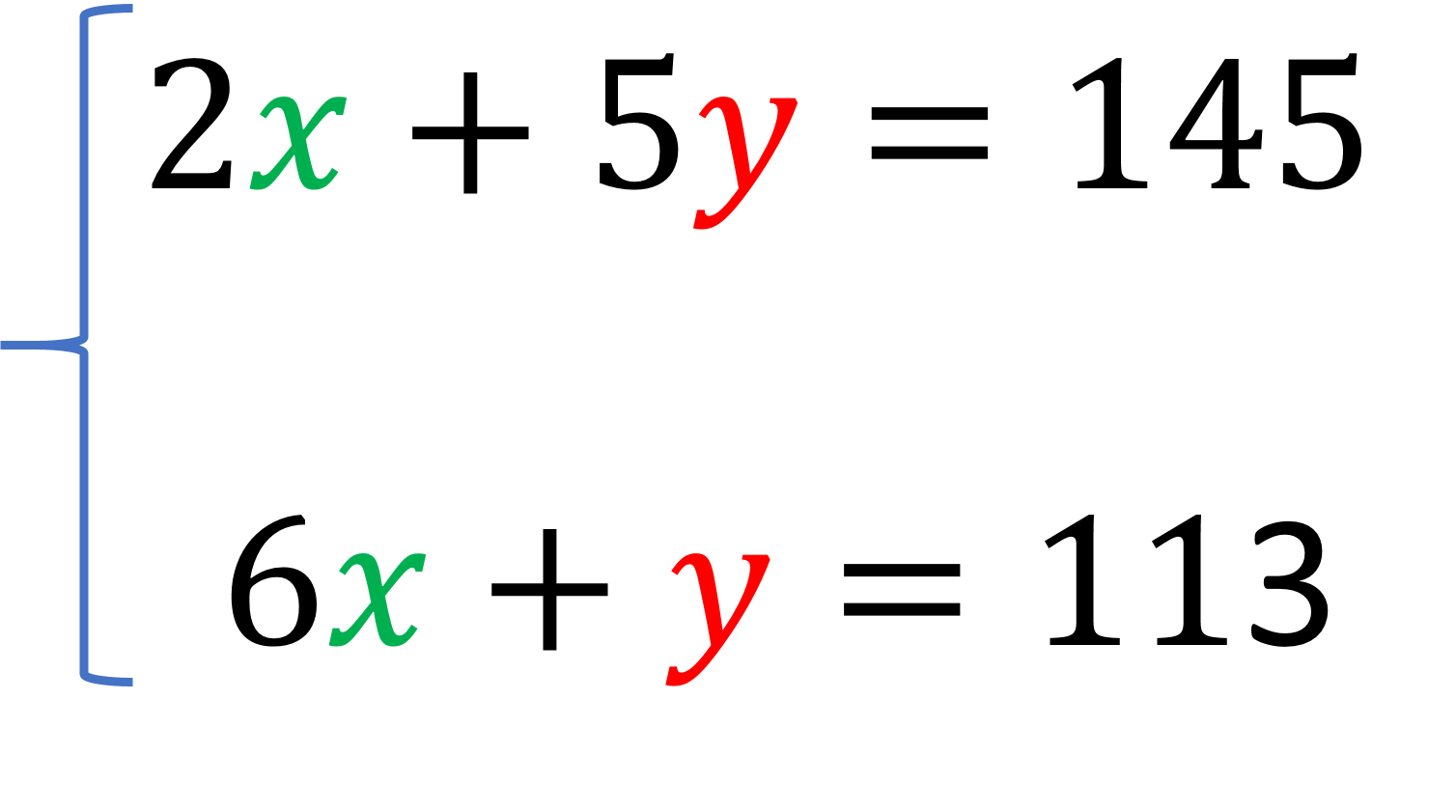
Analiza el sistema y responde ¿qué incógnita conviene despejar?

Como seguramente notaste, conviene despejar “y” en ambas ecuaciones, ya que en la segunda ecuación “y” ya tiene el coeficiente “uno” que, al no escribirse, ahorra pasos en el despeje.

Para el despeje de “y” en la primera ecuación, sustraes 2 “x” en ambos lados de la ecuación, reduces términos semejantes y obtienes 5 “y” igual a 145 menos 2 “x”.

Posteriormente divides ambos miembros de la igualdad entre 5, con lo que al simplificar obtienes “y” igual a 145 menos 2 “x”, entre 5.

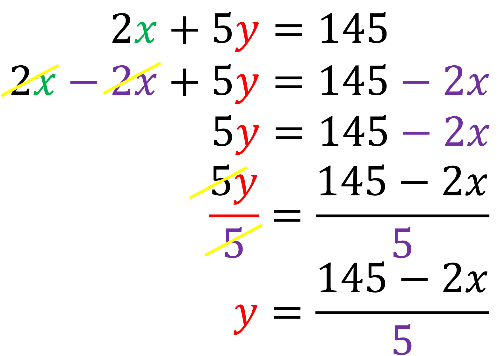
Con esto ya está despejada la “y” en la primera ecuación. Ahora, despejas la misma incógnita en la segunda ecuación.

En la ecuación 6 “x” más “y” igual a 113, sustraes 6 “x” en ambos lados de la igualdad, con lo que, al reducir términos semejantes, resulta “y” igual a 113 menos 6 “x”.

Y con ello ya queda despejada la incógnita en la segunda ecuación.

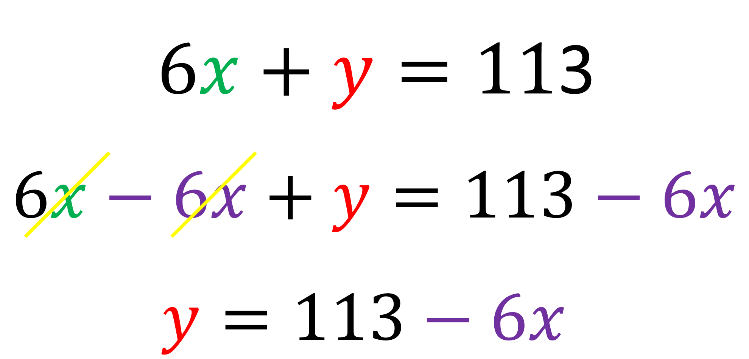
Observa los pasos que ahorras al elegir despejar una incógnita que visiblemente está “sola” o cuyo coeficiente es uno.

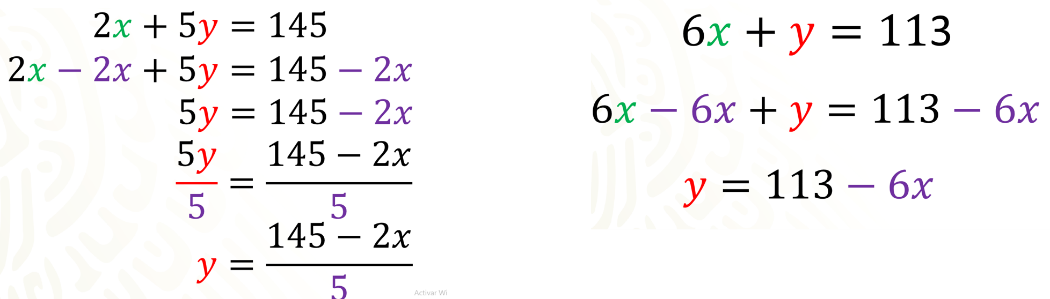
Ya que tienes la misma incógnita despejada en ambas ecuaciones, igualas estos despejes, obteniendo así la ecuación:

145 menos 2 “x”, entre 5 es igual a 113 menos 6 “x”.

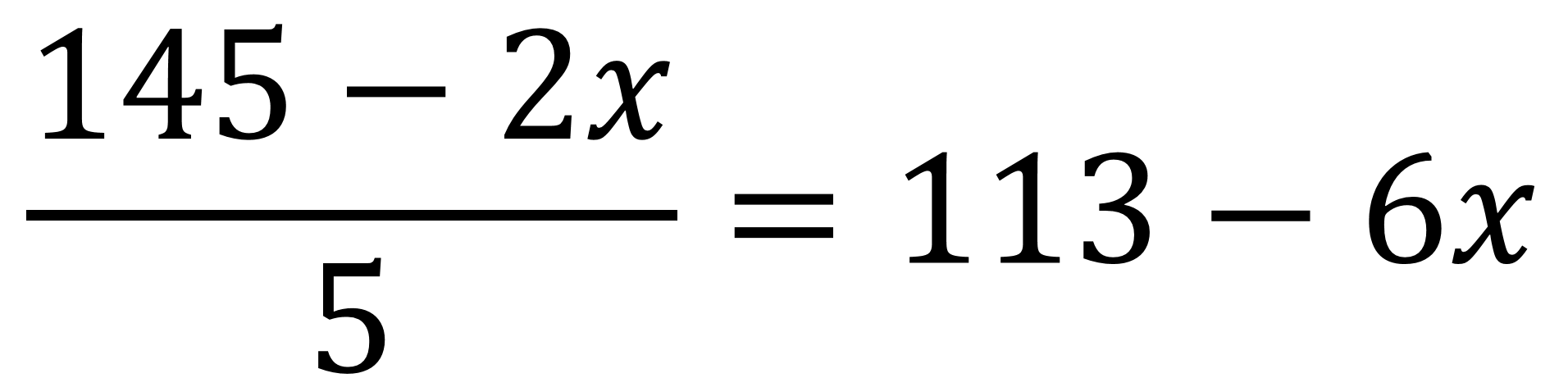
Nuevamente pasas de un sistema de dos por dos a un sistema de uno por uno.

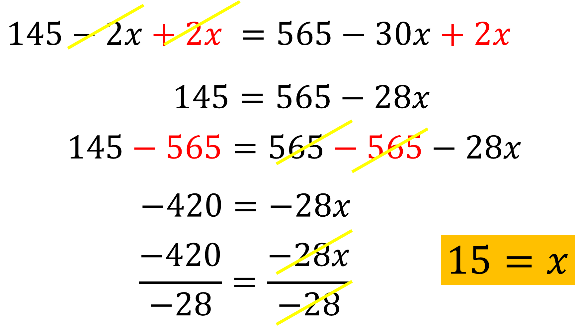
Para poder simplificar el 5 que está en el denominador del primer miembro de la ecuación, multiplica ambos miembros por 5.

Con ello obtienes la ecuación 5 por, abre paréntesis, 145 menos 2 “x”, entre 5, cierra paréntesis, igual a, abre paréntesis, 113 menos 6 “x”, cierra paréntesis, por 5.

Entonces se obtiene en el numerador de la primera fracción una multiplicación donde uno de ellos es 5 y, al tener un 5 en el denominador, puedes simplificarlo.

Ahora, multiplicas los factores del segundo miembro de la ecuación, 113 menos 6 “x” por 5.

Como 113 por 5 son 565, menos, 6 “x” por cinco son 30 “x”, la ecuación que se tiene es 145 menos 2 “x” igual a 565 menos 30 “x”.

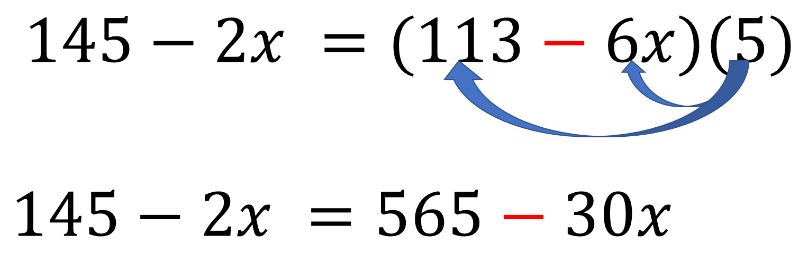
Adicionas 2 “x” en ambos lados de la igualdad, y al reducir términos semejantes tienes:

145 igual a 565 menos 28 “x”.

Ahora, sustraes 565 en ambos lados de la igualdad y obtienes 420 negativo igual a 28 “x” negativo.

Divide ambos lados de la igualdad entre 28 negativo. Con lo cual obtienes que 15 es el valor de “x”.

Una vez que determinas el valor de “x”, puedes sustituirlo en cualquier despeje de “y”. Recuerda que estos son:

“y” igual a 145 menos 2 “x”, entre 5, y “y” igual a 113 menos 6 “x”.

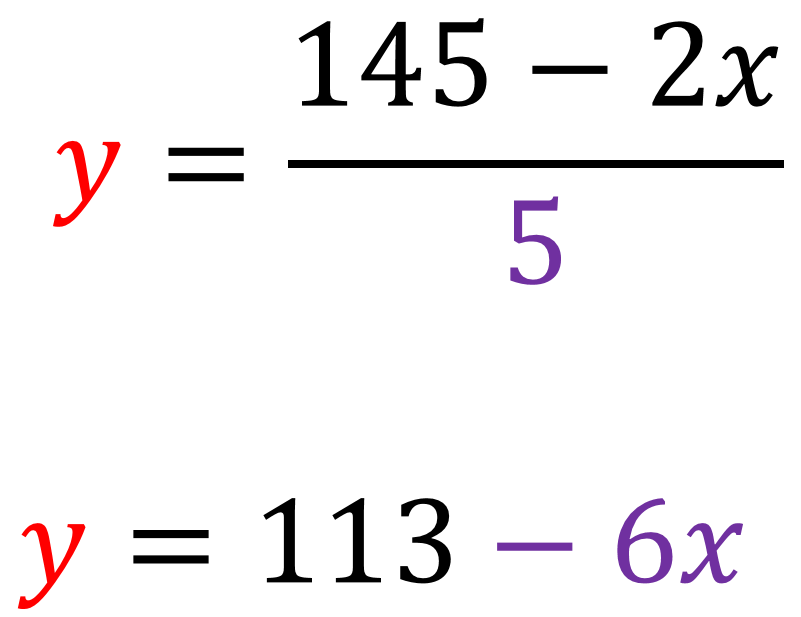
¿En qué despeje conviene sustituir el valor encontrado?

Conviene sustituir en el segundo despeje, ya que con ese realizarás menos operaciones.

Sustituirás ambos para que observes que obtendrás el mismo valor y que la cantidad de operaciones será menor si eliges el segundo despeje.

En el primer despeje tienes “y” igual a 145 menos 2 “x”, entre 5 y en el segundo, “y” igual a 113 menos 6 “x”.

Al sustituir el valor de “x” tienes, para el primer despeje, “y” igual a 145 menos, 2 por 15, entre 5 y en la segunda ecuación “y” igual a 113 menos 6 por 15.

Al resolver la multiplicación en ambos despejes tienes “y” igual a 145 menos 30, entre 5 para el primer despeje y “y” igual a 113 menos 90 en el segundo despeje.

Para el primer despeje debes calcular la diferencia de 145 menos 30, que resulta 115.

Ahora, al calcular el cociente de 115 entre 5, obtienes que “y” es igual a 23, mientras que, para el segundo despeje, al calcular la diferencia de 113 menos 90 obtienes que también aquí “y” es igual a 23.

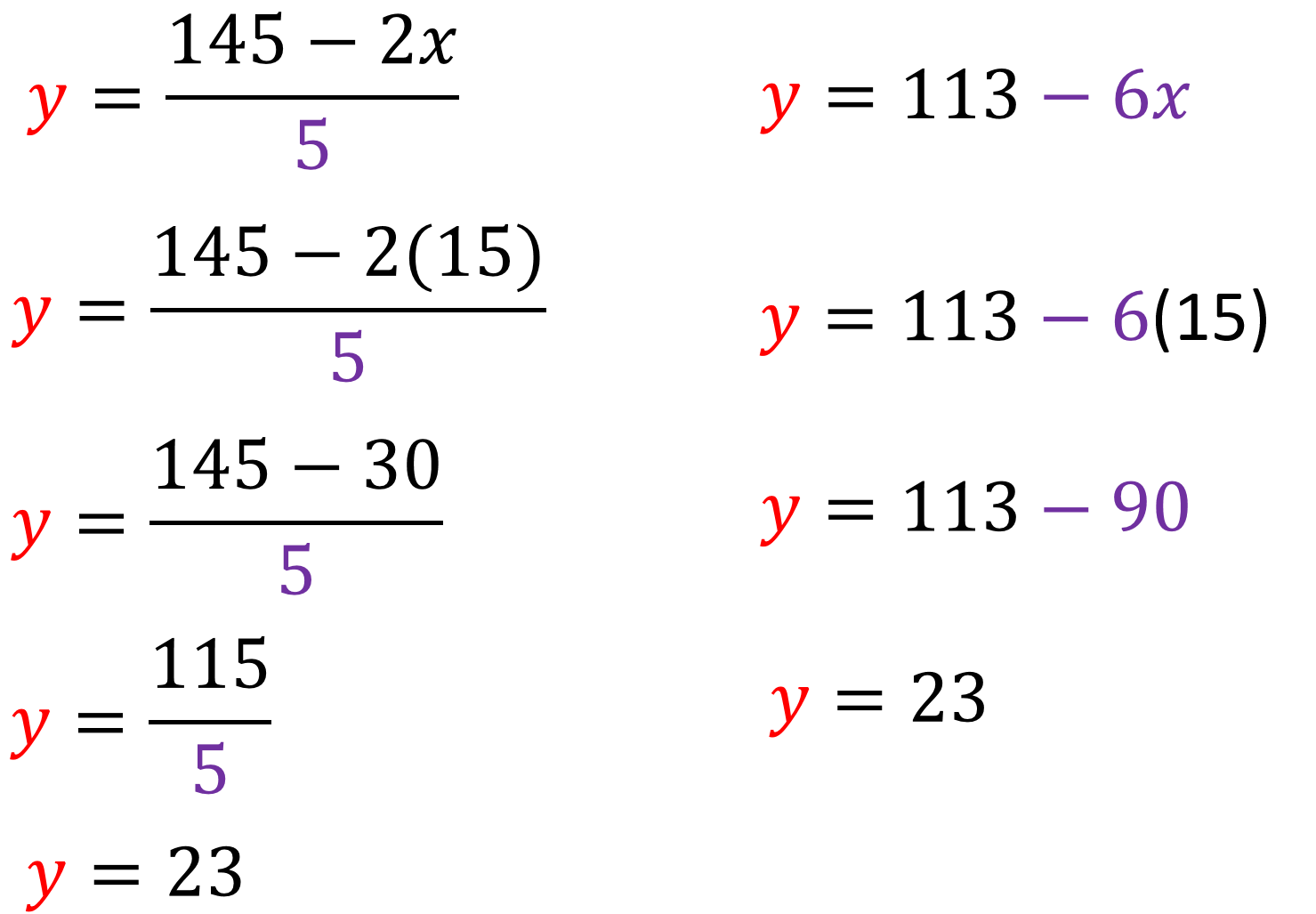
Observa que “y” es igual a 23 en ambos casos.

El reto de hoy:

En esta sesión has resuelto sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de sustitución. Recuerda que este es un material de apoyo y que, para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

¡Buen trabajo!

Gracias por tu esfuerzo.