¿Qué significa resolver una ecuación lineal?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42
¿Qué significa resolver una ecuación lineal?
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: representar y resolver situaciones con ecuaciones lineales.
¿Qué vamos a aprender?
En esta lección, se representarán situaciones problemáticas, a través de la modelación matemática, denominada ecuación lineal, de la forma ax + b = 0 y ax + b = cx + d; las cuales, se resolverán con la propiedad uniforme, pero se hará énfasis en la aplicación de las operaciones inversas. Asimismo, se dará significado a la solución de la ecuación formada y se analizará cómo dicha solución da respuesta a la situación que se modeló.
¿Qué hacemos?
Las ecuaciones son necesarias para resolver diversos planteamientos en los que se busca el valor de una incógnita que hace verdadera la igualdad, permiten relacionar diferentes variables y con ello explicar matemáticamente los fenómenos que se estudian. Es decir, siempre que está involucrada una incógnita y el signo de igual, se está en presencia de una ecuación, la cual, como ya sabes, consta de dos miembros separados por un signo de igual (=).
A propósito del signo de igualdad, sabías que su inventor fue el Matemático, Robert Recordé; que, en el año de 1557, se dio cuenta que era necesario representar con un símbolo a la igualdad y para no escribir la frase “es igual” durante un proceso operativo, decidió utilizar dos pequeñas líneas, del mismo tamaño y paralelas de manera horizontal.
Regresando al tema, se puede decir, que toda situación problemática de la vida cotidiana o científica, para su estudio, puede dar pie a una modelación matemática.
Ahora, se iniciará con la ecuación de primer grado, o lineal, usando el siguiente ejemplo:
Equis empresa otorga, una vez al año, una compensación económica extra a sus empleados; Enrique y María trabajan ahí. y recibieron una gratificación en su trabajo al final del año.
A Enrique le entregaron 6 vales y $1,000.00 y María recibió 4 vales y $5,000.00. Si los vales son de la misma denominación y los dos recibieron igual pago ¿a cuánto asciende la cantidad de cada vale?
Para resolver este problema matemático, se comenzará identificando las constantes y las incógnitas, esto es, los valores conocidos y desconocidos, respectivamente.
En este caso, puedes observar que hay dos cantidades de las cuales se conoce su valor, 1,000 pesos que le dieron a Enrique y 5,000 pesos que le dieron a María, por lo tanto, estas cantidades monetarias representan a las constantes.
Ambos recibieron dinero en vales, pero no se sabe, cuál es el valor de cada vale; por lo tanto, esta cantidad es la incógnita, la cual, se representa con la literal x.
Como a Enrique le dieron 6 vales, y de acuerdo a lo estudiado, esos seis vales se pueden representar algebraicamente como “6x”; del mismo modo, se pueden representar los cuatro vales que recibió María, como “4x”.
Por otro lado, ambos reciben el mismo pago, por lo que se establece una igualdad entre lo percibido por ambos; es decir, como a Enrique le entregaron 6 vales y 1000 pesos, se puede representar algebraicamente como: 6x + 1000, y María que recibió 4 vales y 5000 pesos, algebraicamente se representa como: 4x + 5000, formulando así la siguiente ecuación:
6x + 1000 = 4x + 5000
| Enrique | María | |
| 6 vales y $ 1 000 | 4 vales y $ 5 000 | |
| 6x + 1000 | 4x + 5000 |
Así, se ha representado la situación anterior mediante una ecuación lineal, de la forma:
ax+b=cx+d
Ahora, se resolverá la ecuación para determinar el valor de la incógnita.
Como se mencionó anteriormente, resolver una ecuación es encontrar el valor numérico de la incógnita de tal manera que al sustituirla en la misma ecuación se mantenga la igualdad.
Así que, para resolver una ecuación se puede despejar la incógnita utilizando las propiedades de igualdad. Pero ¿qué significa despejar una incógnita?
Una ecuación algebraica se compone de dos miembros, por lo que, despejar a una incógnita en una ecuación implica aislar o separar dicha incógnita, en cualquier lado de la igualdad.
Para este problema que se está revisando, se elige despejar el primer miembro de la igualdad, así que se emplearán las propiedades de la igualdad, principalmente la propiedad uniforme; pero retomando la pregunta: ¿qué significa despejar una incógnita?
Significa que se transferirá al segundo miembro los términos que no involucren a la incógnita, utilizando las operaciones inversas o contrarias.
¿Recuerdas qué es una operación inversa?
Una operación inversa es un proceso aritmético que implica realizar lo contrario de una operación aritmética, por ejemplo:
Lo inverso de la adición es la sustracción y lo inverso de la sustracción es la adición; asimismo, de la multiplicación, la división; y de la división, la multiplicación.
| Inversa de la… | ||
| Adición | Sustracción | |
| Sustracción | Adición | |
| Multiplicación | División | |
| División | Multiplicación | |
Como puedes observar en el problema que se está revisando, en ambos miembros de la igualdad se tiene una incógnita, con sus términos constantes.
Los números que afectan a la incógnita “x” son las constantes 1,000 y 5,000, así como sus coeficientes: 6 y 4, dando lugar a la ecuación:
6x + 1000 = 4x + 5000
En esta ecuación se hará uso de la propiedad uniforme de la igualdad que has estudiado anteriormente. Para ello, agruparás los términos con incógnita en el primer miembro y los términos constantes en el segundo miembro, aplicando las operaciones inversas; en este caso 4x, que está sumando en el segundo miembro, pasa restando al primer miembro, y por lo que respecta a la constante mil, la cual está sumando, se pasará al segundo miembro restando, quedando así:

Y en la ecuación, quedaría representado así:
6x - 4x = 5000 - 1000
Simplificando los términos semejantes, 6x menos 4x, te queda 2x, y a 5000 le restas 1000 obteniendo 4000:
2x = 4000
Para despejar la incógnita, pasas a su coeficiente 2, que la está multiplicando, al segundo miembro con su operación inversa, esto es, dividiendo al 4000.
Realizando la operación obtienes que “x” es igual a 2000.
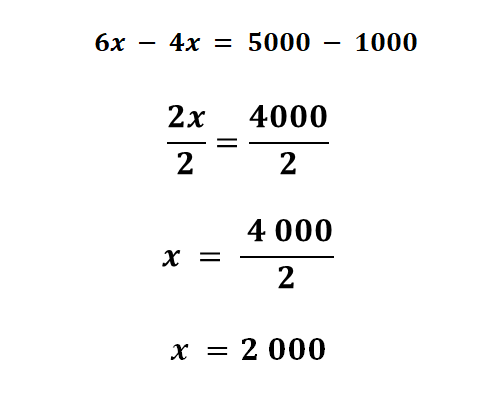
Esto significa que, el valor de cada uno de los vales es de 2,000 pesos, respondiendo así la pregunta del problema planteado.
Pero, ¿cómo sabes si el resultado es correcto?
Para comprobar que este resultado es el correcto, sustituyes el valor numérico obtenido en la ecuación que surgió a partir de la situación planteada, sustituyendo este valor en el lugar donde se encuentre la literal “x”. Como lo verás a continuación:
Retomando la ecuación original:
6x + 1000 = 4x + 5000
Vas a sustituir la incógnita “x”, escribiendo el valor numérico 2,000 en su lugar.
Cuando se tiene un número y una literal juntos, sin algún signo de suma o resta entre ellos, estos se están multiplicando; por lo tanto, como en la ecuación se tiene un término 6x esto significa que se multiplica 6 por 2000 y el otro término 4x es 4 por 2000, quedando como:
6(2000)+1000=4(2000)+5000
Realizando las operaciones correspondientes en ambos miembros de la igualdad, se obtiene que; 6 por 2000 es 12000 y 4 por 2000 es 8000.
Obteniendo así:
12000+1000=8000+5000
Al realizar la suma, en cada uno de los miembros, se obtiene que:
13000 = 13000
Por lo que la igualdad se mantiene, demostrando así que el valor obtenido de los vales al resolver la ecuación es el correcto; y que María y Enrique, recibieron el mismo pago.

Una ecuación, es una igualdad en donde hay una o varias incógnitas con un valor desconocido; para poder conocer dicho valor se resuelve la ecuación, aplicando las propiedades de la igualdad. Considera que se está explicando la manera común, esto es: “despejando la incógnita o valor desconocido, aplicando las operaciones inversas”.
Como has visto, las ecuaciones sirven para resolver algunas situaciones cotidianas, mediante su modelación matemática.
Revisa otro ejemplo, del uso y la solución adecuada, de una ecuación:
En ocasiones, en la época de cosecha ya sea de granos, vegetales o frutas, los comuneros de tierras ejidales juntan sus cosechas para venderlas a un solo distribuidor. Tal fue el caso de los comuneros Martín, Ricardo, y la comunera, Raquel; quienes juntaron sus cosechas para venderlas a una sola persona. La cosecha de Raquel corresponde al doble de la cosecha de Ricardo. La cosecha de Ricardo corresponde al triple de la cosecha de Martín. Si el distribuidor les pagó 63,000 pesos por todo, ¿cuánto dinero deben recibir Raquel, Ricardo y Martín en relación a su respectiva cosecha?
¿Cómo se puede determinar lo que debe recibir cada quién?
Una estrategia que se puede seguir es, modelar esta situación mediante una ecuación; para ello, considera, que debes identificar, las cantidades conocidas y desconocidas, es decir, las constantes y las incógnitas.
En esta situación puedes identificar rápidamente una constante. En este caso, la constante son los 63,000 pesos que recibieron por el pago de toda la cosecha que juntaron los tres. Pero, no se sabe exactamente la cantidad de cosecha que aportó cada quien; por lo tanto, esto corresponde a una incógnita, la cual se puede representar mediante la literal x.
Así, se puede representar lo que cosechó Martín como “x”. Como la cosecha de Ricardo corresponde al triple de la de Martín, se puede representar la cosecha de Ricardo como “3x”. Ahora, sólo queda representar la cosecha que aportó Raquel, la cual es el doble de la aportación de Ricardo, y como la de Ricardo se representó como “3x”, entonces se puede representar la cosecha de Raquel como “2 por 3x”, pero esta expresión algebraica indica un producto; por lo tanto, dicha expresión queda simplificada como “6x”

Con las expresiones algebraicas que se han obtenido, las cuales corresponden a tres personas, se puede formular una ecuación, tomando en cuenta que la cosecha que corresponde a Raquel más la de Ricardo más la de Martín es equivalente a 63,000 pesos, obteniendo así el modelo matemático, del cual se obtuvo una ecuación lineal que es:
6x + 3x + x = 63000
Por lo tanto, para determinar la cantidad de dinero que le corresponde a cada persona, hay que resolver esta ecuación.
Ya sabes que resolver una ecuación es encontrar el valor de la incógnita que mantenga la igualdad, para ello analiza qué debes hacer.
Observa que, las expresiones que están en el miembro izquierdo —6x, 3x y x— son términos semejantes, por lo que las puedes sumar obteniendo 10x, reduciendo la ecuación a: 10x=63000
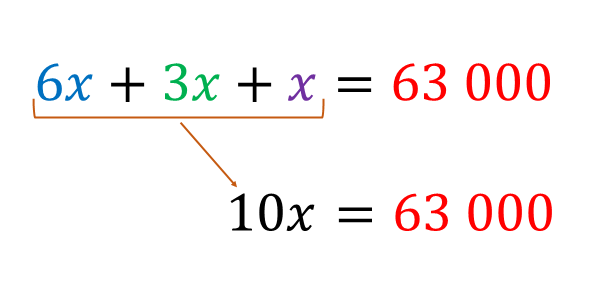
Para encontrar el valor de la incógnita que hace verdadera la igualdad, aplicarás las propiedades de la igualdad. Has aprendido que dichas propiedades permiten “despejar la incógnita”. En este caso, puedes aplicar la propiedad uniforme, del mismo modo que la estudiaste. Esta propiedad dice que, puedes sumar, restar, multiplicar o dividir la misma cantidad a ambos miembros de la igualdad, y la igualdad se conserva.
Entonces, ¿qué operación puedes hacer, en ambos miembros de la igualdad, para despejar la incógnita?
¿Sumar 10, restar 10, dividir entre 10 o multiplicar por 10?
La respuesta es que, ya que el coeficiente 10 está afectando a la incógnita “x”, entonces para despejarla, hay que dividir entre 10 a ambos miembros de la igualdad, obteniendo así 10x entre 10 y 63000 entre 10
Al dividir 10 entre 10, en el primer miembro, se obtiene 1, recuerda que el 1 se puede o no escribir.
Y, al calcular el cociente, en el segundo miembro, de 63000 entre 10, se obtiene el valor de la incógnita “x”, el cual es de 6300
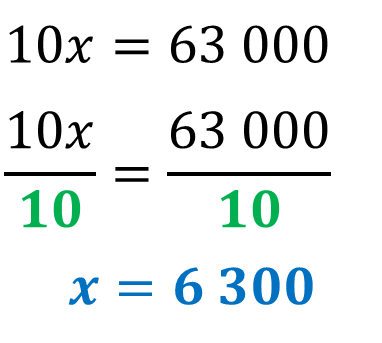
Has llegado a la solución de la ecuación, en donde el valor que corresponde a la incógnita x es 6300
Ahora, ¿de qué manera, esta solución, te ayuda a determinar la cantidad de dinero que debe recibir cada quien, de acuerdo a la cantidad de su cosecha?
Como la cosecha de Raquel se representó, algebraicamente, como “6x” y el valor de “x” que se encontró al resolver la ecuación es 6300, sólo sustituyes dicho valor en la expresión algebraica, de la siguiente manera: 6 por 6,300. Al resolver este producto, se obtiene 37,800
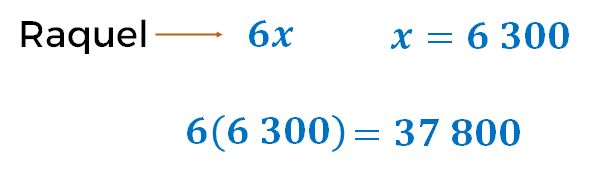
Esto significa que Raquel recibió 37,800 pesos, por su respectiva cosecha.
Del mismo modo, calcula lo que recibió Ricardo lo cual fue representado, algebraicamente, como “3x”, es decir, sustituye el valor numérico de x, 6300, en dicha expresión, de la siguiente manera: 3 por 6,300, se obtiene 18,900
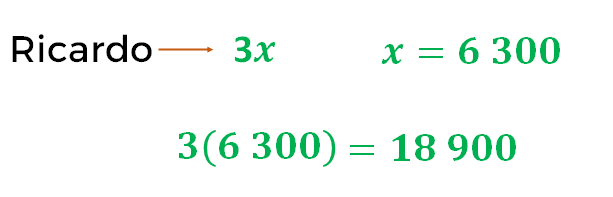
Entonces, Ricardo recibió 18,900 pesos por su respectiva cosecha.
Por último, la cosecha que corresponde a Martín se representó con la literal “x”, y como x es igual a 6,300, entonces, Martín recibió 6,300 pesos por su respectiva cosecha.
Bien, has determinado la cantidad de dinero que le corresponde a cada persona. Para verificar que lo que recibieron fue correcto, obtén el total de lo que recibieron respectivamente, ya que la suma de las tres cantidades tiene que ser igual a 63,000 pesos.
37,800 pesos que recibió Raquel más 18,900 de Ricardo más los 6,300 de Martín, se obtienen los 63,000 pesos que les pagó el distribuidor.
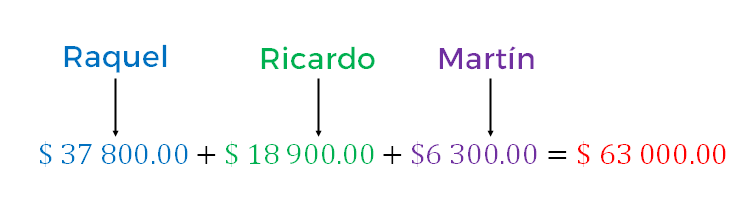
Observa que, al modelar algebraicamente esta situación, te permitió determinar una solución a una situación que está inmersa en un contexto cotidiano.
En tu libro de texto puedes buscar el aprendizaje esperado que estas estudiando; en él podrás encontrar la siguiente información:
Resolver una ecuación significa encontrar el valor de la incógnita para el cual el número representado en el miembro izquierdo del signo de igualdad es el mismo que el número del miembro derecho.
Por ejemplo;
En la ecuación 3x-1=20, la solución es x=7, ya que al sustituir este valor en la misma tenemos que 3(7)-1=20.
La solución de una ecuación lineal con una incógnita es un único número, es decir, no puede haber dos valores distintos de la incógnita que hagan cierta a la igualdad.
Por ejemplo, x=2, no es solución de 3x-1=20, ya que 3(2) -1 = 5, lo cual es diferente a 20.
Así es, una ecuación lineal puede tener sólo una solución o ninguna; y, además, esta solución resuelve una situación, que se puede presentar en tu vida diaria, mediante un modelo matemático llamado ecuación.
Revisa un ejemplo más para modelar algebraicamente una situación de tu contexto y encontrar su respectiva solución al resolver la ecuación que se forme de acuerdo a dicha problemática.
Para celebrar alguna festividad, se tiene por costumbre colocar adornos; por ejemplo, al celebrar el Día de Muertos, en el país, se adorna con papel picado; en los cumpleaños se colocan globos, serpentinas; entre otros. Para ello, es necesario comprar los adornos o hacerlos para economizar gastos. Así como lo hizo la señora Bernabé, quien realizó sus propios adornos para celebrar el cumpleaños de su hijo.
Para hacer sus adornos ha cortado rectángulos de papel de 225 cm cuadrados de área para dividirlos en dos secciones y pintar de color naranja la parte de arriba y de color verde la de abajo. La siguiente figura representa un modelo de dicho adorno. ¿Cuánto mide el ancho de la sección de color naranja?
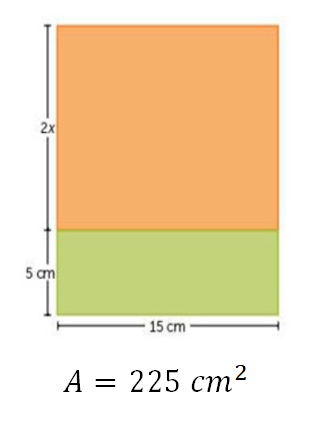
Para responder, construye una ecuación que modele esta situación.
Observa que se tiene la superficie total del rectángulo que se va a seccionar, la cual es de 225 centímetros cuadrados; este es un dato conocido, por lo que es una constante. Por otro lado, también se tiene otro dato, el cual es la longitud de uno de sus lados, siendo éste de 15 centímetros, por lo que se tiene otra constante.
Como uno de sus lados se secciona en dos partes que no son iguales, éste se compone de la suma de 5 cm, más 2x, siendo la sección de 2x el valor numérico que debes determinar; por lo tanto, es un dato desconocido y la incógnita en este caso es la literal “x”.
Recuerda que para calcular el área de un rectángulo basta con multiplicar su base por su altura.
Por lo tanto, para determinar el valor del ancho del rectángulo de color naranja, aplica la fórmula para calcular el área del rectángulo grande, la cual es A= b(h), con los datos que se te proporcionan, esto es, si consideras que la base del rectángulo grande es el lado con la longitud de 15 cm, su altura, la suma de 5 cm más 2x y su área la cual también se te proporciona, es de 225 centímetros cuadrados, puedes modelar una ecuación sustituyendo estos datos en la fórmula del área del rectángulo, obteniendo así la siguiente ecuación:
225 es igual al producto de 15 por la suma de 5 más 2x
Aplicando la propiedad simétrica de la igualdad, en donde dice que se pueden cambiar el orden de los miembros sin que la igualdad se altere, cambia el orden de tu ecuación para que la incógnita quede del lado izquierdo de la igualdad y después despejar la incógnita, para que quede de la siguiente manera:
15 por la suma de 5 más 2x igual a 225

Para resolver la ecuación aplica la propiedad distributiva, multiplicando al factor 15 por cada uno de los términos del otro factor, obteniendo:
15 por 5, más 15 por 2x igual a 225
Donde al realizar las multiplicaciones, se obtiene:
75 + 30x = 225

Tal como se ha explicado en esta lección, para resolver la ecuación, hay que despejar la incógnita y para ello, utilizas la propiedad uniforme de la igualdad.
¿Qué operación se debe hacer para ello?
La respuesta es que, restas 75 en ambos miembros de la igualdad obteniendo:
75 - 75 + 30x = 225 - 75
Que al realizar las operaciones aritméticas se obtiene:
30x = 150
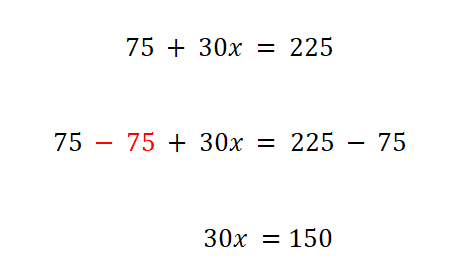
Sabes que despejar la incógnita es dejarla sola. ¿Qué te falta por realizar?
Así es, quitar su coeficiente 30, por lo que divides entre 30 a ambos miembros de la igualdad, esto es: 30x entre 30 igual a 150 entre 30, por lo que, al dividir 30 entre 30 se queda únicamente la “x”, y al dividir 150 entre 30 se tiene un resultado de 5, obteniendo así el valor de la incógnita, por lo que “x” es igual a 5.
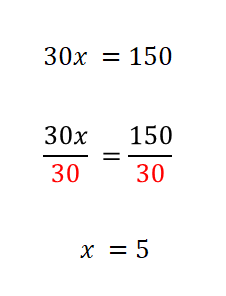
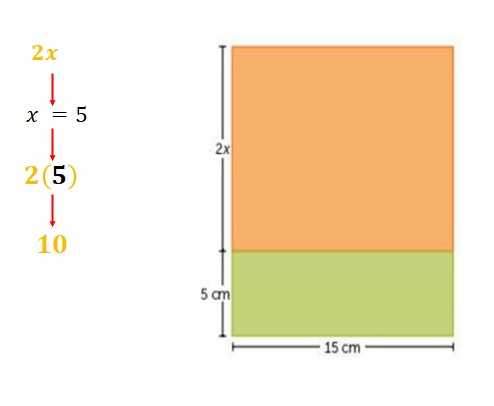
Por lo tanto, al retomar el lado representado con “2x”, en el rectángulo de color naranja que se quiere determinar. Únicamente sustituyes el valor obtenido en la expresión “2x”, quedando como 2 por 5, y al realizar la multiplicación se obtiene la medida del ancho del rectángulo de color naranja, siendo éste de 10 cm. Así, se da respuesta a la pregunta: ¿Cuánto mide el ancho de la sección de color naranja?
Haciendo un recuento de lo que revisaste este día, se puede decir que en esta lección se resolvieron situaciones de tu entorno traduciéndolas al lenguaje algebraico, dando lugar a ecuaciones de las formas ax+b=c y ax+b= cx+d, a las que se les conoce como ecuaciones lineales o de primer grado.
También se estudió que, para comprobar los resultados, se sustituye el valor obtenido de la incógnita en la ecuación original y se comprueba que si cumple la igualdad el resultado al resolver la ecuación entonces es correcto, y si no se cumple la igualdad el resultado es incorrecto.
Has concluido el tema del día de hoy. Si quieres conocer más sobre este tema, revisa tu libro de texto y resuelve situaciones similares a las que se plantearon en esta sesión. Asimismo, si tienes alguna duda acércate con tu profesor o profesora de esta asignatura.
El reto de hoy:
Comprueba que el valor numérico de la incógnita del último ejercicio que realizaste en esta sesión, relacionado con los adornos de fiesta, sea el correcto. Para ello debes realizar la sustitución del valor de la incógnita x = 5 en la ecuación original y resolver las operaciones aritméticas correspondientes, de tal manera que se cumpla la igualdad.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion