Euclides: la organización de la geometría

Euclides: la organización de la geometría

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: reconocer las aportaciones de Euclides a las matemáticas.

¿Qué vamos a aprender?

En esta sesión, conocerás sobre las aportaciones de uno de los matemáticos más importantes de la historia, Euclides, quien realizó contribuciones significativas en la organización de la geometría.

¿Qué hacemos?

Para comenzar a entender la organización de la geometría, analiza lo siguiente.

Para medir el largo y ancho de un salón basta con colocar directamente un metro sobre la superficie de la pared y realizar la medición correspondiente. Sin embargo, medir directamente no es algo que se pueda hacer siempre en todos los contextos. Por ejemplo, si se quiere medir la altura de un edificio sería muy difícil realizarlo de esta manera. Entonces, ¿cómo se realizaría esta medición?

Para resolver problemas de distancias inaccesibles, en lugar de realizar directamente las mediciones sobre los objetos reales, se elaboran representaciones en papel y se trabaja con ellas. Pero ¿cómo se puede verificar que la medición sea correcta?, ¿cómo se pueden realizar afirmaciones con seguridad sobre un objeto real, utilizando únicamente la representación en papel?

Para asegurar que las afirmaciones sobre los modelos en papel sean correctas, se tiene que razonar de manera distinta a como se hace en mediciones directas con objetos reales. Este tipo de razonamiento es una contribución de Euclides a las matemáticas.

Con la organización de la geometría, se han podido resolver problemas como medir la altura de una pirámide o calcular la distancia de un barco a la costa sin tener que utilizar un metro o algún instrumento para realizar la medición directamente. Entonces, para obtener conclusiones verdaderas sobre el mundo físico sin tener que manipular objetos reales, se toman como punto de partida algunas afirmaciones que se consideran verdaderas. Pero ¿cuáles son esas verdades?

Las verdades inmediatas o evidentes aplicables para todas las ciencias, se pueden llamar nociones comunes o axiomas; y las verdades inmediatas específicas para la geometría, se pueden llamar postulados. De esta manera, una afirmación es que, es posible trazar una línea recta desde cualquier punto a cualquier otro.

Para comprender la afirmación: “es posible trazar una línea recta desde cualquier punto a cualquier otro”, es necesario definir qué es un punto y qué es una recta. Analiza las siguientes definiciones que te servirán como punto de partida.

1. Un punto, es lo que no tiene partes, es decir que sólo tiene posición.
   
2. Una línea es una longitud, sin anchura.
   
3. Los extremos de una línea son puntos.
   
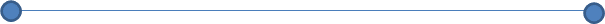
4. Una línea recta es aquella que yace por igual respecto de los puntos que están en ella.
   
5. Una superficie es lo que sólo tiene longitud y anchura.
6. Los extremos de una superficie son líneas.
7. Una superficie plana es aquella que yace por igual respecto de las líneas que están en ella.
   
8. Un círculo es una figura plana rodeada por una línea tal que todas las rectas que inciden sobre ella desde cierto punto interior a la figura son iguales entre sí.
9. El punto interior se llama centro del círculo.
10. Un diámetro del círculo es una recta cualquiera trazada que pasa por el centro y limitada en ambos sentidos por la circunferencia del círculo, recta que también divide el círculo en dos partes iguales.

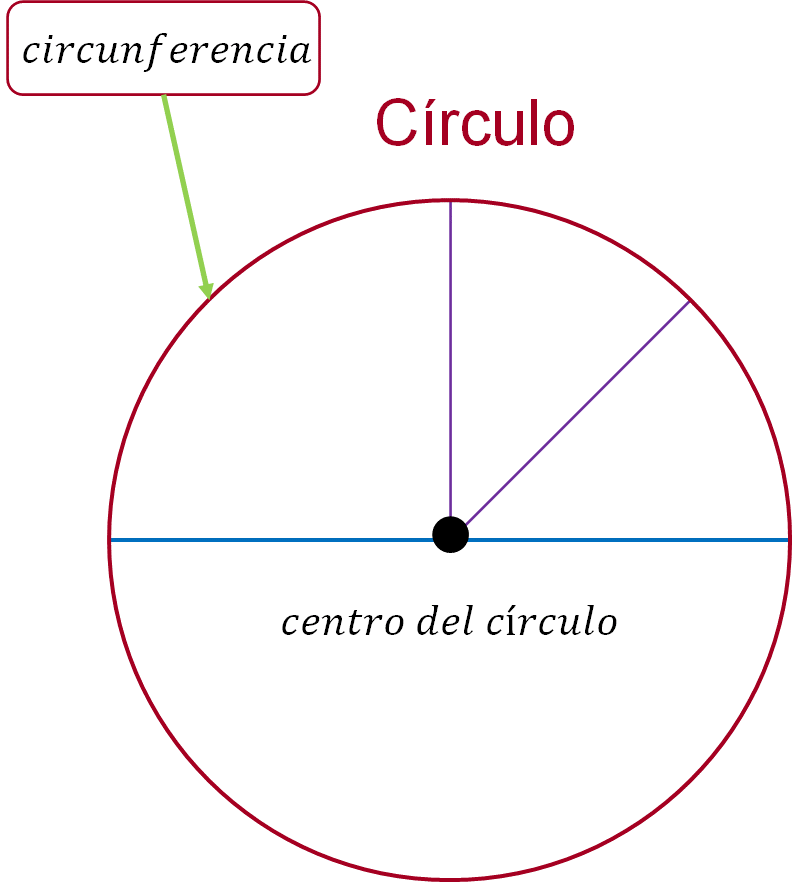
A muchos matemáticos, estas definiciones les parecen oscuras o poco claras. Se cree que algunas de estas definiciones fueron inspiradas por objetos del mundo real. Por ejemplo, la definición de línea recta parece que fue inspirada por el nivel que se usa en albañilería o el borde de una regla.

Ahora, continúa con las afirmaciones que se consideran inmediatamente verdaderas. Comienza por aquellas para todas las ciencias, es decir, las nociones comunes o axiomas.

Noción uno: las cosas que sean iguales a una misma cosa son también iguales entre sí.

Noción dos: si a cosas iguales se agregan cosas iguales, los totales son iguales.

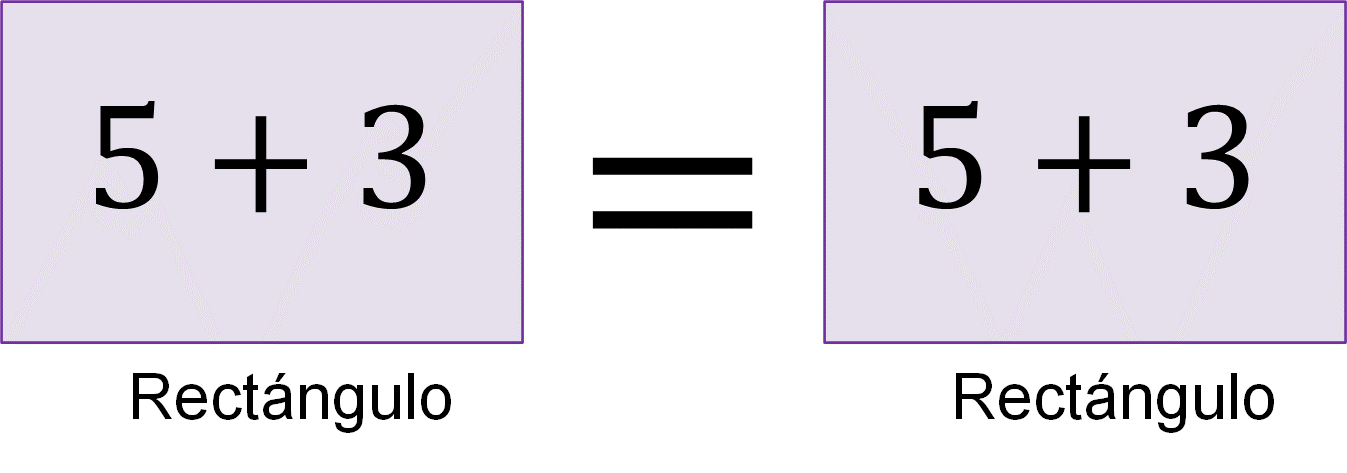
Noción tres: si de cosas iguales se quitan cosas iguales, los restos son iguales.

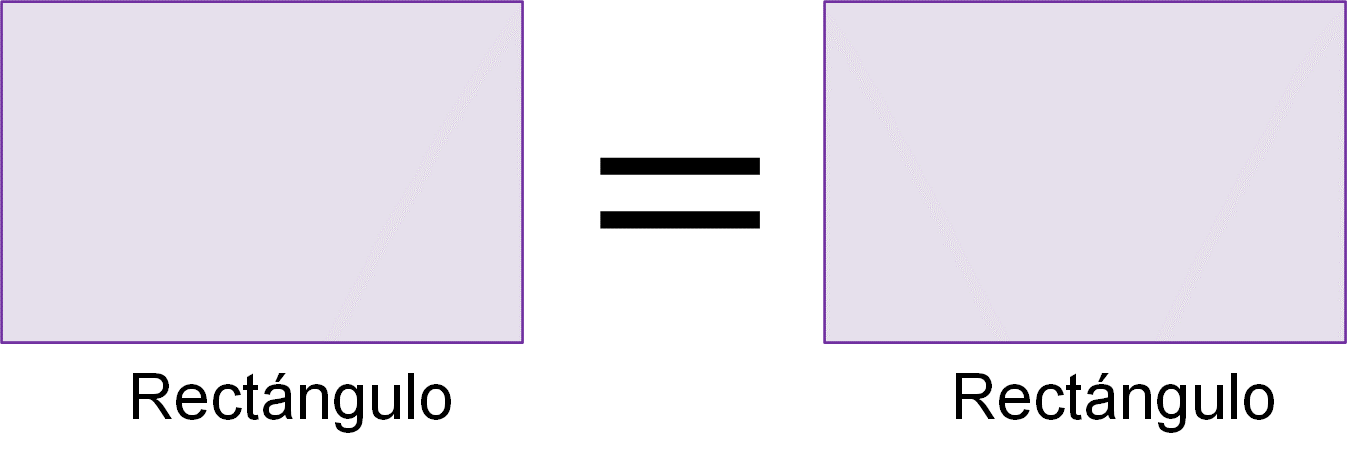
La segunda y tercera noción se refieren a la legitimidad de sumar y restar cosas iguales. La última introduce la desigualdad.

Noción cuatro: las cosas que se superponen una a la otra son iguales entre sí, por lo tanto, si una figura se puede trasladar sobre el plano de modo que, al colocarse sobre otra, ambas figuras coinciden perfectamente; se superponen y entonces las dos figuras son iguales en todos sus aspectos, es decir, tienen los mismos ángulos, los mismos lados y demás elementos.

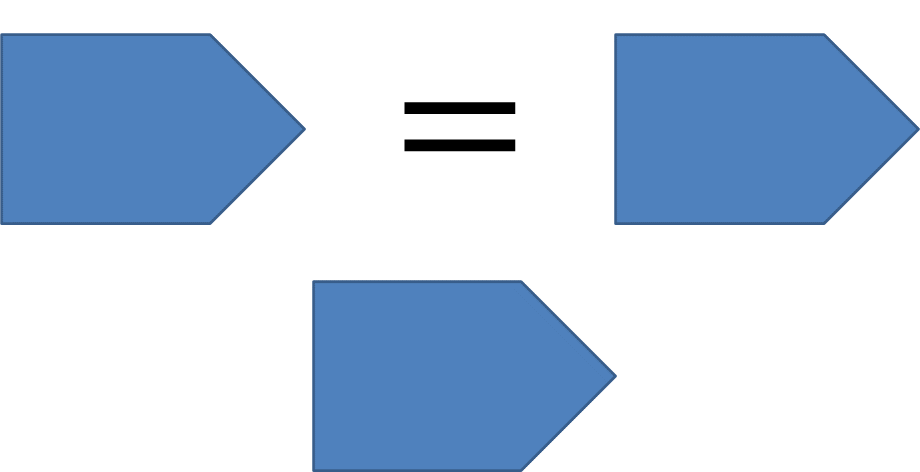
Noción cinco: el todo es mayor que la parte.

Estas afirmaciones son verdaderas, por lo que se considera que no se requiere ninguna explicación. Ahora continúa con las verdades inmediatas específicas para la geometría. Lo que se conoce como postulados:

1. Es posible trazar una línea recta desde cualquier punto a cualquier otro.
2. Es posible prolongar continuamente en línea recta, una recta dada.
   
   ¿Estás de acuerdo en que esas afirmaciones son verdaderas? ¿Necesitas alguna explicación adicional? Analiza la siguiente:
3. Es posible trazar un círculo con cualquier centro y radio.

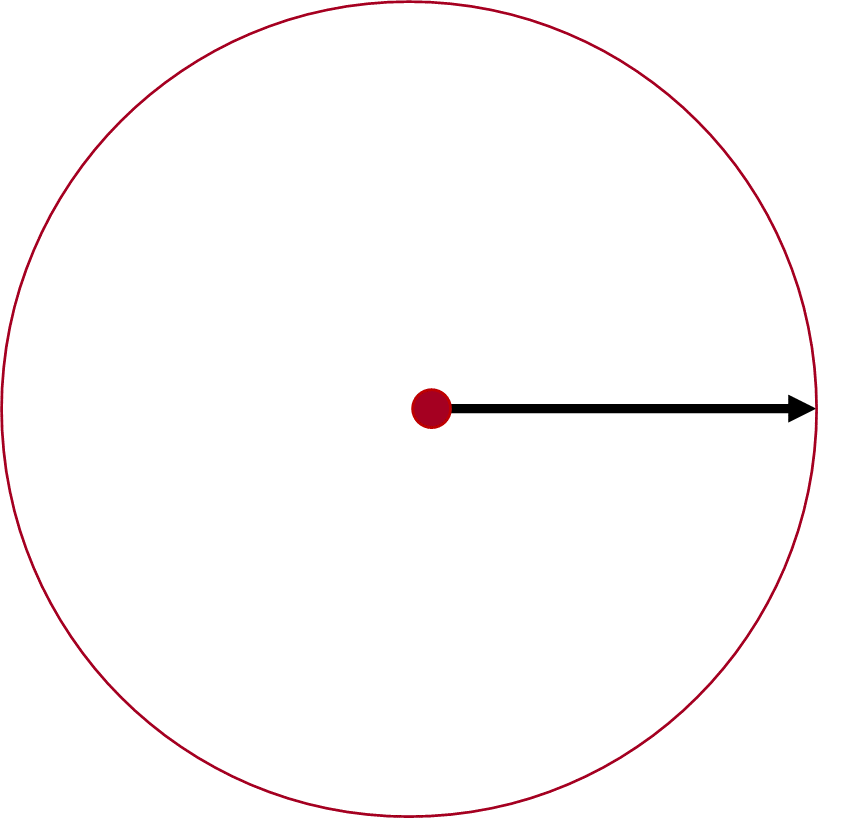
A los griegos, estas afirmaciones les parecían verdaderas inmediatamente, sin ninguna explicación. Les parecía evidente el hecho de que es posible trazar una línea recta desde cualquier punto a cualquier otro; que es posible prolongar continuamente en línea recta, una recta dada; o que es posible trazar un círculo con cualquier centro y radio. Quizá conozcas algunas de estas afirmaciones. En este grado, por ejemplo, has visto la definición del círculo y también se ha hecho referencia a las propiedades de la igualdad para, por ejemplo, resolver ecuaciones.

A partir de estas verdades, se pueden obtener afirmaciones que con seguridad corresponden con el mundo físico. Por ejemplo, imagina que quieres representar en papel un objeto físico con forma de triángulo equilátero, es decir, un triángulo cuyos lados miden lo mismo, ¿cómo lo construirías?

Se podría construir con una regla graduada, pero ¿y si sólo cuentas con una regla sin marcas y un compás que al levantarlo del papel se cierra inmediatamente?, ¿cómo lo harías? Piensa un momento, antes de que se dé la solución.

Se pueden utilizar las definiciones y afirmaciones evidentes que se han visto hasta ahora. Inicia con una recta AB, este podría ser un lado del triángulo.

¿Cómo se podrían construir los otros dos lados del triángulo? Recuerda que esos lados deben tener igual medida que AB.

Para entenderlo mejor, reflexiona en lo siguiente: ¿cómo se puede trazar una recta con igual medida que la de la recta AB? No olvides que sólo se cuenta con una regla sin graduar y un compás. También se cuenta con las definiciones, axiomas y postulados que has visto.

Retoma la definición del círculo: en un círculo todas las rectas que se trazan desde su centro a la circunferencia tienen igual medida. Si, además, se sigue un postulado descrito anteriormente, se puede trazar un círculo con cualquier centro y radio.

Específicamente, como se necesita una recta de igual tamaño que AB, se puede construir un círculo con centro A y radio AB. Se llamará a este círculo BCD.

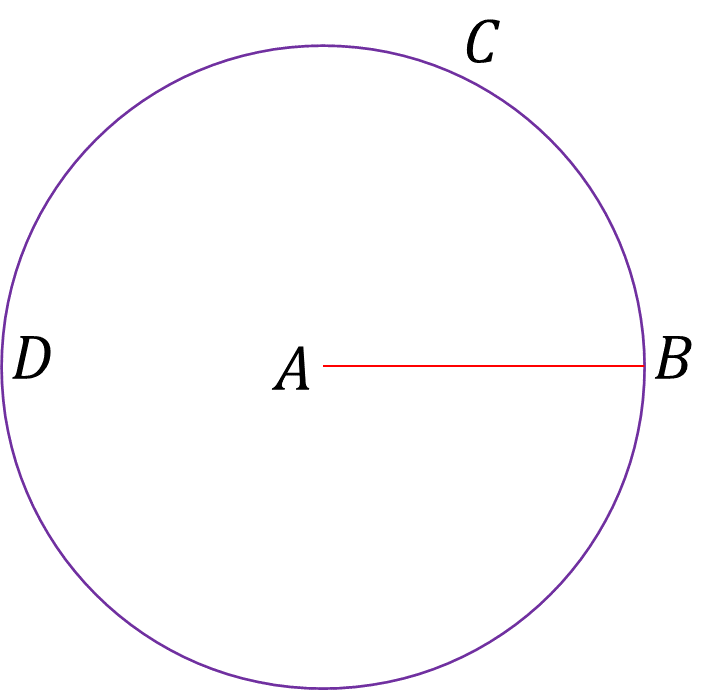
Así, todos los radios de ese círculo tendrán igual medida que AB. Ahora, se pueden trazar esos radios porque un postulado lo permite: es posible trazar una línea recta desde cualquier punto a cualquier otro. En particular, es posible trazar el radio desde el punto C al punto A.

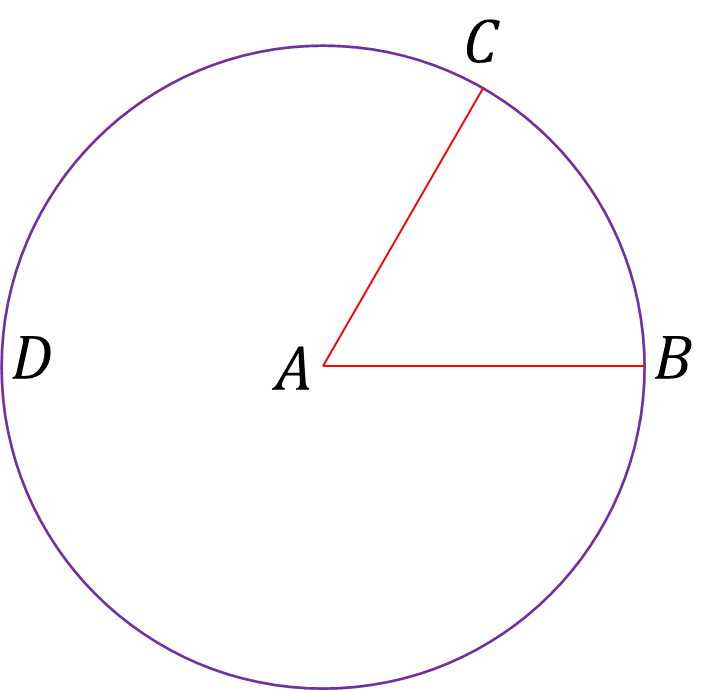
De este modo, se ha obtenido la línea recta CA de igual tamaño que AB utilizando sólo regla sin graduar, el compás que se cierra y las definiciones y afirmaciones evidentes que se han visto anteriormente.

Para trazar otra recta que complete el triángulo y que sea del mismo tamaño que AB, se puede seguir un razonamiento similar. Es decir, con base en la definición del círculo y el postulado correspondiente pero ahora con centro en B y radio BA. A este círculo se le puede llamar AEC.

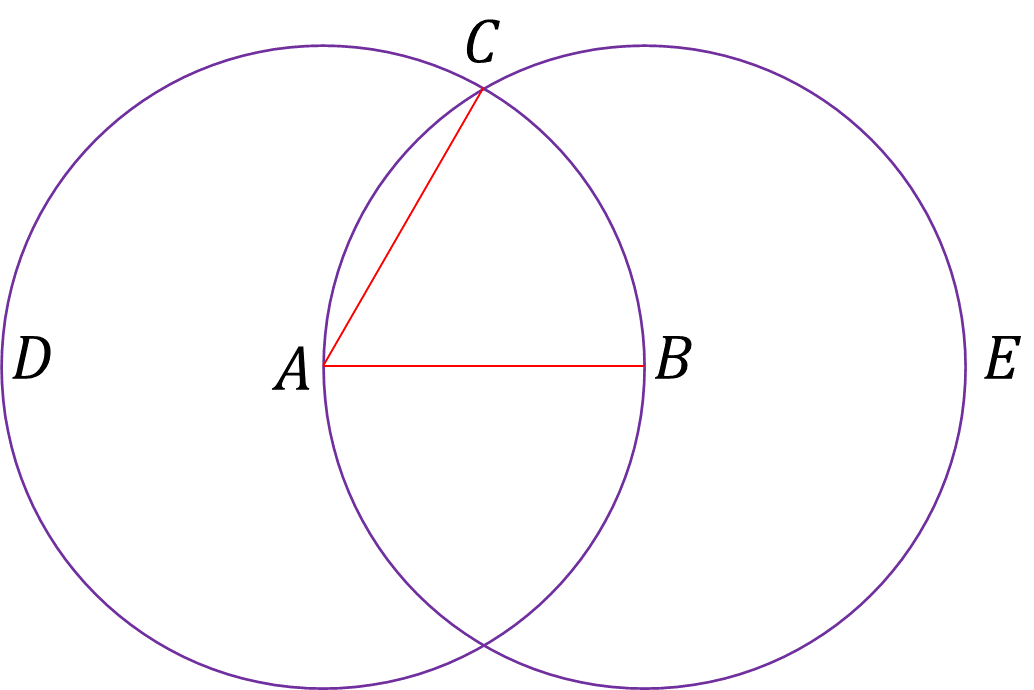
Con esto, todos los radios de este círculo tendrán igual medida que BA. Se pueden trazar esos radios porque un postulado lo permite: es posible trazar una línea recta desde cualquier punto a cualquier otro. En particular, es posible trazar el radio desde el punto C al punto B.

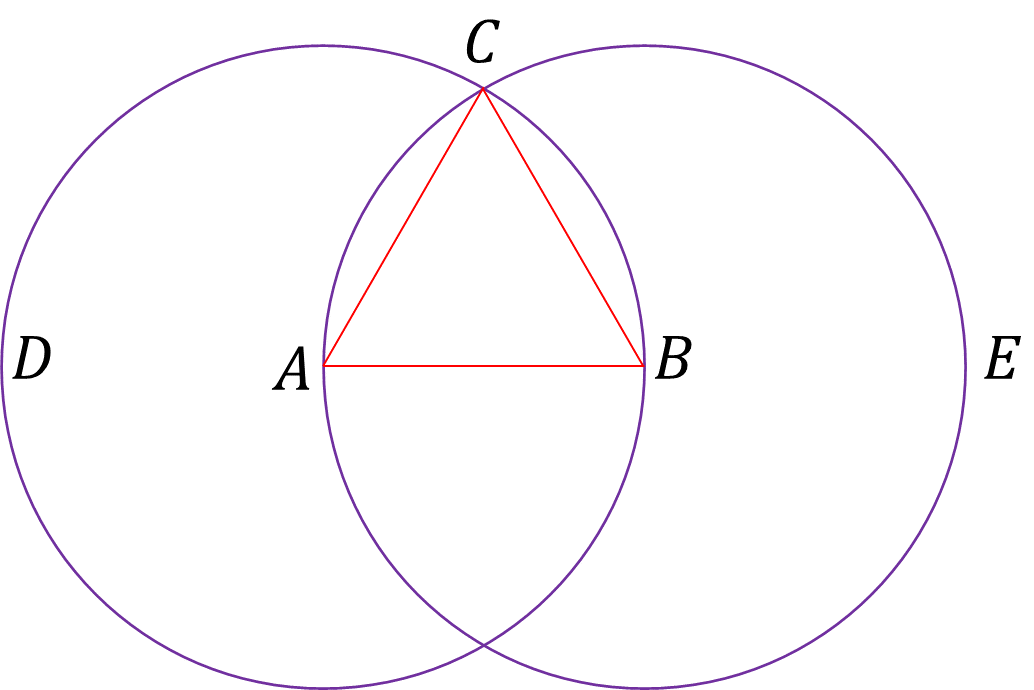
Se ha obtenido una línea recta CB de igual tamaño que BA utilizando sólo regla y compás, y las definiciones y afirmaciones evidentes que se han visto anteriormente.

Hasta aquí has formado un triángulo de tal manera que AB es igual, por un lado a CA, y por otro a CB. Pero ¿cómo podrías estar seguro, sin realizar medición alguna con regla graduada, de que CA es igual a CB?

Según una noción común o axioma que has visto anteriormente, las cosas iguales a una misma cosa son también iguales entre sí. Por lo tanto, como CA y CB son iguales a AB, entonces CA es también igual a CB; de este modo, las tres rectas CA, AB, CB son iguales entre sí. Así, se ha construido un triángulo equilátero.

Esta es una forma en la que se puede ir pensando la solución al problema de construir un triángulo equilátero contando sólo con una regla graduada y un compás que se cierra. Sin embargo, la forma de presentar la solución puede cambiar. Por ejemplo: “sea AB la recta finita dada”.

Considerando el postulado según el cual es posible trazar un círculo con cualquier centro y radio, se puede construir un círculo con centro A y radio AB, es decir, el círculo BCD.

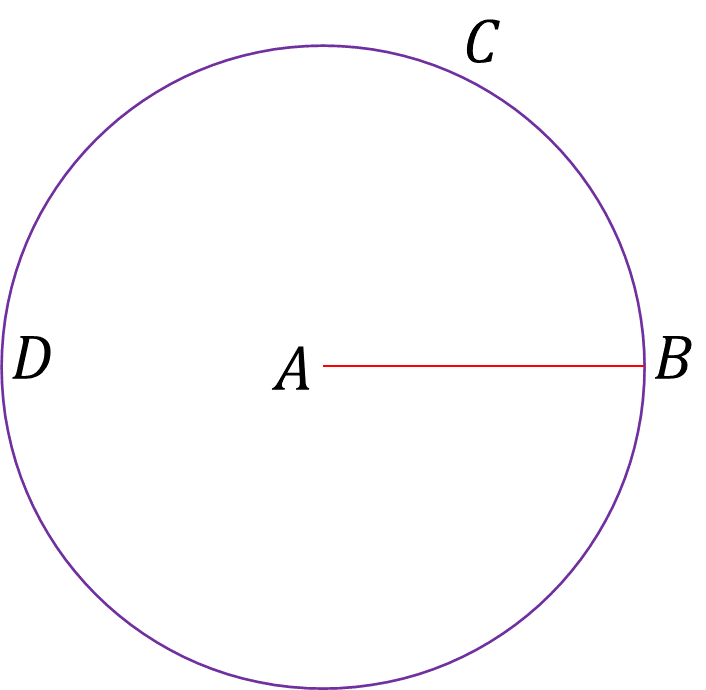
Y con el centro B y la distancia (radio) BA, se puede trazar a su vez el círculo ACE.

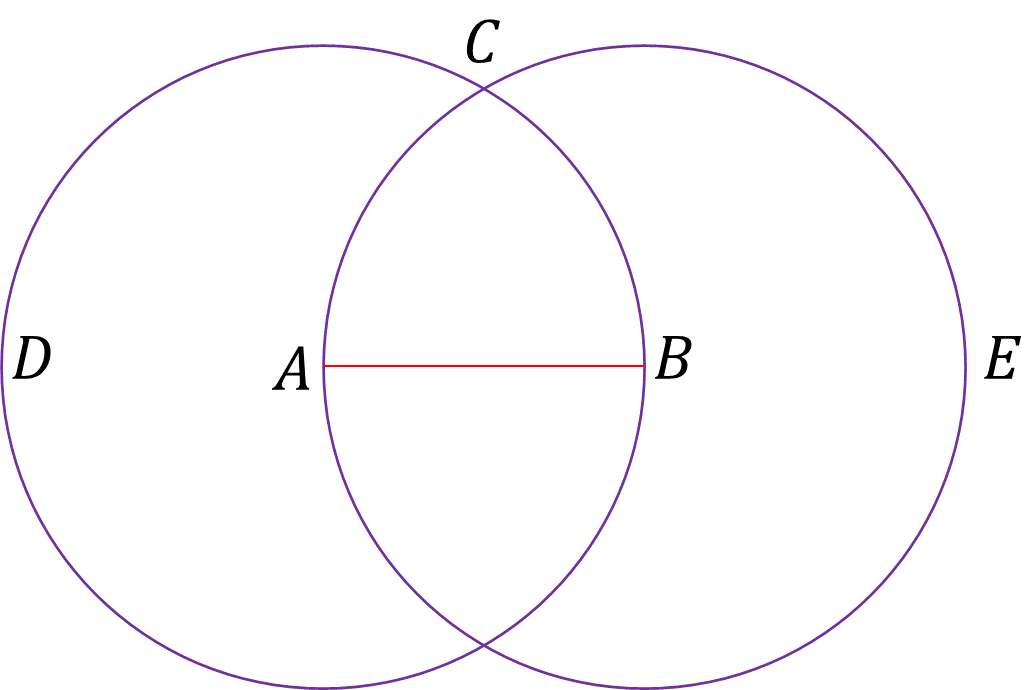
Y a partir del punto C donde los círculos se cortan entre sí, se trazan las rectas CA y CB hasta los puntos A y B, esto es de acuerdo con el postulado según el cual es posible trazar una línea recta desde cualquier punto a cualquier otro.

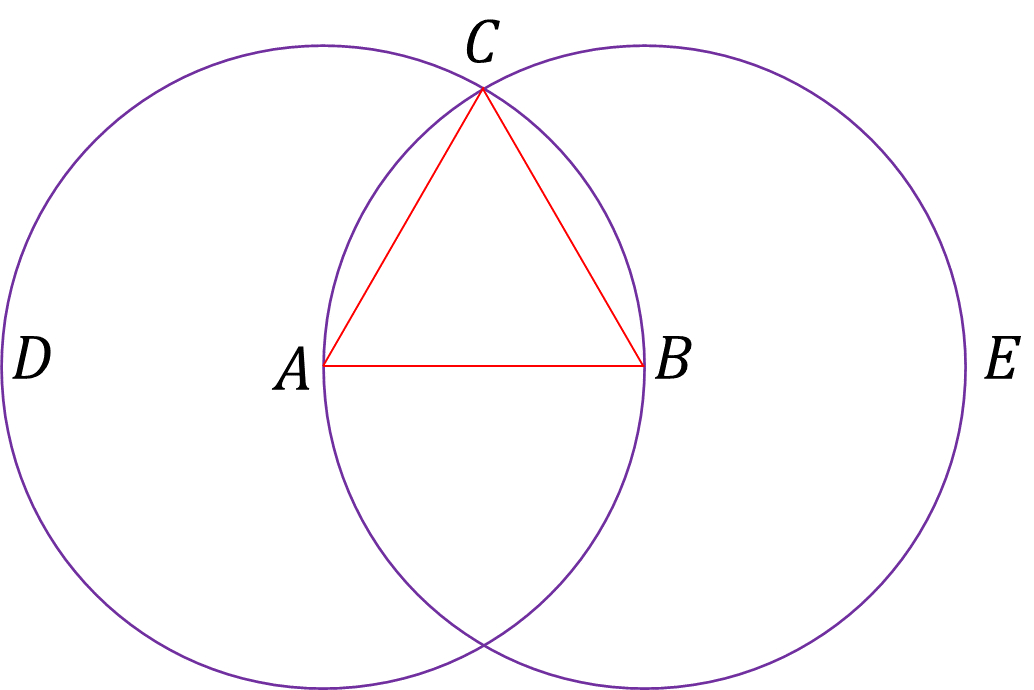
Y puesto que el punto A es el centro del círculo CDB, AC es igual a AB, según la definición de círculo: un círculo es una figura plana rodeada por una línea tal que todas las rectas que inciden sobre ella desde cierto punto interior a la figura son iguales entre sí; considerando esta misma definición, puesto que el punto B es a su vez el centro del círculo CAE, BC es igual a BA; entonces CB es igual a AB.

Según la noción común: las cosas iguales a una misma cosa son también iguales entre sí; CA es también igual a CB; por lo tanto CA, AB y BC son iguales entre sí. Por consiguiente, el triángulo ABC es equilátero y ha sido construido sobre la recta finita dada AB.

Se ha obtenido la afirmación verdadera de que el triángulo trazado es equilátero a partir de definiciones, axiomas y postulados ya enunciados anteriormente. Al razonamiento que se siguió para obtener los teoremas a partir de las verdades evidentes o los axiomas, se le llama demostración.

En el famoso libro “Los elementos”, de Euclides, se encuentran anotadas todas las definiciones, verdades evidentes y las verdades que se desprendían de ellas, llamadas teoremas. Pero no todo lo que se encuentra en el libro lo descubrió Euclides. Algunos contenidos del libro son descubrimientos de los griegos anteriores a él.

Sin embargo, Euclides lo estructuró, se debe a él la elección de los axiomas, el orden de los teoremas y muchas demostraciones. También enunció sólo una pequeña parte de la obra, en total, la también llamada organización de los elementos se compone de 130 definiciones, 5 postulados, 5 nociones comunes, 465 proposiciones, 93 problemas y 372 teoremas, con esto se obtienen las bases de diversos campos temáticos de la matemática griega, como la geometría plana.

Las demostraciones conducen a resultados verdaderos con absoluta seguridad. Otros tipos de razonamiento pueden conducir a errores con mayor facilidad. Por ejemplo, el análisis de casos particulares.

Analiza lo siguiente: ¿es verdad que la expresión general del término enésimo de la sucesión tres, cinco, siete, nueve, once… es “n + 2”?

Una persona, que se base en el análisis de casos particulares, puede responder que sí porque si se sustituye la literal “n” de la expresión “n + 2 (1)”, se obtiene 1 + 2, que da como resultado 3. Como ha obtenido el primer término de la sucesión sustituyendo un valor, la persona concluye que con la expresión dada puede obtener cualquier término.

Sin embargo, la persona no tuvo cuidado en analizar lo que pasaba con todos los casos. Si se analiza la expresión para otros términos de la sucesión, se puede concluir que la expresión es incorrecta.

Específicamente, si se sustituye el valor de “n (2)” se obtiene 2 + 2, que da como resultado 4, y 4 no es el segundo término de la sucesión. Como puedes darte cuenta, el análisis de casos particulares puede conducir a conclusiones incorrectas. En cambio, si una demostración matemática como la que se expuso anteriormente se lleva a cabo adecuadamente, conduce con seguridad a afirmaciones verdaderas, sin necesidad de añadir cualquier otro tipo de verificación.

Ahora, retoma la demostración anterior relacionada con el triángulo equilátero, ¿la demostración proporcionada fue suficiente para saber de que el triángulo que se construyó es equilátero?, ¿se requiere de alguna verificación adicional, como medir los lados del triángulo con una regla? Toma un momento para pensarlo.

En el ejemplo del triángulo, si se hizo bien la exposición, la demostración debe ser suficiente para saber de qué el triángulo que se construyó es equilátero, es decir, que tiene sus tres lados iguales. Nadie se debería sentir tentado a verificar las medidas con una regla graduada.

Con una demostración no se requiere de una verificación empírica, como medir con la regla. Algunos griegos preferían desarrollar demostraciones que involucrarse en los asuntos prácticos o la mecánica. En definitiva, se prefería realizar demostraciones sobre el papel para obtener verdades, que realizar mediciones directamente en el espacio físico.

La obra de “Los elementos” ha tenido muchas aplicaciones a lo largo de la historia. Muchas obras de ingeniería se han construido gracias a ella. Tan grande ha sido el impacto de este libro, que durante más de 2200 años ha sido el libro más usado para enseñar a demostrar a los estudiantes de matemáticas. Incluso en la actualidad, la enseñanza de la geometría está más o menos vinculada con el libro “Los elementos”, sólo ha cambiado el estilo y la presentación, pero no el contenido. (

No obstante, aunque la geometría euclidiana es muy útil, también tiene sus limitaciones. Pero eso lo aprenderás más adelante en tu vida académica.

Con esta información, has concluido la sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Matemáticas, de segundo grado.

El reto de hoy:

Elabora tus notas, considerando las ideas más importantes de la sesión; retoma las actividades planteadas y, sobre todo, anota tus dudas y posibles dificultades para aclararlas más adelante. Si te es posible, investiga la obra “Los elementos” en fuentes de información confiables, ya que esto te servirá a lo largo de tu vida académica.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html