Los histogramas

Los histogramas

Aprendizaje esperado: recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea.

Énfasis: recolectar y registrar datos en histogramas.

¿Qué vamos a aprender?

En esta sesión, conocerás qué es un histograma, por lo que aprenderás a recolectar, organizar y registrar información con este recurso a partir de diversas situaciones.

¿Qué hacemos?

Inicia con la siguiente situación.

¿Sabías que los Juegos Olímpicos número XXXII tendrán lugar en Tokio, Japón? Los Juegos Olímpicos están inspirados en los juegos que se realizaban en la antigua Grecia, en la ciudad de Olimpia, en el siglo VIII antes de nuestra era.

Los Juegos Olímpicos de la era moderna se realizaron por primera vez en Atenas, Grecia, en 1896. Desde entonces, se realizan cada cuatro años en diferentes países del mundo. Se suspendieron en 1916 por la Primera Guerra Mundial, en 1940 y 1944 por la Segunda Guerra Mundial y en 2020 se postergaron debido a la pandemia del COVID-19.

México ha participado de manera regular en varias disciplinas de este evento, entre ellas, el fútbol. ¿Te has preguntado acerca de las edades de los jugadores participantes? ¿Habrá algún límite o podrán participar deportistas de cualquier edad?

En las pasadas olimpiadas número XXXI, celebradas en Brasil en 2016, participaron 18 jugadores de nuestro país en esta disciplina, con las siguientes edades, expresadas en años.

Estos datos pueden servir para comunicar varias ideas, para ello, es posible organizar y presentar esta información con diferentes recursos.

Ahora, contesta las siguientes preguntas:

¿Cómo organizarías las edades de los participantes?

¿Cuántos son los participantes más jóvenes?

¿Cuántos son los participantes de mayor edad?

¿En qué intervalo de edad hay más participantes?

¿Cuántos participantes hay en ese intervalo?

Registra la información en tu cuaderno y represéntenla mediante una gráfica.

Una manera de organizar la información es ordenar los valores, de menor a mayor o viceversa. En este caso, se ordenarán de menor a mayor edad, como se observa a continuación.

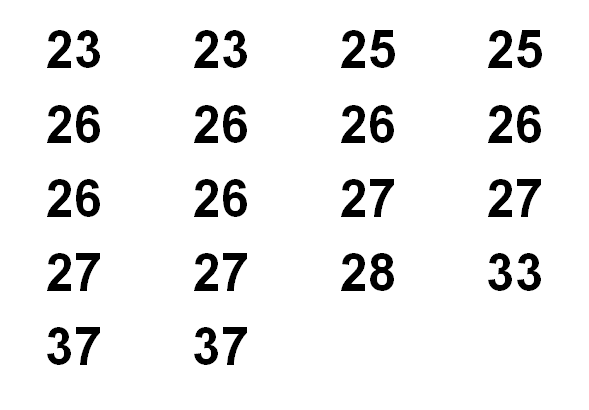
Para representarlos en una gráfica, se pueden agrupar las edades en intervalos, considerando el valor mínimo y el máximo de los datos. En este caso, se organizan en cinco intervalos, que son:

• De 23 a 25 años.
• De 26 a 28 años.
• De 29 a 31 años.
• De 32 a 34 años.
• De 35 a 37 años.

Posteriormente, se organizan en una tabla de frecuencias. De esta manera, los datos quedan de la siguiente forma:

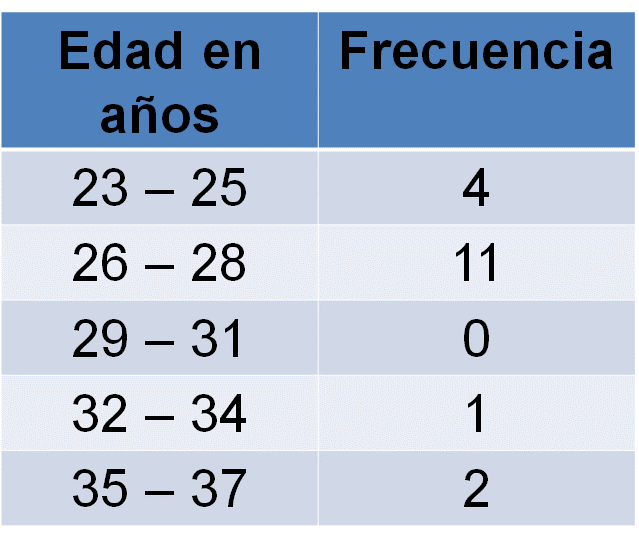
En la primera columna se anotan los intervalos de edad. Recuerda que los intervalos deben ser del mismo tamaño, en este caso, se agrupan en intervalos de tres años. En la segunda columna, se anota cuántos jugadores corresponden en cada intervalo.

Cuando ya se tienen los datos organizados en la tabla de frecuencias, se pueden representar en un histograma. El histograma es un gráfico que permite representar una variable mediante barras, las cuales tienen una superficie proporcional a la frecuencia de los datos. Uno de los usos del histograma es que ayuda a construir otro gráfico, el polígono de frecuencias, que es motivo de estudio de otra sesión.

Para construir el histograma se utilizan dos ejes. En el eje horizontal se representa la variable, que, en este caso, son los intervalos de edad. Al pie de cada barra se anota el intervalo. En el eje vertical se registra la frecuencia, como se muestra en la siguiente imagen.

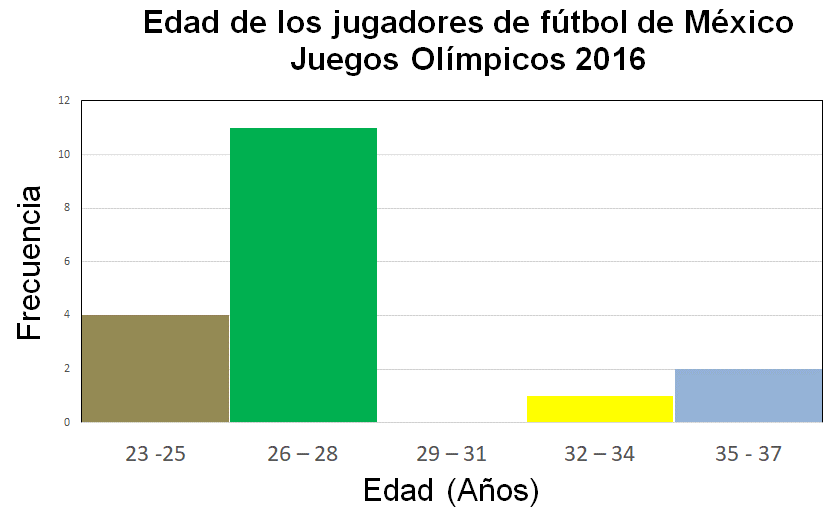
De acuerdo con este histograma, contesta las preguntas anteriores:

• ¿Cuántos son los participantes más jóvenes? Los que se encuentran en el primer intervalo que son 4 y corresponden a las edades entre 23 y 25 años.
• ¿Cuántos son los participantes de mayor edad? Los del último intervalo, que son 2, entre 35 y 37 años.
• ¿En qué intervalo de edad hay más participantes? En el segundo, de 26 a 28 años.
• ¿Cuántos participantes hay en ese intervalo? Hay 11 participantes, como lo muestra la barra más alta.

Como puedes observar en el histograma, hay un intervalo de edades en donde no se reportaron participantes, entre 29 y 31 años. Además de este histograma, ¿has visto otros en algunas fuentes de información?, ¿dónde?, ¿en revistas, periódicos, en libros, en internet?, ¿qué información se mostraba en esos histogramas?

Recuerda hacer anotaciones en tu libreta, ya sean dudas, definiciones u observaciones acerca del tema que se está estudiando.

Analiza la siguiente situación donde estudiarás otros aspectos relacionados con el histograma.

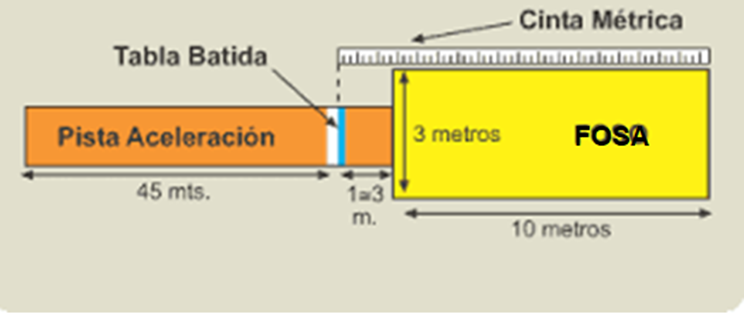
El atletismo es otra de las disciplinas en los Juegos Olímpicos. El salto de longitud es una prueba del atletismo, la cual consiste en una carrera previa que finaliza en una tabla de batida donde se indica el punto para realizar el impulso y caer sobre una fosa de arena.

La distancia del salto se mide desde la tabla de batida hasta la marca hecha por cualquier parte del cuerpo del atleta sobre la arena. El ganador es el que realiza el salto más largo.

En la siguiente imagen se pueden observar algunas partes, y sus medidas, de una pista de aceleración y de la fosa.

A continuación, se presenta información acerca de los mejores saltos de la historia de los Juegos Olímpicos en las diferentes sedes. Representa esta información en un histograma con 5 intervalos.

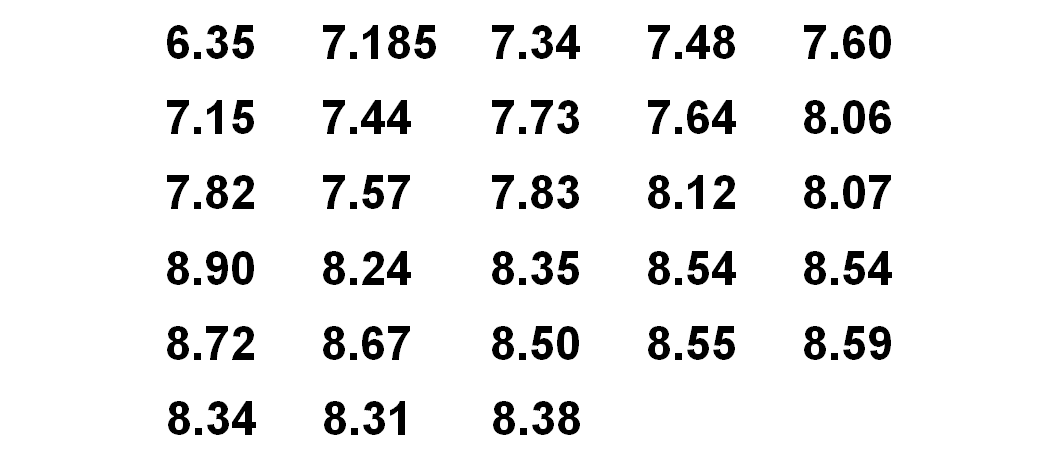
¿Qué harías primero para construir el histograma? Una manera de iniciar es ordenar los datos de menor a mayor. Comienza con 6.35, luego con 7.15, después con 7.185, y así sucesivamente hasta llegar al mayor de los datos que es 8.90. Después, puedes agruparlos en intervalos. Recuerda la importancia de llevar un registro de los procedimientos, dudas y definiciones.

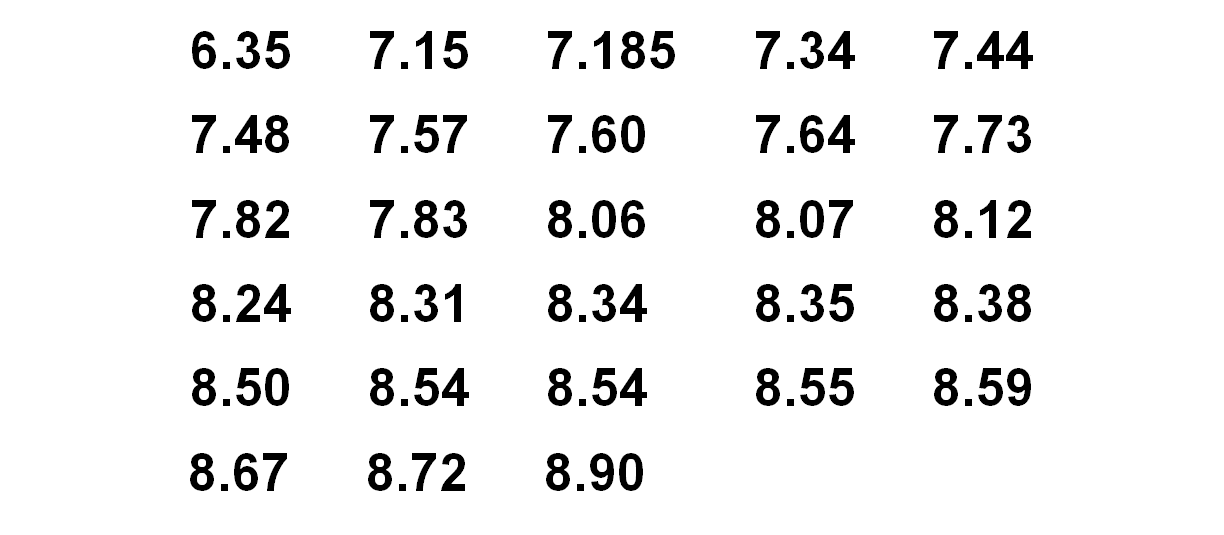
Una vez que tengas los datos ordenados, contesta las siguientes preguntas:

¿Cuál es el dato con menor valor?

¿Cuál es el dato con mayor valor?

¿Cuál es la diferencia entre estos valores?

Con los datos ordenados es más sencillo dar respuesta a las preguntas, el dato con menor valor es 6.35 y el dato con mayor valor es 8.90, recuerda que se está hablando de metros.

La diferencia entre el valor mayor y el menor, es decir, 8.90 menos 6.35 es igual a 2.55. A la diferencia entre el valor mayor y el valor menor de un grupo de datos se le denomina rango.

Continúa con el estudio de este tema. La indicación para este problema es agrupar los datos en 5 intervalos, ¿te has preguntado cómo puedes establecer el tamaño del intervalo?

Para determinar el tamaño del intervalo, se divide el rango entre el número de intervalos. Para este caso vas a organizar la información con 5 intervalos. Entonces, se divide el rango entre cinco, es decir, 2.55 entre 5 igual a 0.51.

Cada uno de los intervalos tiene un límite inferior y un límite superior. Para determinar el primer intervalo, el dato con menor valor es el límite inferior, es decir, 6.35 y el límite superior se obtiene sumando el tamaño del intervalo al límite inferior, es decir, 6.35 más 0.51, que resulta 6.86.

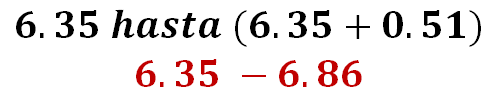
Para el siguiente intervalo, a 6.86 se le suma 0.51, obteniendo 7.37 como límite superior del segundo intervalo.

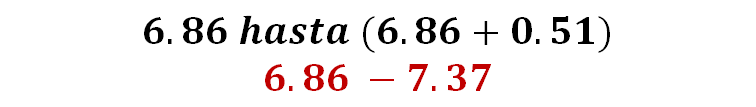
Y así sucesivamente hasta llegar a 8.90 que es el límite superior del último intervalo.

El límite inferior del segundo intervalo, lo vas a considerar como aquellas marcas que sean mayores a 6.86, porque los valores menores o iguales a 6.86 se consideraran en el primer intervalo. Para los siguientes intervalos se considerará el mismo argumento.

Observa la siguiente tabla de frecuencias con cinco intervalos.

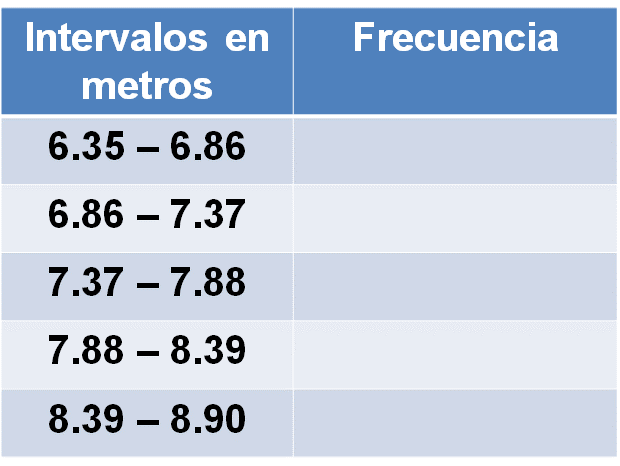
En la primera columna se ubican los intervalos de los saltos de longitud. En la segunda columna se ubican las frecuencias.

El primer intervalo es de 6.35 hasta 6.86 m, el segundo de 6.86 hasta 7.37m, el tercero de 7.37 hasta 7.88m, el cuarto de 7.88 hasta 8.39, y el último intervalo de 8.39 hasta 8.90.

Para establecer la frecuencia se puede recurrir a los datos ordenados y ubicar las medidas de los saltos de acuerdo con cada intervalo. La tabla queda de la siguiente manera:

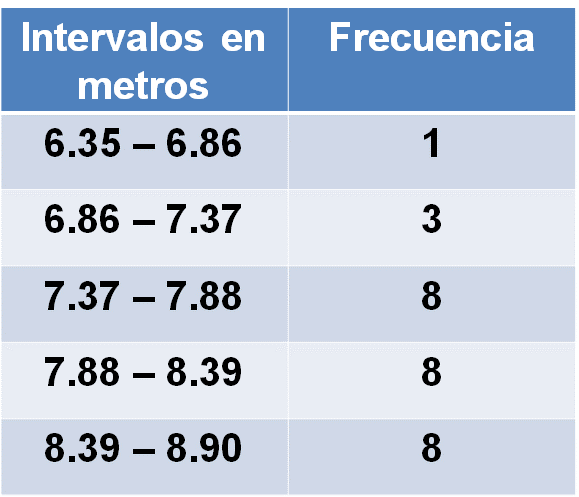
En el primer intervalo sólo se encuentra un salto; en el segundo intervalo se tienen tres saltos; en el tercer intervalo se contabilizan ocho saltos, los mismos que hay en los otros dos intervalos siguientes. Ya que cuentas con la tabla de frecuencias, construirás el histograma.

¿Qué título le pondrías al histograma? La información se refiere a las mejores marcas de salto de longitud en Juegos Olímpicos. Observa cómo quedaría el histograma.

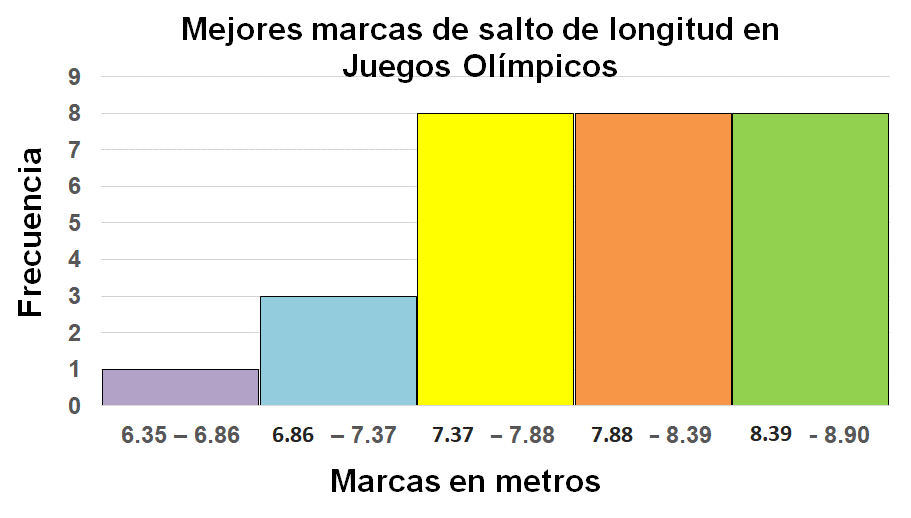
En el eje vertical se registran las frecuencias, en este caso, se registra de cero a nueve. En el eje horizontal se registran los cinco intervalos, el nombre que se le asigna es “Marcas en metros”. Después, se determina la altura de la barra de cada intervalo de acuerdo con su frecuencia.

Has concluido la construcción el histograma. Para continuar, contesta las siguientes preguntas con base en la información del histograma y registra tus respuestas en tu cuaderno.

¿Cuál es el salto de mayor longitud registrado en la historia de los Juegos Olímpicos?

¿Cuántos Juegos Olímpicos se han celebrado hasta la fecha?

¿En qué intervalo se sitúan los atletas que registraron el mejor salto?

Si en los próximos Juegos Olímpicos un atleta desea rompe el récord mundial, ¿es posible agrupar el dato con los intervalos que se han establecido?

Ahora, verifica tus respuestas.

¿Cuál es el salto de mayor longitud registrado en la historia de los Juegos Olímpicos? El salto de mayor longitud es de 8.90 metros. Esto se observa en el límite superior del último intervalo.

¿Cuántos Juegos Olímpicos se han celebrado hasta la fecha? Para dar respuesta a esta pregunta se puede observar el número de datos. En este caso son 28, es decir, desde 1896 hasta el 2016 se han celebrado 28 eventos de Juegos Olímpicos, que son los 28 datos que se tienen.

¿En qué intervalo se sitúan los atletas que registraron el mejor salto? Como se observa en el histograma, el mejor salto se encuentra en el último intervalo, de 8.39 a 8.90m.

Si en los próximos Juegos Olímpicos un atleta desea romper el récord mundial, ¿es posible agrupar el dato con los intervalos que se han establecido? No es posible integrarlo a los intervalos ya establecidos, porque para mejorar la marca, tendría que dar un salto mayor a 8.90 metros, que es el límite superior del último intervalo.

Compara la organización de los datos y el histograma que se obtuvo con lo hiciste, y escribe en tu cuaderno las diferencias y las semejanzas que se observan.

Continúa con la construcción de los histogramas, así como con el análisis de la información que se presenta en ellos. Para ello, aborda otra situación.

En México, cada diez años se realiza un Censo de Población y Vivienda. En 2020 se realizó el más reciente. ¿Recuerdas haber recibido en casa al entrevistador?

Ellos visitaron cada una de las viviendas para obtener información, contar a la población que vive en México e indagar sobre sus principales características demográficas, socioeconómicas y culturales.

Uno de los datos que aportó el censo de 2020 se refiere al promedio de personas que ocupan una vivienda en la República Mexicana. Observa la información.

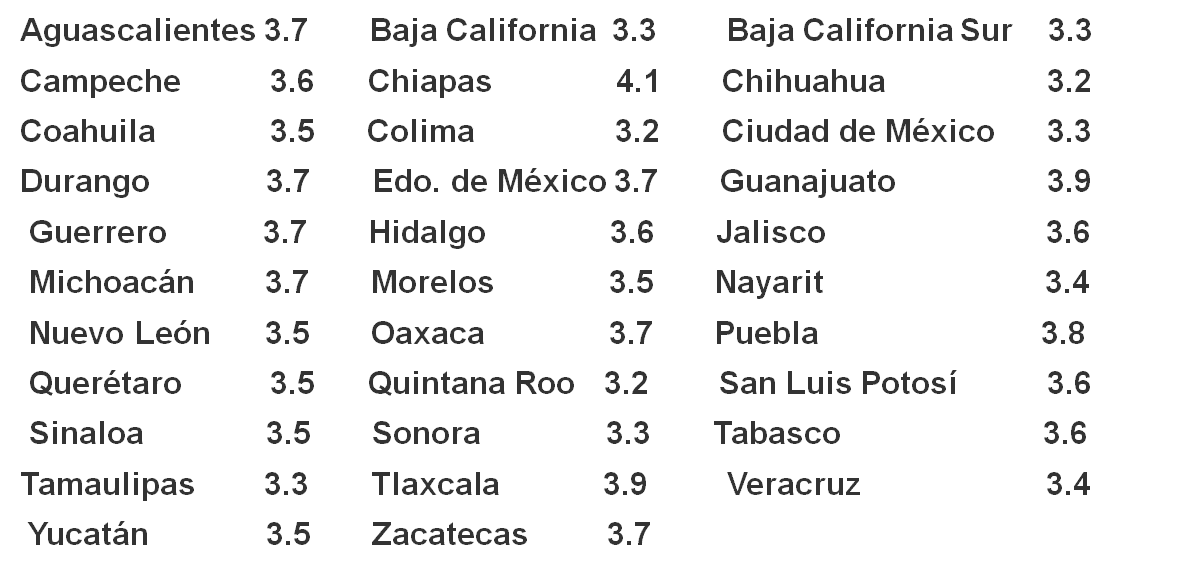
Ahora, construye un histograma con 6 intervalos para mostrar los datos anteriores. Después, lee las siguientes afirmaciones y anota falso o verdadero, según corresponda. Justifica tus respuestas.

Puedes iniciar por organizar los datos de menor a mayor. Para facilitar el manejo de la información sólo vas a utilizar los valores numéricos sabiendo que corresponden al promedio de habitantes por vivienda. Entonces, se ordenan de la siguiente manera:

Para establecer el tamaño del intervalo, necesitas conocer el rango, para ello, calcula la diferencia entre el límite superior y el límite inferior.

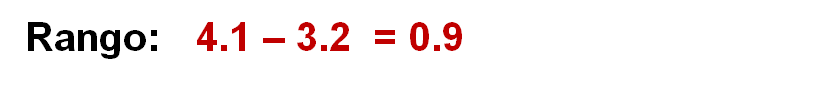
Como serán seis intervalos, calcula el cociente del rango, 0.9 entre 6, arroja un resultado de 0.15, éste será el tamaño de cada intervalo.

Ahora puedes construir la tabla de frecuencias, en la primera columna se colocan los intervalos sobre el promedio del número de personas que habitan una vivienda y en la segunda columna se anota la frecuencia. Haciendo el conteo, queda de la siguiente manera:

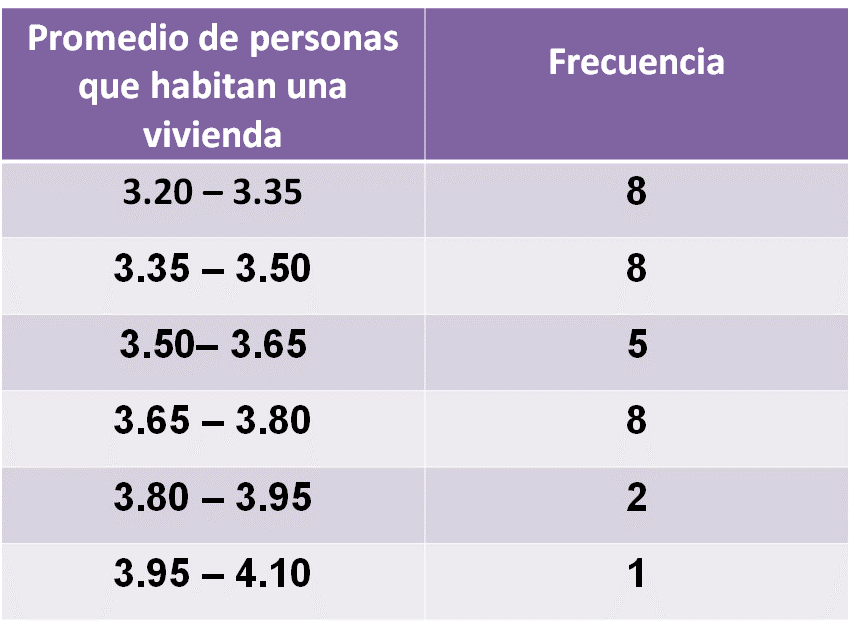
El primer intervalo es, de 3.20 hasta 3.35, el segundo, de valores mayores de 3.35 a 3.50, el tercero de 3.50 hasta 3.65, el cuarto intervalo de valores mayores de 3.65 hasta 3.80, el quinto intervalo de valores mayores de 3.80 hasta 3.95, y el último intervalo de valores mayores de 3.95 hasta 4.10.

Las frecuencias son: para el primer intervalo, 8 estados de la república; en el segundo intervalo se encuentran también 8 estados; en el tercer intervalo hay 5 estados; en el cuarto intervalo se tienen 8 estados; en el quinto, 2 estados; y en el sexto, 1.

Con esta información puedes continuar con la construcción del histograma. Observa cómo queda:

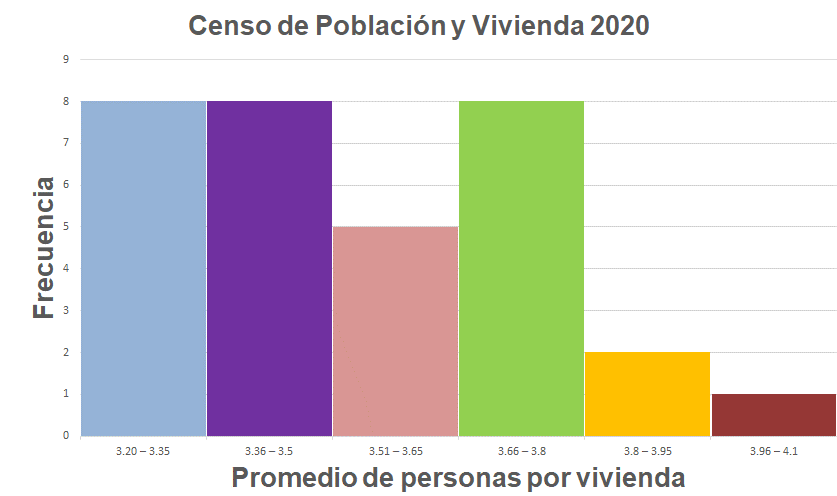
Ahora, verifica tus respuestas. Las afirmaciones, son las siguientes:

• En tres estados de la República Mexicana el promedio de habitantes por vivienda es de aproximadamente cuatro personas. Esta afirmación es falsa, ya que, de acuerdo con los datos que se observan en la gráfica, sólo un estado del país se encuentra representado en ese intervalo.
• Existen tres grupos de datos formado por 8 estados, cada grupo corresponde a un intervalo diferente de números de personas que viven en una misma casa. Esta afirmación es verdadera, se identifican tres intervalos con 8 estados cada uno, el primero, el segundo y el cuarto intervalo.
• En 5 estados de la República, en promedio cada vivienda es habitada entre 3.8 y 3.95 personas. Es falso, en ese intervalo de 3.8 a 3.95, se encuentran sólo dos estados.
• No se identificaron viviendas con menos de 3.20 habitantes en promedio en ningún estado de la República Mexicana. Es verdadero, no existen datos en la gráfica con valores menores al primer intervalo de 3.20 a 3.35.
• Cinco estados del país se encuentran en un intervalo de 3.65 a 3.8 personas por vivienda. Es falso, los estados que se encuentran en este intervalo son 8.

Un histograma permite observar información de un conjunto de datos, pero puede ocurrir que exista otra información que no sea posible mostrar en el gráfico.

Ahora, contesta lo siguiente:

• ¿Piensas que sea conveniente hacer intervalos para un conjunto de 6 datos?, ¿y para uno de 50 datos?
• ¿Para qué situaciones es conveniente organizar la información en un histograma?
• ¿Para qué situaciones piensas que no sería pertinente construir un histograma?

Con esto has finalizado la sesión, dedicada a recolectar y registrar datos en histogramas.

Recuerden que éste es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

El reto del hoy:

Consulta tu libro de texto de matemáticas y resuelve los problemas o ejercicios sobre el tema de esta sesión, los histogramas, para que recolectes y registres datos con este recurso.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html