Análisis de las medidas de tendencia central y del rango.

Análisis de las medidas de tendencia central y del rango.

Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) y el rango en un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión.

Énfasis: analizar las propiedades de la media aritmética y de la mediana.

¿Qué vamos a aprender?

Aprenderás a interpretar las medidas de tendencia central y el rango; también analizarás las propiedades de la media aritmética, al igual que la mediana.

Es muy importante tu participación en las actividades que se proponen; para ello, te recomendó que lleves un registro de las ideas principales, las preguntas, retos y reflexiones que te surjan.

¿Qué hacemos?

Comenzarás con un pequeño juego lógico matemático. Se tienen 10 puntos y 5 líneas.

La intención del juego es colocar 4 puntos en cada una de las 5 líneas, las cuales pueden unirse, encimarse o cruzarse, pero con la condición de que en cada línea queden 4 puntos. No se puedes agregar puntos; es decir únicamente deben ser 10 y ningún punto más.

¿Lograrás resolver este reto?

Para iniciar la sesión, identificarás las características de cada una de las medidas de tendencia central, junto con los procedimientos correspondientes a cada una de ellas.

Antes, es importante que sepas que las medidas de tendencia central son la moda, media aritmética o promedio y mediana. Éstas son medidas estadísticas que, en un solo valor, representan una característica de un conjunto de datos.

Comenzarás con la media aritmética o promedio que es una medida de tendencia central. Se representa con una equis, sobre la cual se coloca una línea y se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado entre el número total de los datos que conforman al conjunto.

La media aritmética o promedio es una de las llamadas medidas de tendencia central. Si cambiaras todos los datos del conjunto por el valor de la media aritmética o promedio, la sumatoria del total de los datos, sería la misma que la sumatoria de los valores originales.

Por ejemplo, tu, al final de cada periodo de evaluación, recibes el promedio obtenido, que es la suma de las evaluaciones de cada materia, dividida entre el total de ellas.

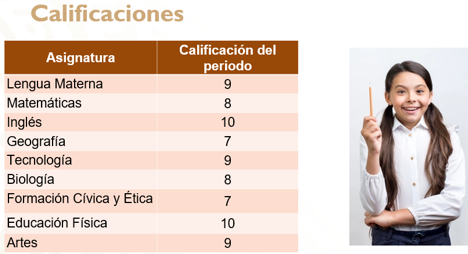
Suponiendo que una estudiante de primer grado obtuvo las siguientes notas en cierto periodo, calculemos la media aritmética o promedio que obtuvo.

Lengua materna 9, matemáticas 8, inglés 10, geografía 7, tecnología 9, biología 8 formación cívica y ética 7, educación física 10 y artes 9.

Para poder obtener la media aritmética o promedio, habrá que sumar todas las calificaciones y dividirlas entre el total de asignaturas, que son 9.

Primero sumas:

9 + 8 + 10 + 7 + 9 + 8 + 7 + 10+ 9 y divides el resultado entre 9. Así obtienes 77 entre 9.

77 entre 9, es aproximadamente igual a 8.55

Por lo tanto, la media aritmética o promedio de la alumna, al concluir el periodo, es de: 8.5.

Ahora, analiza a la mediana. La mediana es el valor central de un conjunto de datos ordenados de menor a mayor o de mayor a menor; por lo que hay el mismo número de datos antes de la mediana y después de ella. Se representa por una x con una tilde (curvo) arriba o por “Me”

La mediana está “a la mitad” de un conjunto de datos ordenados, por eso hay el mismo número de valores antes de la mediana y después de ella. Cuando el número de datos numéricos de un conjunto es par, no existe un dato que se ubique exactamente a la mitad de la lista ordenada, por lo que la mediana se calcula como el promedio de los dos valores centrales.

Cuando el número de datos numéricos es impar, el dato que se ubique exactamente a la mitad de la lista ordenada será la mediana.

Continuando con la situación de la estudiante de primer grado, obtén la mediana de sus calificaciones del periodo.

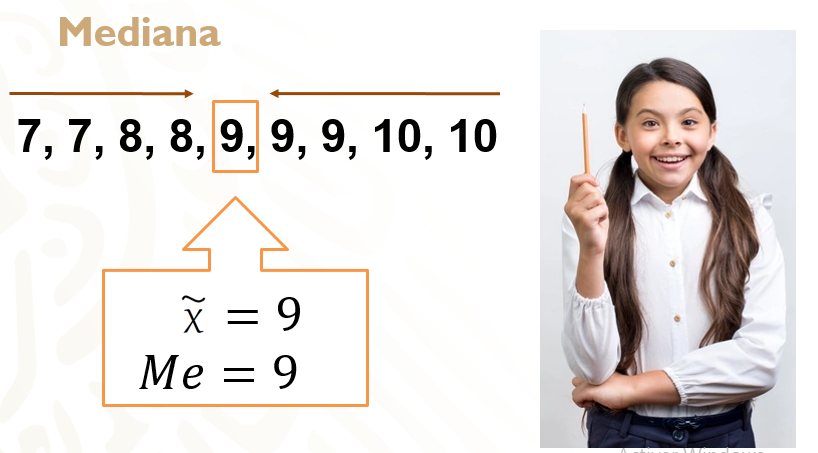
Para comenzar, debes ordenar los datos de mayor a menor o viceversa; en este caso, los acomodarás de menor a mayor incluyendo todas las calificaciones, el orden sería el siguiente:

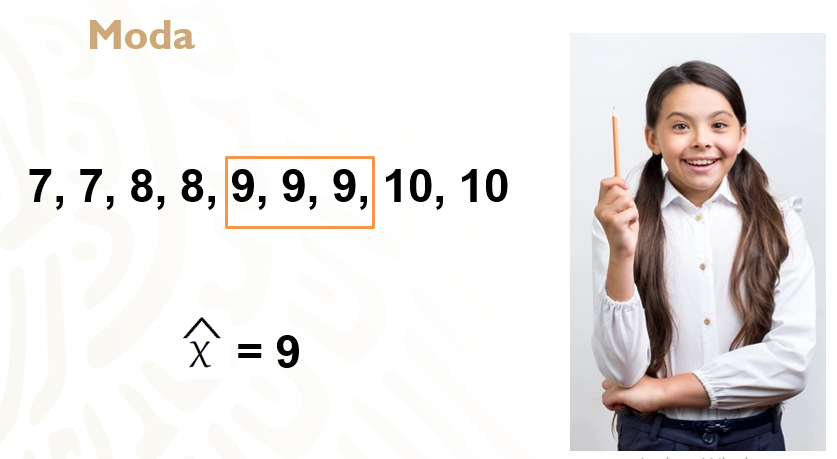
7, 7, 8, 8, 9, 9, 9, 10 y 10

Es importante resaltar que, aunque los datos se repitan, no se debe omitir ninguno.

Al ser un número impar, el dato que está justo al centro de los datos acomodados será la mediana; es decir, 9.

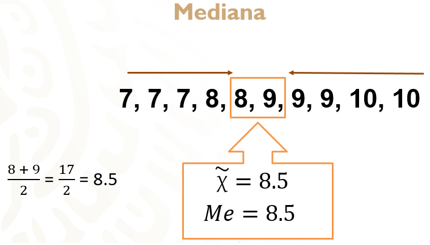
Para ejemplificar un caso en el que el número de valores sea par, consideremos que hay una materia extra y que su calificación en ella fue 7. Por lo tanto, la lista ordenada de datos queda de la siguiente manera:

7, 7, 7, 8, 8, 9, 9, 9, 10 y 10

Ahora tienes un número par del conjunto de datos, lo cual implica que debes sacar la media aritmética de los dos valores centrales. En medio de la lista, quedan los valores 8 y 9; así que debemos de sumar 8 + 9 = 17 y dividir entre 2, esto es igual a 8.5.

La tercera medida de tendencia central que verás es la moda. La moda es el dato que más aparece o que tiene mayor frecuencia. Si un grupo de datos tiene dos modas, se dice que es bimodal, y si son más de dos, es multimodal. Se representa con una x y un símbolo arriba o como Mo.

Siguiendo con la situación de la alumna de primer grado, observa sus calificaciones ya ordenadas y elige la que aparece más veces. En este caso, el valor que se repite mayor número de veces es 9

Si tomas en cuenta la calificación de la materia extra, que fue 7, el conjunto de datos ordenados queda de la siguiente manera:

7, 7, 7, 8, 8, 9, 9, 9, 10 y 10

Para este conjunto, puedes identificar dos elementos que se repiten la misma cantidad de veces, son el siete y el nueve. Este conjunto de datos se considera bimodal y la moda en este caso es 7 y 9.

Ahora, analiza al rango, que es una medida de la dispersión de un conjunto de datos, e indica qué tan distantes están entre sí, una vez ordenados, el primer dato del último dato. Un rango alto significa que los datos son numéricamente muy distintos entre sí; en cambio, un rango bajo indica que los datos son muy parecidos entre sí.

El rango de un conjunto de datos es la diferencia entre el mayor y el menor de ellos, por lo que se calcula con la siguiente operación.

Rango = Dato mayor – Dato menor

Retomando el problema de la estudiante de primer grado, calcula el rango de sus calificaciones; es decir, tomarás la máxima calificación que se obtuvo, 10, y le restarás la mínima calificación, que en este caso es 7; entonces el rango = 10 – 7 = 3

El rango para este caso es: 3.

Sabiendo que la media de las calificaciones de la alumna fue 8.5, que la mediana fue 9 y que la moda fue 9. ¿Qué medida consideras que pueden ser más representativa del conjunto de datos?

Cabe mencionar que la media aritmética es muy sensible a los datos atípicos o extremos, mientras que la mediana no se afecta por estos valores.

El valor atípico de un conjunto de datos es aquel valor que es distante de todos los demás, lo que provoca que la media se vea afectada.

Analiza el siguiente problema.

Se eligieron 30 familias al azar, a las cuales se les preguntó sobre su gasto mensual de luz.

El gasto de cada una en pesos fue el siguiente: 220, 540, 320, 760, 870, 940, 450, 320, 520, 420, 110, 320, 320, 530, 420, 430, 430, 650, 840, 420, 320, 220, 790, 950, 340, 540, 1100, 350, 820 y 120.

Para iniciar a trabajar con los datos proporcionados en el problema propuesto, es indispensable ordenarlos de mayor a menor, o viceversa. En este caso, se organizan de menor a mayor de arriba hacia abajo en una tabla.

Con base en los datos que nos proporciona el problema, calcula la media, la mediana, la moda y el rango de los datos.

¿Cómo consideran que es la dispersión de los datos?

¿Cuántos datos hay antes y después de la media aritmética o promedio?

Si tuvieras que elegir un valor que represente al conjunto de los datos, ¿elegirías a la media aritmética? ¿Por qué?

Para poder responder las preguntas planteadas, calcula las medidas de tendencia central y el rango.

Una vez ordenados los datos, puedes comenzar a calcular las medidas de tendencia central solicitadas.

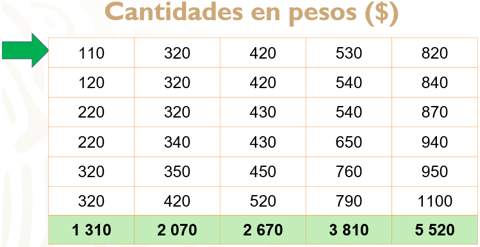
Trabaja realizando, primero, las sumas parciales de cada columna. En la última fila, se tienen las sumatorias parciales de los datos de cada columna.

En la primera columna, se obtienen 1 310 pesos; en la segunda, 2 070 pesos; en la tercera, 2 670; en la cuarta, 3 810; y, por último, 5 520.

Después, realiza la suma de los resultados parciales obteniendo, de esta forma, la suma total de datos de 15 380 pesos.

Por último, divides la suma total entre el número de datos, en este caso son 30 familias; y, así, obtienes la media aritmética o promedio que es de 512.66 pesos.

Para continuar y obtener la mediana, debes considerar el número total de datos, 30, que es un número par, lo que significa que tienes dos números centrales; es decir, en la posición 15 y 16, debes sumar ambos términos y dividirlos entre dos.

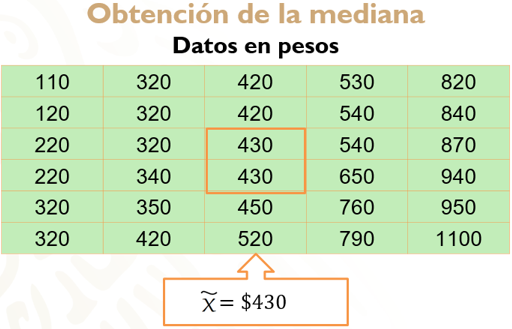
Sin embargo, al observar ambas posiciones, te das cuenta de que son del mismo valor, por lo que, para este caso en particular, no hace falta realizar la operación.

Por lo tanto, la mediana será: 430 pesos.

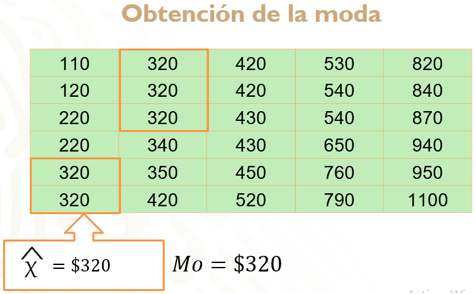
Para encontrar la moda, debes revisar cuál de los valores de la tabla es el que más se repite o el de mayor frecuencia. Si revisas cada uno de los valores, el valor que más veces aparece o se repite es el 320; por lo tanto, la moda es: 320 pesos.

Para concluir, se debe obtener el rango de los datos. Gracias a que los datos que están ordenados se pueden identificar que el valor máximo es 1 100 y el mínimo 110. La diferencia de ambos da como resultado 990. Por lo tanto, 990 pesos es el rango de este problema.

Para la pregunta: ¿Cómo consideras que es la dispersión de los datos? Al observar que el valor del rango obtenido es de 990 pesos, puedes ver que los datos se encuentran muy dispersos o lejanos entre sí.

¿Cuántos datos hay antes y después de la media aritmética o promedio?

Sabiendo que la media aritmética fue de 512.67 pesos ¿cuántos datos después o mayores a ésta hay?

Con los datos ordenados de menor a mayor, marca, con color verde, los valores que están antes o que son menores a512.67 pesos y con azul los que están después o son mayores. Ahora, basta con contar el número de datos en verde y en azul.

Al contar los datos en verde y en azul podemos responder que hay 17 valores antes o menores que 512.67 pesos y 13 valores después o mayores a la media aritmética o promedio. Y por la amplitud del rango, podemos ver que muchos datos están muy lejanos de la media.

Lo anterior lleva a dar respuesta a la pregunta;

Si tuvieras que elegir un valor que represente al conjunto de los datos, ¿elegirías a la media aritmética? ¿Por qué?

Es común creer que la media aritmética o promedio sería el adecuado como respuesta, pero ¿realmente sirve para este caso?

Anteriormente, se mencionó que, cuando los datos se encuentran bastante alejados de la media aritmética o promedio, ésta se ve afectada y su valor no representa al conjunto de datos. En esos casos, pueden utilizarse la mediana o la moda, que no se ven afectadas por la dispersión de los datos.

Entonces, como respuesta a la pregunta, la media aritmética no representa a los datos; se menciona su valor y se dice que los valores oscilan entre el valor mínimo y el valor máximo. Con este problema, has aprendido a interpretar las medidas de tendencia central.

El reto de hoy:

En una fábrica de jugos, se llenan las botellas con una máquina que ajusta el contenido para que sea de 350 ml. Si la máquina pone de más, la fábrica pierde dinero; y si pone de menos, podría ser multada por la Procuraduría del Consumidor: No hay seguridad de que la máquina ponga exactamente la misma cantidad en todas las botellas. Para verificar que la máquina funciona correctamente, se hace una muestra de 50 jugos que arroja que la inmensa mayoría de las botellas tienen poco más o poco menos de 350 ml.

Para este problema debes obtener:

El valor de la moda, el valor de la mediana y calcular la media aritmética.

Así como los valores mínimo y máximo y calcular el rango.

A continuación, aparece una tabla con los valores de la medida del contenido en mililitros de una muestra de 50 jugos. Observa en la tabla que los valores no tienen un orden establecido.

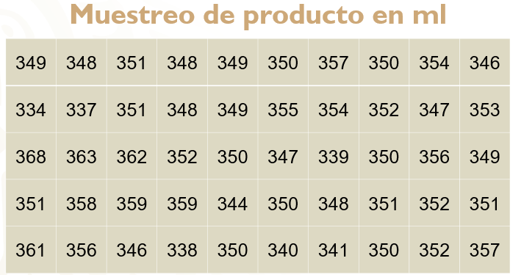
Para resolver el problema, inicia ordenando los datos de menor a mayor. Puedes usar una tabla de frecuencias, para evitar repetir los mismos datos y sólo contabilizar el número de veces que se repite, cada uno. En la primera columna, se colocan los valores de las botellas de jugo en mililitros; y en la segunda columna, la frecuencia o veces que se repite esa medida.

Para calcular cada uno de los valores sugeridos, el acomodo realizado te sirve de ayuda.

Por ejemplo, para encontrar el valor mínimo y máximo, basta con observar en la tabla de frecuencia creada ambos términos.

Siendo 334 ml el valor mínimo y 368 ml el valor máximo, puedes obtener el rango que es 34.

Continuando con el problema, obtén el valor de la moda. Es necesario recordar que la moda es el valor que más veces se repite o el de mayor frecuencia.

Nuevamente, la tabla de frecuencias creada te servirá para dar respuesta a lo solicitado. Observa que el valor en mililitros de mayor frecuencia es: 350. Por lo tanto, la moda es 350 ml.

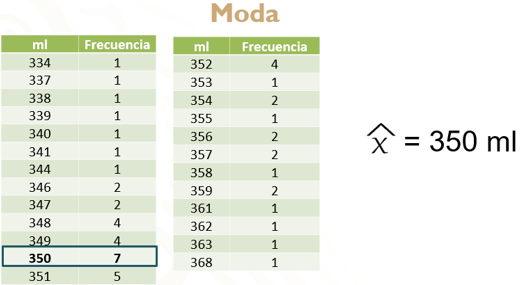
Ahora, para encontrar el valor de la mediana, debes recordar que, al ser 50 datos en la tabla; es decir, una cantidad par, debes encontrar los datos centrales en la posición 25 y 26, para sumarlas y dividirlas entre dos. En la tabla de frecuencias puedes ver que hasta 349 ml hay 19 datos y, como para 350 ml la frecuencia es siete, quiere decir que ahí están los datos del 20 al 26. Las posiciones 25 y 26 corresponden al valor 350. Al ser el mismo valor no hay necesidad de sumar y dividir. Por lo tanto, puedes afirmar que la mediana es igual a 350 mililitros.

Por último, debes calcular la media aritmética. Para realizarlo, debes recordar que hay que sumar cada uno de los valores de la tabla original y dividirlo entre el total de datos; es decir, 50.

Si aprovechas la tabla de frecuencia inicial, podrías multiplicar cada uno de los valores por su frecuencia, obteniendo el total parcial de cada dato para después sumarlos.

La tabla muestra la suma parcial de cada valor; así que podrás sumar todos los productos encontrados y obtener el total de los datos. Al realizar la suma correspondiente, el resultado es 17 532.

Sólo faltaría dividir 17 532 entre el total de datos; es decir, entre 50. Al resolver la división, el valor de la media es 350.64 ml.

Ya que calculaste las medidas de tendencia central y que conoces el rango de los datos, ¿puedes decir que la media aritmética es un dato representativo del contenido de jugo en las botellas?

Al ver el rango, puedes ver que la dispersión entre los valores es muy poco; por lo que puedes considerar a la media aritmética como un valor representativo del conjunto de datos.

¿Qué pasaría con la media aritmética si dentro de los datos hubiera un valor atípico?

Supón que, dentro de los valores de la tabla de llenado de jugos, en lugar del envase de 334 ml hay uno con 50 ml.

Si te piden calcular la media aritmética, considerando el valor atípico, la sumatoria de todos los elementos daría 17 248; esta cantidad se debe dividir nuevamente entre 50 dando como resultado 344.96 ml

Si calculas la diferencia entre la primera media y la segunda, restaríamos 350.64-344.96 = 5.68 ml.

Si consideras esta media aritmética como válida al multiplicar ese error promedio de llenado por 1 000 botellas, tendrías una perdida y/o ganancia de 5 680 ml. Parece poco, pero al ser evaluados por la Procuraduría del Consumidor, se deben respetar los límites o normas de llenado establecidos.

Sin embargo, si realizas el cálculo de la media aritmética o promedio sin considerar el valor atípico; es decir, el valor de 50 ml, en lugar de dividir entre 50 datos lo harás entre 49, quedando: 17 198 entre 49 = 350.97 ml

La diferencia con la media aritmética original sería de 350.97 - 350.64 = 0.33 ml. Si multiplicas este error promedio de llenado por 1000 botellas, tendrías una pérdida o ganancia de 330 ml, reduciendo el error de llenado en un 94 %; de ahí la importancia de considerar o no un valor atípico.

Por otro lado, los valores de la moda y la mediana no se vieron afectados con el valor atípico, por lo que servirían para hablar del comportamiento de los datos en general.

Ahora que ya conoces las medidas de tendencia central, media aritmética o promedio, moda y mediana, además de rango y valor atípico, podrán ocuparlas en el análisis de listas de datos estadísticos, considerando lo realizado durante la resolución de los problemas propuestos.

Una pista para resolver el juego sugerido al inicio de la sesión: en la unión interna de los vértices o diagonales de un polígono regular podrías encontrar la respuesta.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html