Triángulos congruentes

Triángulos congruentes

Aprendizaje esperado: analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina los criterios de congruencia de triángulos.

Énfasis: establecer los criterios de congruencia.

¿Qué vamos a aprender?

Analizarás los datos mínimos necesarios para la construcción de triángulos congruentes, a través del planteamiento de algunas situaciones cotidianas.

¿Qué hacemos?

En esta sesión será de gran utilidad tu cuaderno y tu juego de geometría; ya que aprenderás a identificar la información mínima requerida para trazar triángulos congruentes.

Analiza la siguiente situación.

Sofía, Ana, Fernando y José construyeron banderines con forma triangular para el grupo de animación de su escuela, cada uno hizo uno.

Las medidas de los banderines de cada uno de ellos son las siguientes:

Banderín 1, lo realizó Sofía con las medidas: 20.5 cm, un ángulo de 75 grados, 34 cm y 39.7 cm.

Banderín 2, lo realizó Fernando con las medidas: 44.6 cm, un ángulo de 75 grados, 20.5 cm y 34 cm.

Banderín 3, lo realizó Ana con las medidas: 20.5 cm, 34 cm y un ángulo de 75 grados.

Banderín 4, lo realizó José con las medidas: 20.5 cm, un ángulo de 75 grados, 44.6 cm y 39.7 cm.

De acuerdo con los datos que se mostraron, ¿puedes establecer si los cuatro banderines son congruentes? Observa con atención los banderines.

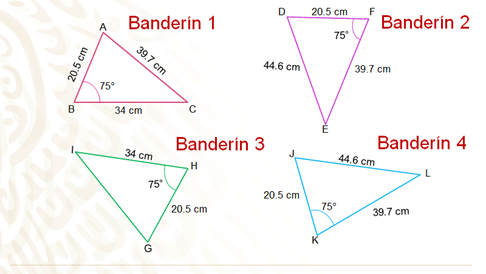
En la imagen se pueden observar los cuatro banderines, el primero de ellos está de color rojo, el lado AB mide 20.5 cm, el ángulo B 75 grados, el lado BC mide 34 cm y el tercer lado, AC, 39.7 cm.

El segundo banderín es de color morado, el ángulo F mide 75 grados, el lado DF mide 20.5 cm, el lado DE mide 44.6 cm y el tercer lado, EF, mide 39.7 cm.

El tercer banderín es de color verde, en donde el ángulo H mide 75 grados, el lado GH mide 20.5 cm y el lado HI mide 34 cm.

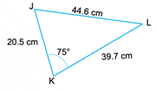
El cuarto banderín tiene las siguientes medidas: el lado JK 20.5 cm, el ángulo K 75 grados, el lado KL mide 39.7 cm y el lado JL 44.6 cm.

¿Puedes dar respuesta a la primera pregunta? ¿Los cuatro banderines son congruentes?

Posiblemente respondiste que sí porque las medidas de los lados que muestran los banderines son las mismas y tienen el mismo ángulo, pero eso no es del todo cierto.

En matemáticas existen algunos criterios que permiten establecer si dos triángulos son congruentes ocupando un mínimo de datos y se les conoce como criterios de congruencia de triángulos. Recuerda que las figuras congruentes, son aquellas cuyos lados y ángulos correspondientes miden lo mismo.

Se sugiere poner atención a la siguiente imagen y anotar la información en tu cuaderno.

Los criterios de congruencia de triángulos, son tres:

El primer criterio lado, lado, lado y se escribe de manera simplificada como LLL y dice que: “dos triángulos son congruentes si sus tres lados correspondientes son iguales”.

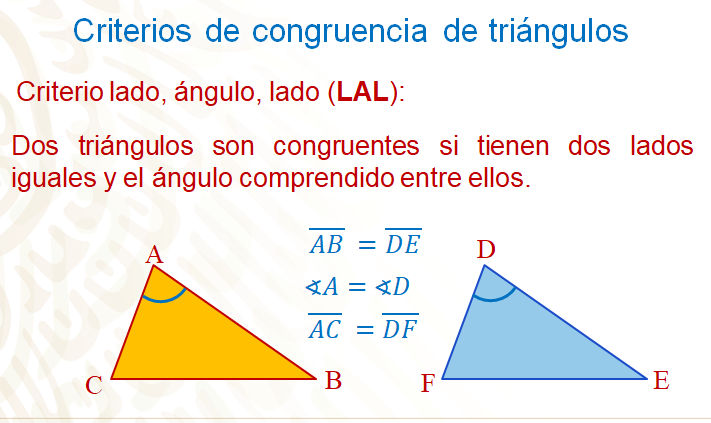
El segundo criterio es lado, ángulo, lado, se simplifica como LAL, y dice que: “dos triángulos son congruentes si tienen dos lados iguales y el ángulo comprendido entre ellos”.

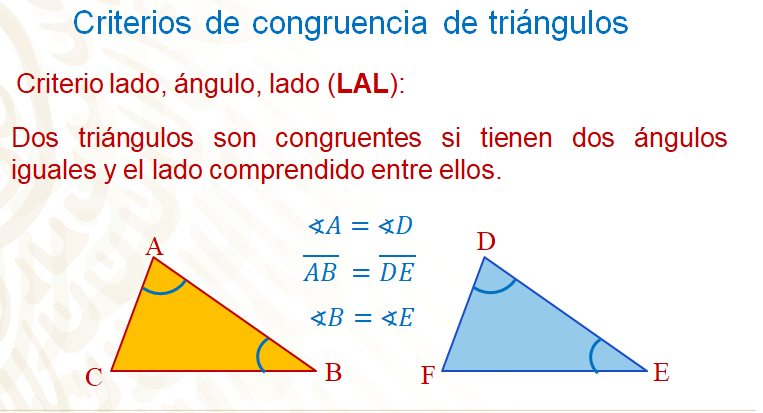
El tercer criterio es ángulo, lado, ángulo que se indica como ALA y dice que: “dos triángulos son congruentes si tienen dos ángulos iguales y el lado comprendido entre ellos, también es igual”.

Con esta información ya puedes dar respuesta a la primera pregunta. ¿Los cuatro banderines son congruentes?

Primero, compara el banderín 1 con el banderín 2 para determinar si estos son iguales; es decir, congruentes, aplicando los criterios anteriores.

Dado que los banderines cuentan con las medidas de sus tres lados, podrás utilizar el primer criterio LLL (lado, lado, lado), el cual menciona que dos triángulos son congruentes si sus tres lados correspondientes son iguales.

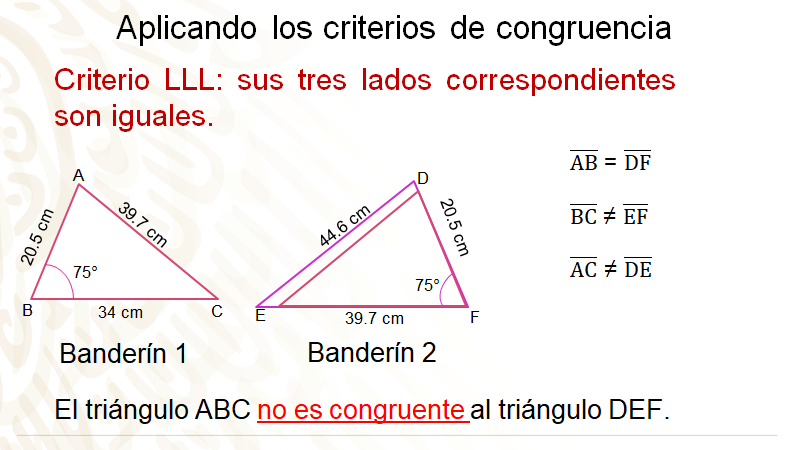
Analiza los lados de los dos triángulos, compara el segmento AB del banderín 1 con el segmento DF del banderín 2. Se puede observar que ambos miden lo mismo 20.5 cm, por lo que estos lados son iguales.

Realiza lo mismo con el segundo lado de ambos triángulos. Del primero es el segmento BC, del segundo es el segmento EF, por ser los otros lados del ángulo de 75 grados; visualiza en la imagen que el segmento BC mide 34 cm, mientras que el segmento EF mide 39.7 cm, por lo que estos lados no miden lo mismo.

Por último, analiza el tercer lado de ambos triángulos. Del primero es el segmento AC que mide 39.7 cm con el segmento del segundo triángulo DE que mide 44.6 cm. Como se puede observar, estos lados no son iguales. Por lo que se puede determinar que el banderín 1 y 2 no son congruentes.

Verifica si el banderín 1 y el banderín 3 son congruentes; para ello aplica, de igual forma, los criterios de congruencia.

Observa la siguiente imagen de los banderines 1 y 3, el triángulo uno cuenta con las tres medidas de sus lados y un ángulo, el tercer triángulo cuenta con dos medidas de sus lados y un ángulo, por lo que puedes utilizar el segundo criterio LAL; el cual menciona que dos triángulos son congruentes, si tienen dos lados iguales y el ángulo comprendido entre ellos también es igual.

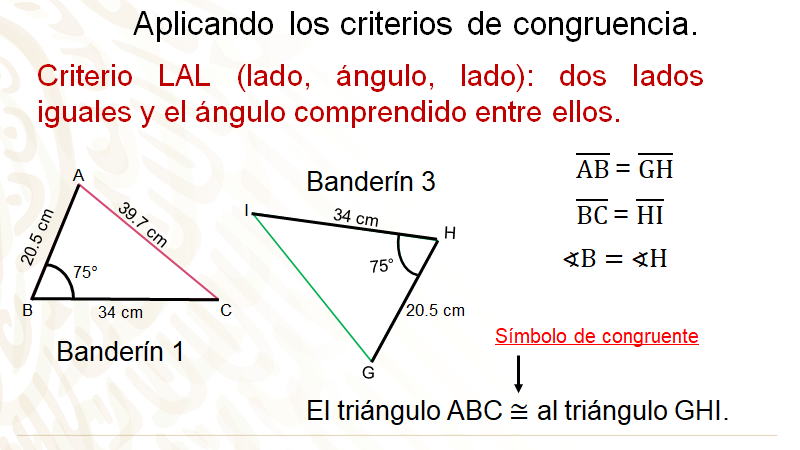
En el primer triángulo, inicia con el segmento AB y el segmento GH del segundo triángulo; puedes observar que ambos miden lo mismo 20.5 cm, por lo que estos lados son iguales.

Lo mismo se realiza con el segmento BC del primer triángulo; ¿con cuál segmento del banderín 3 es el correspondiente este lado?

El segmento HI es el correspondiente al segmento BC y, como puedes ver, ambos segmentos miden 34 cm, por lo que estos segmentos son congruentes.

Como puedes observar, el banderín el ángulo B está comprendido entre los lados AB y AC y su correspondiente, en el banderín 3, es el ángulo H y ambos miden 75 grados; por lo que el banderín de Sofía, el 1, y él de Ana, el 3, son triángulos congruentes, y lo estableces por el criterio de congruencia lado, ángulo, lado.

Utilizando los criterios de congruencia, puedes determinar que los triángulos 1 y 3; es decir, los banderines que realizaron Sofía y Ana, son congruentes: a diferencia del que hizo Fernando, ya que éste no cumplió con los criterios de congruencia y, al no ser congruente con el 1, tampoco lo es del 3.

¿El banderín de José, el número 4, será congruente con los banderines que realizaron Ana y Sofía? Para saberlo, aplica los criterios de congruencia.

Observa la siguiente imagen de los banderines 1 y 4, ¿qué criterio de congruencia puedes utilizar? Puedes utilizar dos criterios: lado, lado, lado y lado, ángulo, lado. En este caso, aplica el segundo criterio, ya que ambos triángulos cuentan con el dato de un ángulo.

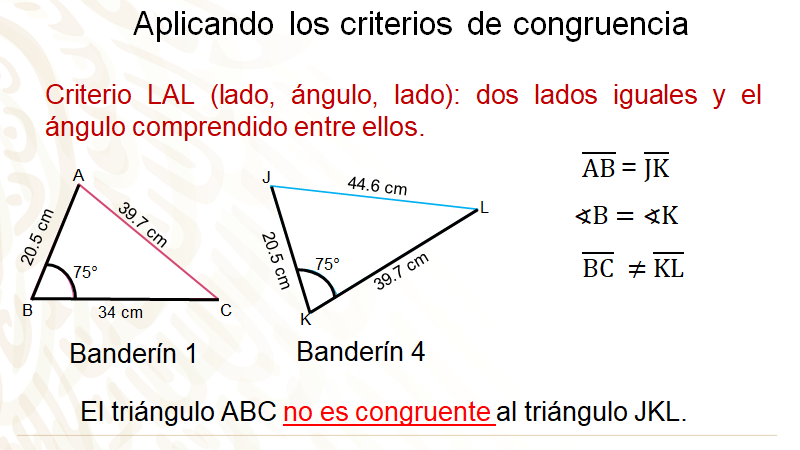
En el primer triángulo, inicia con el segmento AB y el segmento KL del cuarto triángulo, puedes observar que ambos miden lo mismo: 20.5 cm; por lo que estos lados son congruentes.

Entre estos dos lados AB y BC del banderín 1, se encuentra un ángulo B y su correspondiente es el ángulo K, comprendido entre los lados JK y KL. En ambos triángulos, el ángulo mide 75 grados.

Realiza la comparación del segmento BC del primer triángulo. ¿Con cuál segmento del banderín 4 se tiene que comparar, para saber si son congruentes? Su correspondiente es el segmento KL, que mide 39.7 cm, mientras que el segmento BC mide 34 cm; por lo que estos lados no son iguales.

Así que el banderín que hizo José no es congruente con el que hizo Sofía, ya que los triángulos no cumplen con el criterio de congruencia lado, ángulo, lado.

Al utilizar los criterios de congruencia, pudiste determinar que los banderines de Ana y Sofía fueron congruentes, a diferencia de los banderines de José y Fernando.

Observa los banderines y responde. ¿El banderín de Fernando, el 2, será congruente con el banderín de José, el 4? ¿Qué criterio de congruencia permite determinarlo?

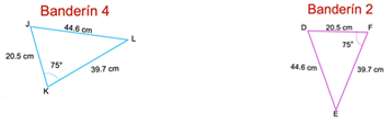
Si respondiste que son congruentes, estás en lo correcto, ya que cumplen con el criterio lado, lado, lado. Por lo que se puede decir que los banderines que realizaron Ana y Sofía son congruentes y los banderines que hicieron Fernando y José también lo son.

Revisa la siguiente situación, pon mucha atención y toma nota de la información más relevante para resolver las situaciones planteadas.

Javier, Carlos y Toño tienen que realizar una maqueta sobre una torre de alta tensión, para su proyecto de la asignatura de tecnología y Luis les ayudará a construirla. Cada uno de ellos realizó 10 triángulos; es decir, en total fueron 30 triángulos para hacer la torre.

Javier, Carlos y Toño le enviaron a otro compañero, Luis, los triángulos; él comenzará con la construcción de la torre de alta tensión. Luis inició comparando los diferentes triángulos que le enviaron sus compañeros para determinar si todos los triángulos eran iguales y, así, poder ensamblarlos con mayor facilidad.

Se te sugiere que analices la información para resolver las situaciones planteadas.

En la siguiente imagen se presentan los triángulos que realizaron cada uno de los alumnos, para el desarrollo de su proyecto. El triángulo 1 lo realizó Javier, el triángulo ABC; el segundo, lo realizó Carlos, el triángulo DEF; y el último triángulo lo realizó Toño, el KLJ.

¿Podrías establecer, a simple vista, si los triángulos son congruentes? ¿Qué medidas tomarías para determinarlo?

Considera las medidas de los lados; es decir, el criterio LLL, para hacer la comparación de los triángulos.

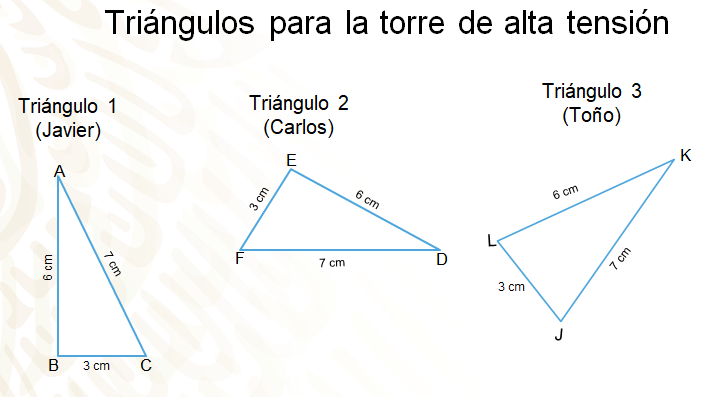
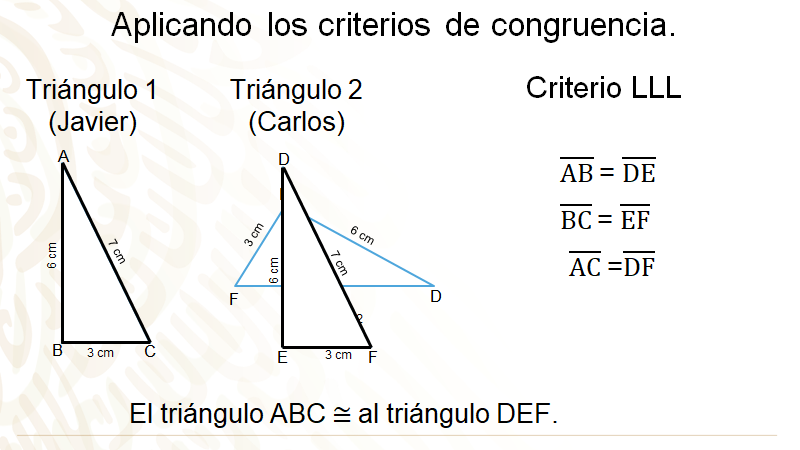
Inicia con los triángulos 1 y 2 que realizaron Javier y Carlos. Para tener un mejor panorama, gira el triángulo de Carlos hacia la derecha, para que quede en la misma posición que el de Javier. Analiza los lados de los dos triángulos. En el primer triangulo, compara el segmento AB con el segmento DE del segundo triángulo, puedes observar que ambos miden lo mismo, 6 cm, por lo que estos lados son iguales.

Realiza lo mismo con el segundo lado de ambos triángulos, del primero es el segmento BC, del segundo es el segmento EF. Puedes observar que ambos miden lo mismo 3 cm, por lo que estos lados también son iguales.

Por último, analiza el tercer lado de ambos triángulos, del primero es el segmento AC que mide 7 cm con el segmento del segundo triángulo, DF, que mide 7 cm; cómo puedes observar, estos lados son iguales. Por lo que se puede determinar que el triángulo ABC y el triángulo DEF son iguales; es decir, son congruentes.

Como verás Javier y Carlos realzaron triángulos congruentes.

Analiza el triángulo que realizó Carlos con el de Toño para verificar si también son congruentes.

Compara el segmento DF con el segmento JL. Puedes observar, en la imagen, que ambos miden 7 cm; por lo que estos lados son iguales.

Realiza lo mismo con el segmento EF del triángulo dos, ¿con cuál segmento del triángulo que realizó Toño se comparará para saber si son congruentes?

Con el segmento KL y ambos miden 3 cm.

Por último, analiza el tercer lado de ambos triángulos el segmento DE que mide 6 cm con el segmento del cuarto triángulo JK que mide 6 cm. Como se puede observar, estos lados son iguales. Por lo que se determina que el triángulo DEF y el triángulo JKL son congruentes.

Con esto, Luis ya sabe que los triángulos son congruentes y podrá armar, de manera más sencilla, la torre de alta tensión para poder entregar a tiempo el proyecto de la asignatura de tecnología.

Ahora se te invita a resolver el siguiente problema.

Don Julio es un herrero y tiene como trabajo construir una pieza en forma triangular, que se utilizará como base para detallar una escalera. Don Julio no pudo asistir a obtener las medidas y mandó a su ayudante, Pablo; pero se sintió inseguro al tomar las medidas de la pieza solicitada.

Pablo hizo tres posibles bocetos que le presentó a don Julio.

Observa el trabajo que hizo. Se te sugiere tomar nota de la información de la situación planteada.

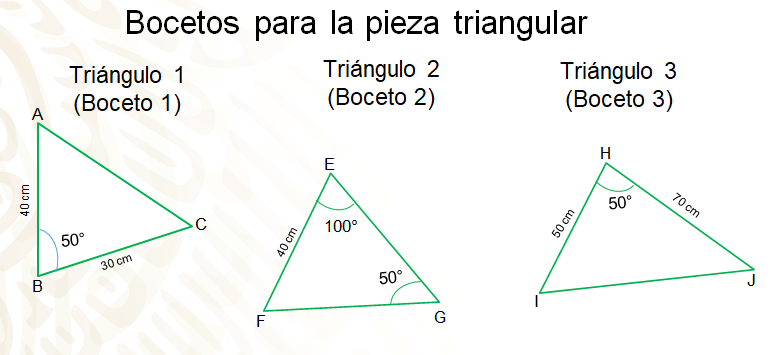
En la siguiente imagen se presentan los 3 triángulos que realizó el ayudante de don Julio; los triángulos 1, 2 y 3.

En cada uno, sólo consideró algunas de sus medidas para trazarlos. En el triángulo 1, el segmento BC mide 30 cm, el lado AB, que es del lado izquierdo, mide 40 cm y el ángulo B mide 50 grados. En el segundo triángulo, el segmento EF mide 40 cm, su ángulo G mide 50 grados y el ángulo E mide 100 grados. En el tercer triángulo, su lado HI mide 50 cm, su lado HJ mide 70 cm y el ángulo H mide 50 grados.

Con estos datos, ¿puedes establecer si los triángulos que trazó Pablo son congruentes entre sí?

Al tener dudas, don Julio le pidió a su ayudante que le diera todas las medidas que tomó y las anotó sobre un triángulo que trazó, sin medir.

Las medidas son las siguientes: el segmento KL mide 40 cm; el segmento LM, 30 cm; el tercer lado, KM 50 cm; el ángulo L mide 30 grados, el ángulo K mide 100 grados y por último el ángulo M mide 50 grados.

¿Cuál de los bocetos que realizó el ayudante de don Julio será congruente con el que se muestra?

Ahora se determinará cuál de los tres triángulos que realizó el ayudante de don Julio, es congruente con el que él realizó; y así, saber cuál de los tres bocetos es el correcto.

De acuerdo con los datos que tiene el primer boceto y los datos que tiene el triángulo que trazó don Julio, ¿qué criterio de congruencia puedes aplicar?

El criterio LAL (lado, ángulo, lado) es el que ayudará a hacer la comparación, ya que en los dos triángulos se conoce los valores de dos lados y el ángulo entre ellos, por lo que se puede aplicar este criterio.

¿Con qué medidas de los triángulos 1 y 4 iniciaras la comparación para verificar que sean congruentes?

Como conoces el ángulo B que mide 50 grados y el ángulo M que mide, también, 50 grados. Tienes que comparar los lados de ese ángulo para aplicar correctamente el criterio lado, ángulo, lado. Puedes considerar los lados BC y LM como correspondientes.

Entonces tienes que BC es igual a LM porque ambos segmentos miden 30 cm. Ya sabes que los ángulos B y M miden lo mismo, ahora sólo falta comparar el tercer dato del criterio elegido; en este caso son los segmentos AB y KM, que, como puedes observar, no son iguales, ya que uno mide 40 cm y el otro 50 cm. Por lo tanto, el triángulo ABC no es congruente con el triángulo KLM.

El primer boceto que hizo el ayudante de don Julio no cumple con las dimensiones del triángulo que necesita detallar para la escalera. Verifica el segundo boceto.

De acuerdo con los datos que tiene el segundo boceto y los datos que tomó don Julio, ¿qué criterio de congruencia se puede aplicar?

Para este caso, se usará el criterio ALA (ángulo, lado, ángulo), ya que en los dos triángulos se conoce los valores de dos ángulos y entre ellos está un lado comprendido; por lo que puedes aplicar este criterio.

¿Ya identificaste si los triángulos son congruentes? ¿Con qué ángulo del triángulo 2 y 4 iniciarías comparando para verificar que sean congruentes?

Se hará con el ángulo E del triángulo 2 y el ángulo K del triángulo 4, como puedes observar ambos ángulos miden 100 grados, por lo tanto, son iguales.

Realiza lo mismo con el ángulo L del cuarto triángulo; en este caso, ¿con qué ángulo del triángulo 2 se compararía para saber si son congruentes?

Con el ángulo F, pero no se conoce el valor de este ángulo. Y no puedes considerar los ángulos G y M, porque en el boceto 2 no está la medida del lado entre los ángulos E y G.

¿Cómo podrías encontrar la medida del ángulo F?

Se realizará por medio una ecuación de primer grado, ya que sabes que la suma de los ángulos interiores de los triángulos es de 180 grados y conoces la medida de los ángulos E y G.

Al sustituir, se realiza la suma de 100 grados + 50 grados + el ángulo F, dicha suma debe ser igual a 180 grados. 100 grados + 50 grados es igual a 150 grados. Aplicas la propiedad uniforme de la igualdad y restas en ambos lados de la igualdad 150 grados; eso te da como resultado que el ángulo F es igual a 30 grados.

Ya puedes comparar estos ángulos, el ángulo L mide 30 grados lo mismo que el ángulo F, sólo falta comparar el lado EF con el lado KL y ambos miden 40 cm; por lo que el triángulo EFG es congruente con el triángulo KLM.

Don Julio ya sabe cuál es el boceto que realizó de manera correcta su ayudante, la pieza triangular que debe considerar es el triángulo 2 que hizo Pablo, su ayudante. El triángulo 3 ya no lo comparas, porque tiene un lado de 70 cm y no corresponde con ninguno de los lados del triángulo modelo.

Como observaste, los triángulos son utilizados en muchas situaciones cotidianas, como en la construcción, ya que es la única figura geométrica que no se deforma cuando se le aplica una fuerza.

Los criterios de congruencia en triángulos ayudan a verificar la relación entre diferentes triángulos conforme a sus elementos. No olvides que, para que dos triángulos sean congruentes, se debe cumplir al menos uno de los tres criterios de congruencia. El primero de ellos es el criterio lado, lado, lado; el segundo criterio lado, ángulo, lado; y el tercer criterio ángulo, lado, ángulo.

El reto del hoy:

Revisa en tu libro de texto el tema que estudiaste en esta sesión y realiza las actividades que ahí se sugieren.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html