Proporcionalidad inversa y arquitectura maya
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
Proporcionalidad inversa y arquitectura maya
Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: analizar y comparar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Hoy se construirá geométricamente la curva que describe una proporcionalidad inversa.
¿Qué hacemos?
Para iniciar la sesión, reflexiona, ¿a quién no le gusta visitar alguna zona arqueológica?
¡En verdad eres muy afortunado!, ya que en el país se cuenta con una gran variedad de ruinas como Teotihuacan, Monte Albán, Uxmal, Tulum, Tajín, por sólo mencionar algunas que hoy puedes disfrutar en su infinita belleza y en todas ellas impresionan sus grandes construcciones.
En esta sesión vas a estudiar el vínculo entre las matemáticas y, en particular, la arquitectura maya. Seguramente te preguntarás: ¿de verdad las matemáticas tienen alguna relación con los mayas?
Los mayas tenían conocimientos de astronomía, matemáticas y agricultura, por mencionar algunos. Pero desde la perspectiva de las matemáticas uno de sus principales logros fue la invención de una representación matemática del cero, así como estudios de astronomía y de arquitectura.

¡Vaya que sí debes sentirte orgulloso de tus raíces!
Ahora, hay que analizar un poco la arquitectura maya. ¿Sabías que la cascabel yucateco, la serpiente endémica del sureste de México y parte de Centroamérica, era considerada un animal sagrado?
En la piel de esta serpiente los mayas encontraron una figura en forma de rombo llamada canamayté, la cual inspiró diseños arquitectónicos.

Así, inspirados por el ingenio de los mayas, verás aplicaciones del concepto de proporcionalidad inversa en la construcción, y así mismo, una representación geométrica de ella.
Ahora, verás cómo dar sentido y significado a la geometría de una proporción inversa. Para ello revisa la siguiente situación.
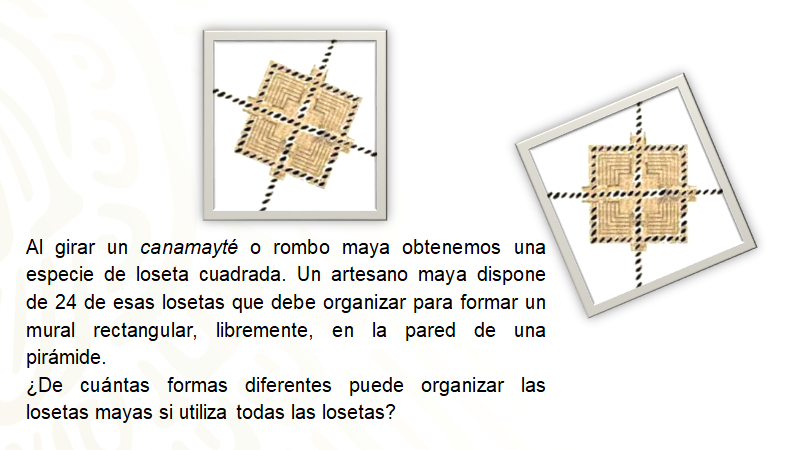
Como ya se tienen 24 losetas, una forma de organizar las losetas puede ser 4 columnas de 6 losetas de altura cada una.
Otras formas de acomodar pueden ser 8 columnas con 3 losetas de altura cada una, o una, que tal vez no es la más común, colocar todas las losetas una seguida de otra, lo cual daría un mural de 24 columnas con una loseta de altura cada una, lo cual daría un mosaico muy largo. Otro arreglo menos extenso serían 12 columnas con 2 losetas de altura cada una.
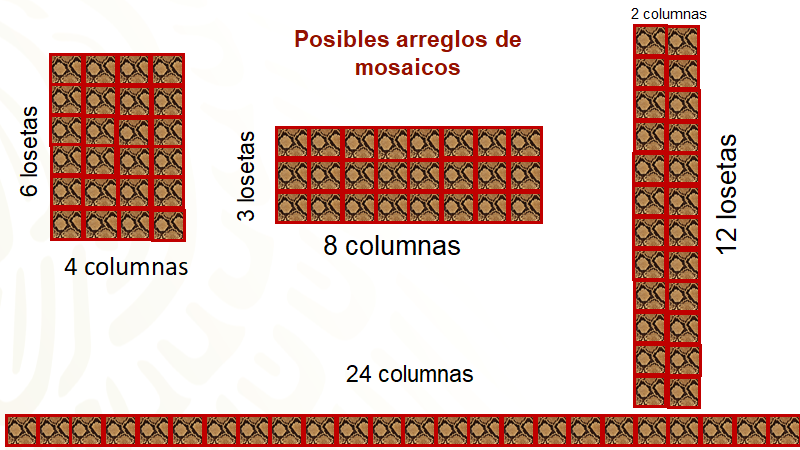
Las distintas formas de los mosaicos pueden tener un comportamiento entre las magnitudes de la base y altura de un rectángulo. Así es; si analizas en todos los posibles arreglos, hay algo que permanece constante, el número de las losetas que son 24, la superficie o área que abarca cada mural es la misma, por lo cual se observa que cuando el número de columnas aumenta, el número de losetas por columna disminuye en la misma proporción, es decir, dichas magnitudes están en proporción inversa.
Ya que se están construyendo mosaicos mayas que son agradables visualmente, observa que una proporción inversa no se queda atrás. Se te invita a que analices visualmente una proporción inversa, pues has trabajado tablas donde se ordenan los datos.
En este caso se hace un análisis del concepto de una proporción inversa utilizando aritmética, pero en las matemáticas existen distintas ramas, entre ellas, la geometría, por ejemplo, que ayudan a desarrollar un concepto desde otra perspectiva. Observa como:
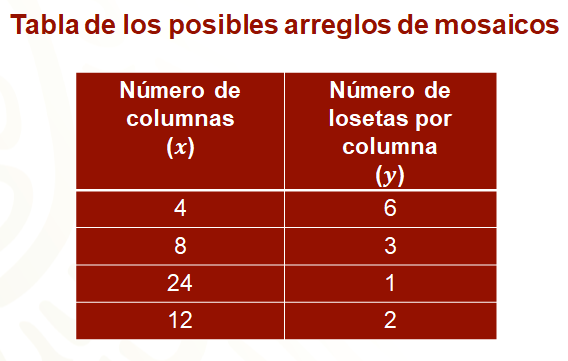
Para ello se realiza un arreglo tabular donde en la primera columna se coloca el número “x” de columnas que forman el mosaico y en la segunda columna el número “y” de losetas en cada columna.
Así, a partir de la propuesta inicial, en el primer renglón de la tabla se colocan 4 columnas con 6 losetas cada columna; en una segunda propuesta se tienen 8 columnas con 3 losetas cada una; en el tercer mosaico demasiado largo que corresponde al tercer renglón de la tabla se tienen 24 columnas con una loseta en cada columna, y en el último renglón, un mosaico con 12 columnas y 2 mosaicos por cada una.
Asimismo, se corrobora que se está en una proporción inversa, comparando los datos en el primer y último renglón, ahí se nota que mientras el número de columnas se triplica, el número de losetas por columna disminuye a la tercera parte, y de manera análoga con el segundo y tercer renglón.
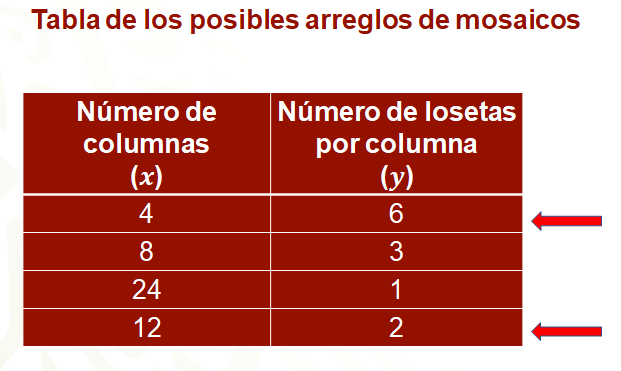
Ahora, se hará uso de los datos en la tabla para el análisis geométrico de una proporción inversa, de, su arquitectura.
Se van a trazar dos segmentos de rectas perpendiculares entre sí, que llaman ejes de coordenadas, obteniendo así un eje horizontal donde se ubicará la variable “x”, que es el total de columnas en cada mosaico, es decir, los datos de la primera columna de la tabla, mientras que en el eje vertical se ubica la variable “y”, que representa el número de losetas en cada columna del mosaico correspondiente, que son los datos de la segunda columna de la tabla. Para simplificar la representación es conveniente elegir una escala en cada uno de los ejes, de donde por la forma que se encuentran representados los datos, se puede elegir una escala de 4 en 4 para ir haciendo marcas a la misma distancia en el eje horizontal y, por otro lado, la escala será de 2 en 2 para el eje vertical.
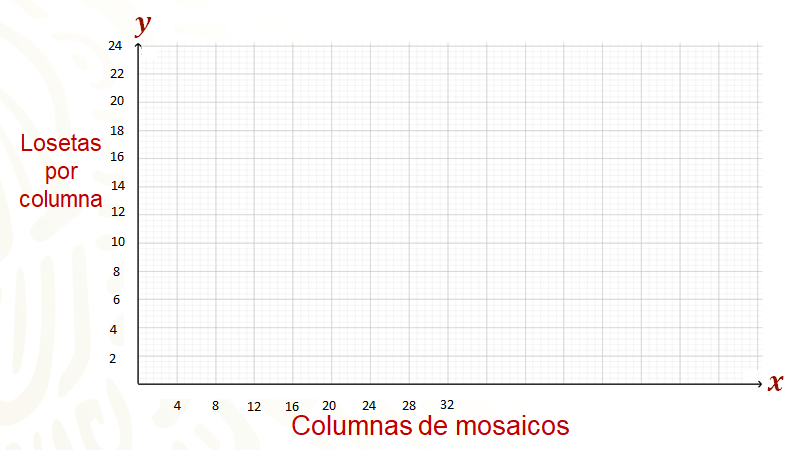
Con los datos del primer renglón se tiene que “x” es igual a 4 y “y” es igual a 6, formando la pareja ordenada “cuatro coma seis”; trazando rectas paralelas a los ejes por los puntos marcados en los ejes, se busca su punto de intersección identificando dicho punto “P” con la pareja formada.
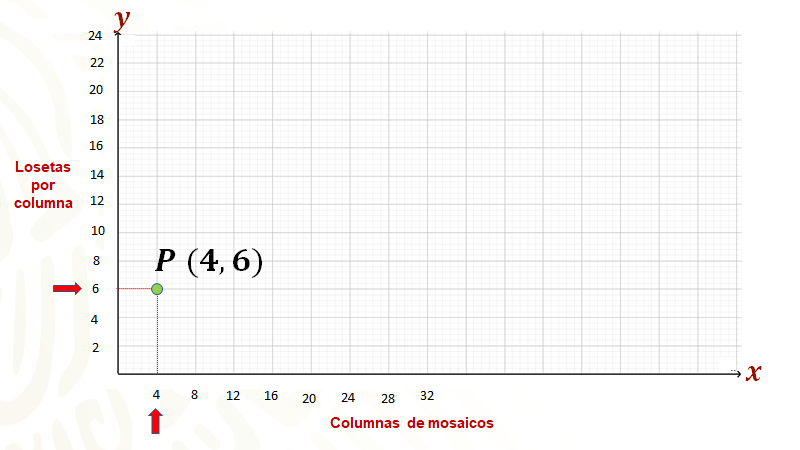
Se procede de la misma manera con el resto de los datos en la tabla, para así ir ubicando puntos que van formando una representación geométrica de la proporción inversa de la tabla que se construyó.
Ahora se localiza primero el “8” en el eje horizontal, que por la escala se ubica en la segunda marca, de la misma manera, pero en el eje vertical se ubica “3” que por la escala se encuentra a la mitad de entre la segunda y tercera marca del eje donde se está trabajando; con ello, se forma la pareja “8 coma 3”. Ahora se trazan rectas paralelas a los ejes para encontrar su punto de intersección, al cual se le llamará el punto “Q”.
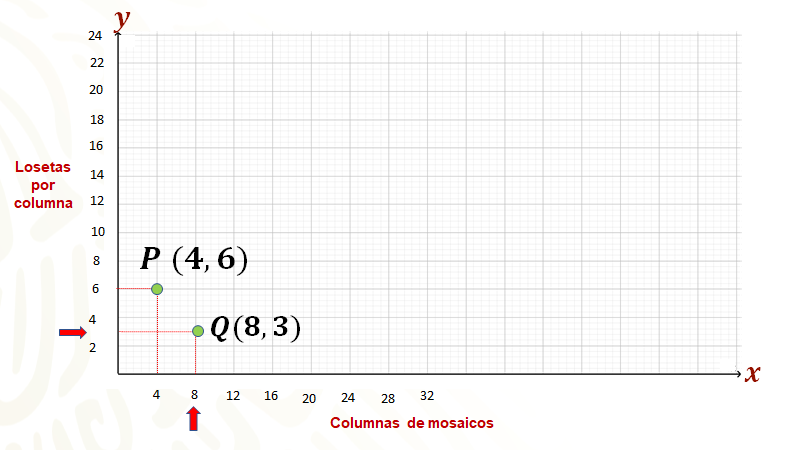
Procediendo de manera análoga, se ubica el resto de los puntos, a los cuales se les llamará “R” y “S” en los ejes de coordenadas. Si observas, hay puntos que están más arriba del eje horizontal que otros, inclusive hay un hueco entre el punto “R” y “S”; lo que puedes hacer es calcular más puntos en la tabla dando valores a “x”, determinando el valor faltante en la proporción inversa, y procediendo después a formar las parejas ordenadas correspondientes para ubicarlas en el plano. Observa.
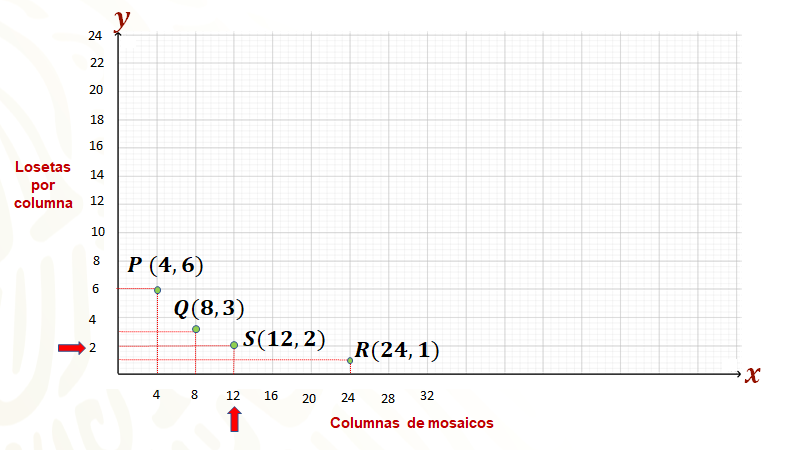
Para ello, se van a dar los valores de 16 y 18 para “x” en la primera columna para obtener el valor correspondiente de “y” en la segunda columna.
Así, para el valor de “x” igual a 16, que es el doble de 8; en la segunda columna se tiene que el valor de “y” correspondiente es la mitad de “3” es decir, tres medios o 1.5, con lo cual se tiene el punto “T”, con coordenadas “16 coma tres medios”, que bajo las condiciones del problema, corresponde a un mosaico con 16 columnas cada una con una y media loseta de altura.
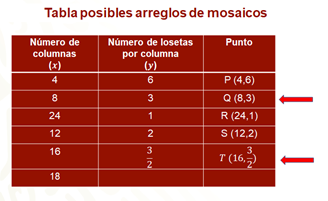
Para el valor de “x” igual a 18 se observa que el procedimiento puede complejizarse respecto al anterior, pero puedes recordar la propiedad que cumplen las variables de una proporción inversa, donde los productos de las magnitudes en cada renglón son constantes para tener que, 18 por “y”, es igual a 4 por 6.
De donde 18 por “y” es igual a 24, dividiendo de ambos lados en la igualdad anterior por 18, se tiene que “y” es igual a 24 sobre 18.
Simplificando la fracción, se tiene que “y” es cuatro tercios o un entero un tercio. Para tener el punto con coordenadas “U”, 18 coma cuatro tercios o un entero un tercio, y se coloca en la tabla.

Ahora, representando los nuevos puntos en la gráfica, se tiene que. puedes visualizar la representación geométrica de una proporción inversa, se ve cómo los puntos van bajando al eje horizontal.
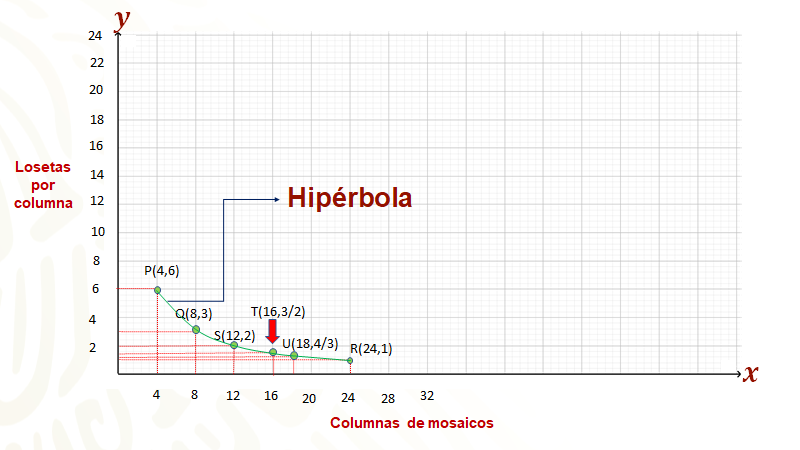
Inclusive si vas considerando cada vez más valores para “x” de manera continua, sin dejar huecos, se van obteniendo más y más puntos que satisfacen las condiciones del problema, que, al ubicarse en el plano, se va observando el trazo de una curva continua que va uniendo todos los puntos, llamada hipérbola, que va a ser la representación geométrica de la proporción inversa.
La cual, por cierto, modela el fenómeno de una curva que va bajando hacia el eje horizontal conforme se va alejando del punto de intersección de los ejes que es el origen, cuyas coordenadas son “cero, coma cero”.
Ahora, se te invita a que reflexiones sobre la siguiente pregunta: ¿qué pasa conforme se acercas al cero?
Para responder la pregunta, se va a considerar una tabla ahora con valores de "x" próximos a cero, a partir del primer renglón que corresponde a un mosaico de 4 columnas con 6 losetas cada una, y recordando que en una proporción inversa, conforme una variable disminuye, la otra aumenta en la misma proporción, se tiene que, para cuando “x” vale 2, es decir, la mitad de 4, entonces el valor de “y” es el doble de 6, que es 12, por ello, en el penúltimo renglón se tiene el punto “(2,12)”; siguiendo con esa idea, para el siguiente renglón la mitad de 2 es ahora 1, que es el nuevo valor para “x”, y así sucesivamente se obtienen valores de “x” cercanos a “cero”, calculando las mitades del renglón inmediato anterior obteniendo así un medio, que es la mitad de 1, y un cuarto que es la mitad de un medio en la primera columna, por estar en proporción inversa con “y” se puede completar la segunda columna obteniendo el doble del valor en el renglón inmediato anterior, con lo cual, el doble de 12 es 24 y así sucesivamente.
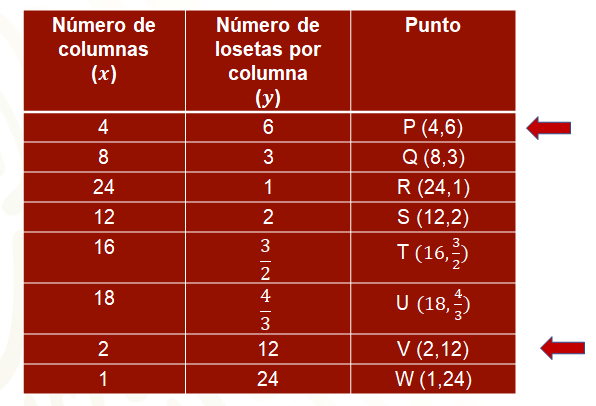
Ahora, formando las parejas correspondientes se obtienen los puntos de la tercera columna. que al representarlos en el plano con ejes de coordenadas, junto con el resto de los puntos, se tiene la siguiente configuración de puntos, que al unirlos con una curva continua, se obtiene una mejor idea de la hipérbola que representa la proporción de los mosaicos mayas, donde puedes observar que, conforme te aproximas a cero con valores en el eje horizontal tanto como quieras, con los valores de “y” te vas aproximando más y más al eje vertical, además de crecer la curva tanto como sea necesario.
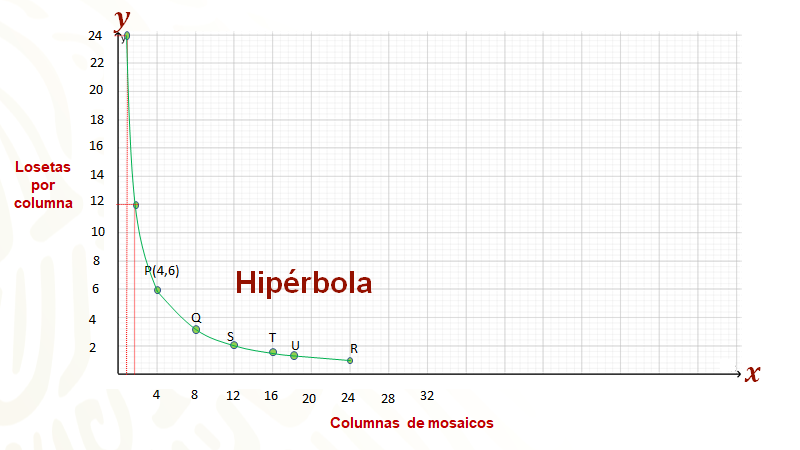
Es momento de hacer un alto en el desarrollo del tema, para puntualizar lo estudiado hasta aquí. Se verán los pasos para trazar la gráfica que representa una proporción inversa.

Ahora, se revisará una última situación.
Actualmente, con la construcción de un tren en el sureste del país, se busca tender un drenaje entre dos zonas arqueológicas mayas, se necesitan 6 000 tubos de 2.40 metros de largo.
Hay que determinar una manera gráfica de la relación existente entre el número de tubos “T” y la longitud “L” de cada uno de ellos.

Observa que conforme los tubos aumentan de tamaño, el número de tubos van a disminuir en la misma proporción, ya que la distancia entre ambas zonas arqueológicas no va a cambiar, por lo que se trata de graficar una proporción inversa entre las variables “T” y “L”.
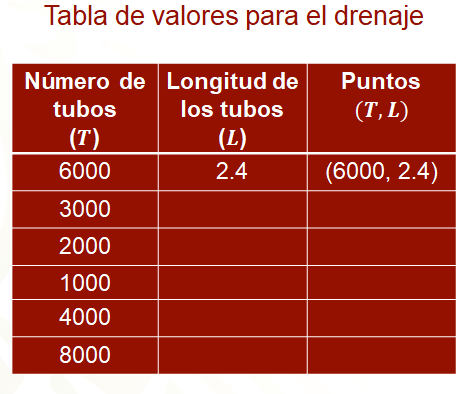
Hay que considerar una tabla donde se encuentran tres columnas una para el número de tubos en la obra “T”, una segunda columna para la longitud correspondiente del tubo “L” y una última para ir formando las parejas ordenadas que pueden ayudarán a trazar la gráfica.
En el primer renglón se colocan 6 000 tubos a los que les corresponde 2.4 metros en la segunda columna, formando la pareja (6 000, 2.4).
Ahora, se proponen los demás valores para que sea accesible graficar; por ejemplo, se consideraron los siguientes valores de “T” en la primera columna: “3 000” tubos la mitad de “6 000”, “2 000” tubos la tercera parte de “6 000”, ”1 000” tubos la sexta parte de “6000”, “4 000” el doble de “2 000” y así hasta “8 000”, que es el doble de “4 000”; en la segunda columna se colocan las longitudes “L” correspondientes de los tubos para luego escribir en la última columna los puntos.
Para calcular las longitudes de los tubos, como las variables están en proporción inversa, entonces disminuyen y aumentan en la misma proporción; así, los datos para completar la tabla se obtienen usando esa condición, así, se tiene que en el segundo renglón el valor de “L” es 4.8, que es el doble de 2.4; para el tercer renglón, su valor es 7.2, que es el triple de 2.4; en el cuarto renglón, 14.4, que es el doble de 7.2; en el quinto renglón es 3.6, que es la mitad de 7.2; en el sexto renglón es 1.8, que es la mitad de 3.6.
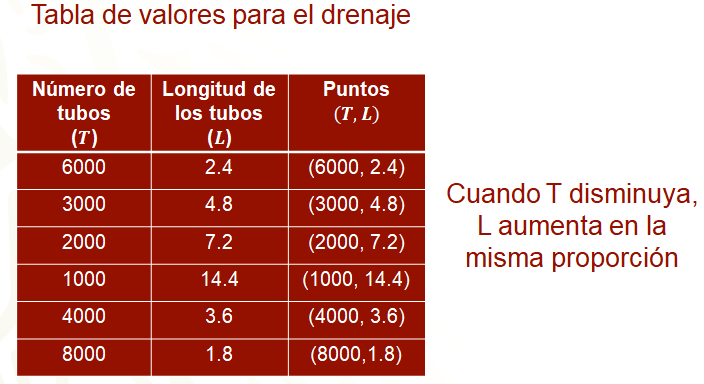
Como te diste cuenta, completar los datos de la tabla sabiendo que las variables están en proporción inversa fue relativamente fácil. Se precisa, que en una relación de proporcionalidad inversa la disminución de una cantidad implica el aumento de la otra, siempre en la misma proporción.
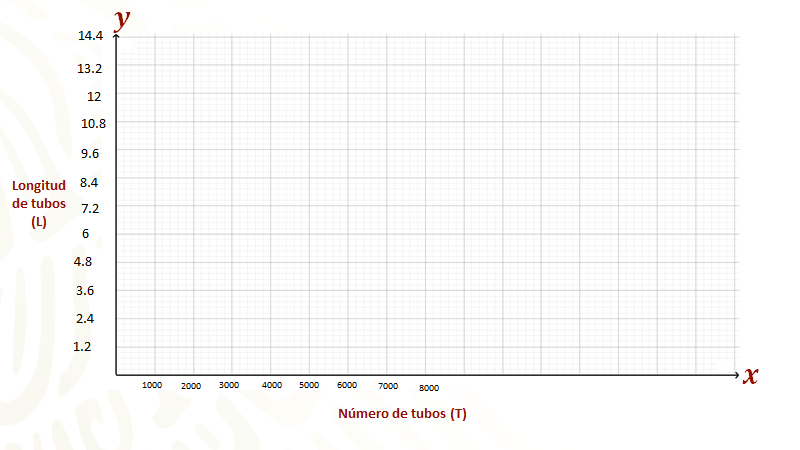
Ahora, se procede a realizar la gráfica ubicando primero las variables sobre los ejes de coordenadas, en el eje horizontal se ubica la variable “T” de la primera columna y en el eje vertical, la variable “L” de la segunda columna.
Después se procede a ubicar los puntos de la tercera columna, recordando que hay que buscar la intersección de las rectas paralelas a los ejes. Resultando un arreglo de los puntos como el que se puede ver en la siguiente gráfica.
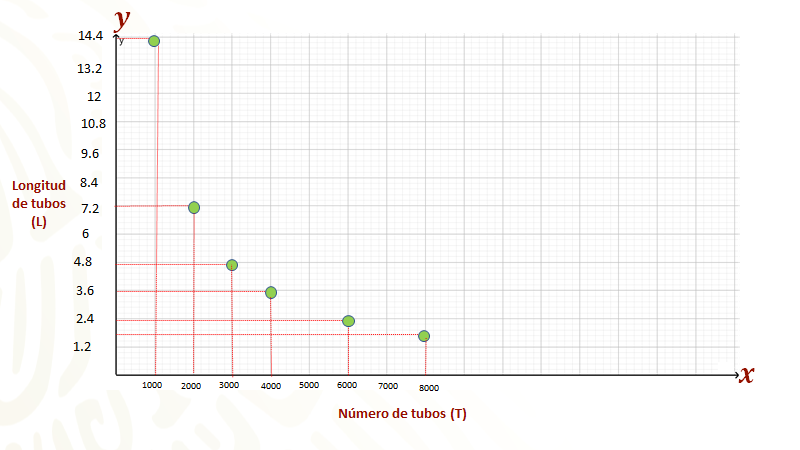
Al final se unen los puntos con una curva continua, para finalmente obtener la curva que representa la relación entre las variables “T” y “L” que son inversamente proporcionales.
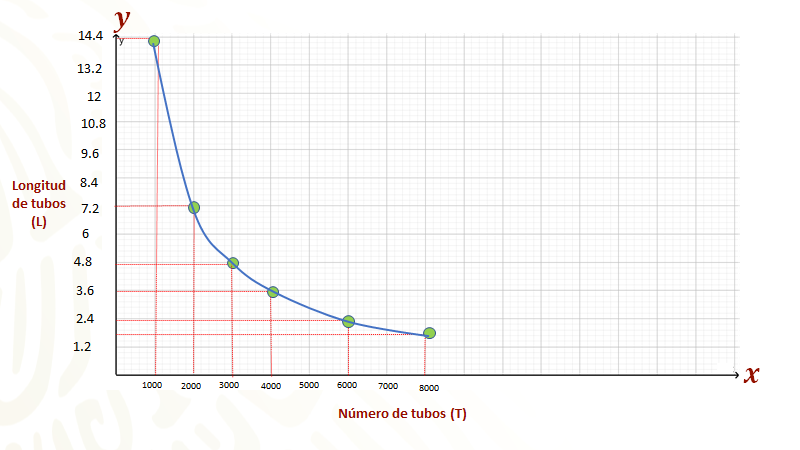
Se espera que hayas dado sentido y significado a la representación geométrica de la proporcionalidad inversa.
Una consideración que se tiene que tomar en cuenta es que al igual que en la proporcionalidad directa, en los casos de proporcionalidad inversa también se puede hallar una constante que te ayude a calcular algún valor faltante, ya sea de “x” o de “y”.
En este caso se llama constante de proporcionalidad inversa, ya que las variables son inversamente proporcionales, y se puede calcular de la siguiente manera.
Se van a utilizar los datos de las losetas mayas, que es una situación que ya se resolvió al inicio de la sesión.
En la situación se contaba con 24 losetas y se plantearon las siguientes maneras de agruparlas:
- 24 columnas por 1 loseta de alto.
- 12 columnas por 2 losetas de alto.
- 8 columnas por 3 losetas de alto.
- 4 columnas por 6 losetas de alto.
Primero se llamará “x” a los valores correspondientes a las columnas y “y” a los valores que correspondan al alto de losetas.
Si analizas los datos puedes percatarte de que el producto de “x” con su correspondiente valor de “y” es siempre el mismo, 24. Este valor representa la constante de proporcionalidad inversa y se llamará “k”, y puede ayudarte a calcular el número de columnas si conoces el número de losetas y viceversa.
La fórmula que relaciona a la constante de proporcionalidad inversa con las variables, tanto independiente como dependiente, es la siguiente: “x” por “y” igual a “k” o “y" es igual a "k" entre "x”, lo cual es la representación algebraica de una proporción inversa.
Para esta situación y con esta expresión algebraica es posible calcular cualquier combinación de losetas que se requiera, siempre y cuando no sean mayores a 24, por el planteamiento del problema, aunque observa que la expresión algebraica puede ya extenderse a otros valores, dejando de depender del problema y poder ya tener independencia para su estudio más adelante.
Has concluido el tema del día de hoy. Se te recuerda que debes elaborar tus notas, considerando las ideas más importantes del tema de hoy, anota tus dudas y posibles dificultades, para que de ser posible las puedas revisar con tu profesora o profesor de esta asignatura.
El reto de hoy:
Te proponemos el siguiente reto:
Dadas dos magnitudes “x” y “y” que son inversamente proporcionales con constante de proporcionalidad negativa “k” igual a menos uno. Se te invita a realizar una tabla donde se calculen distintos valores de “x” y “y” que satisfagan dicha proporción, y que elabores la representación gráfica de la proporción a partir de las parejas de puntos en el paso anterior en el plano cartesiano.
Finalmente, describe el comportamiento de la curva analizando la variación de “y” respecto a la variación de “x” para valores próximos y lejanos al cero.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion