Situaciones de variación lineal
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42
Situaciones de variación lineal
Aprendizaje esperado: analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación.
Énfasis: relacionar las representaciones tabulares, gráfica y algebraica de situaciones de variación lineal: y = ax + b.
¿Qué vamos a aprender?
En esta sesión ampliarás tus conocimientos sobre el aprendizaje esperado: “Analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación”.
¿Qué hacemos?
Comenzarás con un juego lógico-matemático llamado el “Salto de la rana”, basado en el intercambio de posición de tres fichas azules y tres fichas rojas colocadas como se muestra a continuación.

Como puedes observar, se encuentra un espacio vacío para colocar una ficha más; este espacio servirá para ir moviendo las fichas considerando las siguientes reglas:
- Se puede mover sólo una ficha a la vez.
- Únicamente puedes saltar como máximo una ficha, no más.
- Las fichas azules deberán quedar en el lugar en que se encuentran las fichas rojas y las rojas en el lugar que se encuentran las azules.
- Las fichas se deben mover únicamente en dirección adonde quedarán al final del juego y no pueden retroceder una vez movidas.
- Si lo intentas y ya no pueden mover más fichas, siguiendo las reglas establecidas, deberás colocar nuevamente las fichas como en un inicio y volver a comenzar.
Considera que las fichas las puedes elaborar con material reciclado, usar los colores que te gusten u otros. Al final de esta sesión, verás alguna pista que seguramente ya habrás deducido al jugar el “Salto de la rana”.
Al estudiar algunas situaciones cotidianas, se pueden usar literales para representar cantidades denominadas constantes, es decir, que su valor permanece fijo y son representadas convencionalmente por las letras ("a", "b", "c"). y otras conocidas como variables, aquellas que pueden adquirir o tomar distintos valores, representadas regularmente con las letras ("x", "y", "z"), aunque es posible utilizar cualquier literal.
Las variables pueden ser dependientes o independientes. Las variables independientes son aquellas que pueden adquirir o se les puede asignar cualquier valor. Las variables dependientes son aquellas cuyos valores dependen de los valores que adquieran o que se les asignen a las variables independientes.
Considera expresiones algebraicas que están formadas por los dos tipos de variables y por valores constantes. Comienza identificando en un problema cotidiano los valores constantes y variables inmersos en él.
En cierta localidad, el kilogramo de tortilla cuesta 15.00 pesos y llevan una servilleta o manta de tela para no pagar un costo extra por el papel en el momento que les entregan las tortillas.
Inicia por identificar el valor constante. ¿Lo tienes?
En este caso la constante son quince pesos por kilogramo.
Ahora, ¿cuáles son las variables en caso de comprar más o menos en cantidad de tortillas de la unidad establecida, es decir, de un kilogramo?
La cantidad de kilogramos que vayas a comprar puede ser menor, igual o mayor a un kilogramo. El costo a pagar depende de la cantidad de tortillas que se compren. Con base en la identificación realizada, se puede establecer que se tiene una expresión algebraica del tipo.
y = ax, en donde:
"a" representa el costo por kilogramos de tortilla;
"x", la cantidad de kilogramos de tortillas a comprar; y
"y", el costo total a pagar.
Si cambias la constante “a” por el valor establecido del kilogramo de tortilla, tienes la expresión algebraica y = 15x.
Elabora una tabla a partir de medio kilogramo de tortillas hasta 5 kg.

Para ello, al multiplicar los valores de equis por 15 se obtiene el correspondiente valor de "y". Así se tiene que por medio kilogramo se pagan 7.50 pesos; por un kilogramo, 15 pesos; por 2, 30 pesos; por 3, 45 pesos; por 4, 60 pesos y por 5, 75 pesos.
Al graficar estos valores considera en el eje de las "x" los kilogramos de tortillas, y en el eje de las "y", el costo a pagar. Se ubican los puntos coordenados (x, y) y se traza la recta que se genera con todos los puntos que forman parte de la expresión algebraica.
Observa con atención cómo a cada valor en la coordenada “x” corresponde otro en “y”; es diferente para cada valor. Al unir los puntos se forma una línea recta, misma que indica un crecimiento. Es decir, conforme aumenta el peso, aumenta el costo a pagar. Así identificas que el peso es la variable independiente, mientras que el costo a pagar es la variable dependiente.
Ahora supón que el dueño de la tortillería quiere innovar, por lo que decide elaborar tortillas de menor tamaño para las taquerías cercanas a su negocio. Pero al ser de un tamaño especial, el costo varía, en este caso es de 18.50 pesos por kilogramo y únicamente venderá kilogramos completos. Será necesario elaborar una nueva tabla para registrar la información. En este caso, ¿qué expresión algebraica corresponde a esta nueva situación?
Identifica el valor constante. Para este caso será el costo por kilogramos de la tortilla para tacos, es decir, 18.50 pesos, mientras la variable independiente “x” será la cantidad de tortillas por comprar y la variable dependiente “y”, el costo total de la compra.

La expresión algebraica quedaría establecida de la siguiente manera.
y = 18.5x.
Completa la tabla correspondiente.
Al graficar la expresión algebraica, considera que en el eje de las "x" los kilogramos de tortillas y en el eje de las "y" el costo a pagar. Ubicamos los puntos coordenados (x, y) y se traza la recta que se genera con todos los puntos que forman parte de la expresión algebraica.
Para completar la tabla de datos correspondiente, sustituye a "x" por valores del 1 al 5 y los multiplicas por la constante 18.5 para obtener los valores correspondientes de "y". Así, se tiene que por un kilogramo se pagan 18.5 por uno, igual a 18.5; por 2 kilogramos, 18.5 por 2, igual a 37 pesos; por 3 kg, 55.50 pesos; por 4 kg, 74 pesos, y por 5 kg, 92.50 pesos.
Al graficar los datos considera en el eje de las "x" los kilogramos de tortillas y en el eje de las "y", el costo a pagar; ubica los puntos coordenados (x, y) y traza la recta que se genera con los puntos. Se te invita a revisar lo anterior en el siguiente audiovisual.
- Variación proporcional directa.
Ahora compara las rectas generadas por las dos situaciones consideradas.

Observa cómo el crecimiento de la expresión algebraica y = 18.5x es mayor que la expresión algebraica y = 15x. La diferencia está en la razón de cambio, en la segunda situación es mayor que la primera.
Ya observaste que la expresión algebraica y la recta graficada son dos herramientas matemáticas equivalentes, es decir, de una puedes obtener la otra y viceversa.
¿Será cierto? Lo descubrirás más adelante.
Para obtener la razón de cambio en una expresión algebraica lineal, es necesario observar la variación de cambio de “x” y “y” en intervalos iguales; es decir, de uno en uno, de dos en dos, etc.
A continuación, analiza y completa 3 tablas, las cuales muestran los tres distintos salarios diarios de una compañía en la que se manejan tres variantes, de acuerdo con las comisiones por ventas realizadas.
- Esquema "A": No hay sueldo base, pero sí una comisión que corresponde a la mitad de las ventas diarias.
- Esquema "B": Hay un sueldo base de 50 pesos diarios más una comisión de la quinta parte de sus ventas; es decir, 20 por ciento de sus ventas.
- Esquema "C": El sueldo base es de 150 pesos diarios; no hay comisión por ventas.
Analiza cada esquema y encuentra la expresión algebraica que establece la relación de cada tabla mostrada.

Estas expresiones algebraicas son de la forma y es igual a “ax + b”.
Comienza con el esquema “A”; ¿cuál es la constante “a”? La comisión que equivale a la mitad de las ventas diarias. El monto de la venta diaria es la variable independiente “x”, y “b” es igual a cero. Entonces “y” es igual a “ax”, es decir:
y = 1/2x, y = x/2 o bien y = 0.5x; estas tres son expresiones algebraicas equivalentes.
En la tabla del esquema A se establecen las ventas en pesos para 100, 200, 300, 500, y duplicando la última venta, hasta 1 000 pesos. Se completa la tabla multiplicando (1/2) por cada valor de “x”. Por ejemplo, (1/2) (100), multiplicando 100 por uno y dividiendo el producto entre 2; da como resultado 50.
Otra forma es convertir la fracción 1/2 a número decimal, que es (0.5) y multiplicarlo por 100; queda (100) (0.5) = 50; o bien para la expresión y = x/2, únicamente se divide el valor de las ventas entre 2. Les invito a completar la tabla del esquema "A", el cual debería quedar como se muestra.
Continuando con el esquema "B", se tiene sueldo base fijo de 50 pesos que es una constante, la constante “b”. La variable independiente nuevamente son las ventas realizadas durante el día, multiplicada por 1/5 de ellas, que será la comisión. Este dato, 1/5, también aparece como constante, la constante “a”.
Entonces “y” = “ax + b”, donde 1/5 sería la constante “a” y el sueldo base de 50 pesos sería la constante “b”. Así, la expresión algebraica queda como:
y = 1/5x + 50, y = x/5 + 50 o bien y = 0.2x + 50
Para completar la tabla, se multiplica (1/5) por cada valor establecido de “x”, por ejemplo (1/5) por (100), y al sumar el sueldo base de 50 pesos se obtiene como resultado 70 pesos.
Utilizando las otras expresiones equivalentes puedes dividir las ventas entre 5 y sumar 50 al resultado, o multiplicar las ventas por 0.2 y sumar 50 al resultado.
Con el procedimiento que hayas elegido, te invito a completar la tabla del esquema "B", la cual queda como se muestra.
Sigue con el esquema "C". Se tiene sueldo base fijo de 150 pesos, al no variar es una constante “b”, pues no tiene relación con la variable “x”. A diferencia de los esquemas "A" y "B", “y” no está expresada usando una variable independiente como “x” al no haber comisión relacionada con las ventas diarias. Únicamente se tiene el sueldo base de 150 pesos. Entonces, para el esquema "C", “y = 150”.
Para resolver no hace falta hacer ninguna operación porque, sin importar las ventas realizadas en el día, el sueldo fijo será siempre de 150 pesos.
Ahora grafica las tres rectas en un mismo plano cartesiano. De esta forma puedes comparar los comportamientos de los diferentes esquemas.

Si analizas gráficamente un sólo valor de la variable “x”, es decir, ventas diarias, y observas el valor correspondiente de “y”, podrías determinar para ese valor qué esquema de pago le convendría elegir. Por ejemplo: para una venta de 300 pesos en cada esquema, ¿cuál le convendría elegir a un empleado? Y si se analiza la venta máxima considerada en las tablas, es decir, 1 000 pesos, ¿debería el empleado cambiar de elección o quedarse con el mismo esquema?
Ahora se partirá de tres rectas en el plano cartesiano. Cada una representa el costo por servicio de taxis en distintas ciudades.

Se te invita a analizar por unos segundos las rectas que representan el comportamiento de cada expresión algebraica en relación con sus valores constantes y sus variables. Revisa los valores de “y” con respecto de “x” en el plano cartesiano considerando intervalos iguales para lograr una comparación equitativa.
Para continuar extrae los datos de cada una de ellas, elaborando una tabla por compañía.
Si observas con detenimiento, para cada recta en el plano cartesiano el costo en el primer kilómetro recorrido te servirá como dato inicial para cada una de las tablas, las cuales comenzarás a completar en el siguiente formato sugerido para cada una de ellas.
Observa primero la variación entre intervalos iguales en la tabla correspondiente a la gráfica de la compañía “A”. Por ejemplo, cuánto varía “y” cuando “x” incrementa de 1 en 1.

Para la primera comparación, “y” pasa de un valor de 11.50 a 15 pesos. Observa, la variación fue de 3.50 pesos.
Ahora observa la segunda variación, cuando a “x” se le asignan los valores de 2 y 3, “y” obtiene los valores de 15.00 a 18.50 pesos respectivamente, la variación de nuevo es de 3.50 pesos, lo que significa que permanece constante. Por lo tanto, podrías asegurar que cada valor que toma la variable “x” es multiplicado por 3.5 que es constante “a”.
Pero al multiplicar uno por 3.5, en donde 1 es el primer valor establecido de “x”, no te da el valor esperado, es decir, 11.50 pesos. Entonces, debes considerar cuánto le falta a 3.5 para llegar a 11.50. Se realiza una resta y se obtiene 8. Este número encontrado es la constante “b”.
Siguiendo la forma de la expresión algebraica y = ax + b, la expresión algebraica para calcular el costo a cobrar por la compañía de taxis “A”, sería y = 3.5x + 8y con ello, ya puedes elaborar la tabla de datos.
Se te invita a corroborar que dicha expresión algebraica sirve para encontrar cada valor de “y”, condicionado por los valores establecidos en “x”.
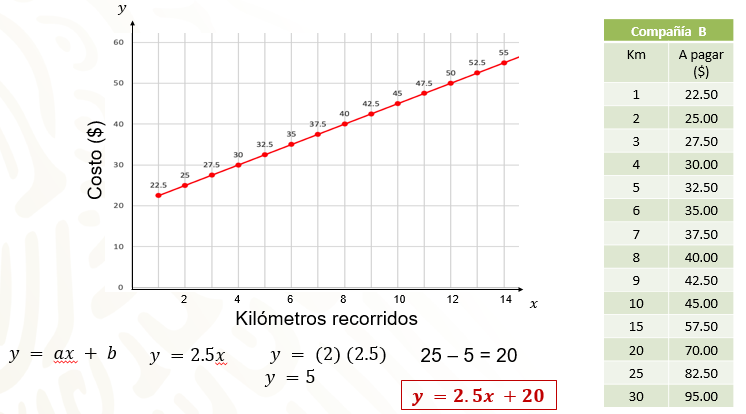
Ahora observa la variación entre intervalos iguales en la tabla correspondiente a la gráfica de la compañía “B”. Por ejemplo, ¿cuánto varia “y” cuando “x” incrementa de 1 en 1? Compara la variación cuando “x” vale 2, ¿qué valor le corresponde a “y”?
Después observa cuánto varía el valor de “y”, si “x” toma el valor de 3. Cuanto se incrementa dicha variación, ¿será la razón de cambio?
Para la primera comparación “y” pasa de 25.00 a 27.50 pesos; si observas la variación es de 2.50 pesos. Ahora observa la segunda variación, cuando “x” pasa de 3 a 4, es decir, “y” vale de 27.50 a 30 pesos, respectivamente. Nuevamente la variación es de 2.50 pesos. Como puedes ver, la variación permanece constante, por lo que puedes asegurar que cada valor que toma la variable “x” es multiplicado por 2.5, que será la constante “a”. Pero si haces la multiplicación 2 por 2.5, en donde 2 es el segundo valor establecido para “x”, no nos da el número esperado, 25 pesos. Entonces debes considerar cuánto le falta a 2.5 por 2, que son 5, para llegar a 25. Se realiza una resta y se obtiene 20. Este número corresponde a la constante “b”.
Siguiendo la forma de la expresión algebraica y = ax + b para la compañía de taxis “B” es y = 2.5x + 20
Corrobora que dicha expresión algebraica sirve para encontrar cada valor de “y”, condicionado por los valores establecidos en “x”.

Por último, puedes observar la variación entre intervalos iguales en la tabla, correspondiente a la gráfica de la compañía “C”, para establecer la razón de cambio y la expresión algebraica de la misma.
Para la primera comparación, “y” pasa de 10.50 a 14.50 pesos, si observas, la variación es de 4 pesos. Ahora observa la segunda variación; es decir, cuando a “x” se le asignan los valores de 4 y 5, “y” obtiene los valores 14.50 a 18.50 pesos, respectivamente, de nuevo la variación es de 4 pesos; es decir, la variación permanece constante. Por lo tanto, podrías asegurar que cada valor que toma la variable “x” es multiplicado por 4, que es la constante “a”. Pero si haces la multiplicación de 3 por 4, en donde 3 es el tercer valor establecido para “x”, no da el número esperado 10.50 pesos; entonces debes restarle a 10.5, 12, lo que da como resultado 1.5 negativo. Este número es la constante “b” que cumple la condición de la gráfica.
Siguiendo la forma de la expresión algebraica y = ax + b, la expresión algebraica para calcular el costo por cobrar por la compañía de taxis “C” es y = 4x – 1.5.
Se te invita a corroborar que dicha expresión algebraica sirve para encontrar cada valor de “y”, condicionado por los valores establecidos en “x”, para validar que los datos de la tabla son correctos.
Una vez terminado el análisis y desarrollo de las tres situaciones problemáticas presentadas, se puede concluir que muchas de las actividades cotidianas tienen implícitas relaciones que se pueden representar por una expresión algebraica, la cual puede ser determinada al reconocer los valores constantes y las variables involucradas en dicha expresión algebraica.
Después se puede elaborar una tabla para observar su comportamiento e incluso usar la representación gráfica que permita en un solo vistazo entender dicha situación. Asimismo, a partir de tablas de datos se puede encontrar la expresión algebraica que la representa y obtener su gráfica; o como en la última actividad, a partir de gráficas en un mismo plano, poder rescatar los datos para obtener la tabla y, a su vez, a partir de ésta encontrar la expresión algebraica que incluya los valores representados.
De esta forma se puede concluir que la expresión algebraica lineal, la tabla elaborada a partir de la relación entre las variables involucradas y la gráfica de estos datos en el plano cartesiano son equivalentes una con otra.
Has concluido la sesión del día de hoy.
El reto de hoy:
¿Olvidaste dar con la pista para solucionar el juego el “Salto de la rana”?
Reflexiona: las fichas rojas deben ocupar los lugares de las azules y viceversa.
La pista es que por ningún motivo deberás tener dos fichas del mismo color juntas; de lo contrario, habrás perdido la oportunidad de hacerlo a la primera y deberás colocar nuevamente las fichas como en un principio. Éxito.
Explora tu libro de texto y también consulta otras fuentes para aclarar las dudas que pudieran surgir. En tu libro de texto de Matemáticas puedes encontrar más actividades relacionadas con relaciones de variación lineal para practicar el trabajo realizado en esta sesión.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion