Sistema de dos ecuaciones lineales con dos incógnitas y el método gráfico

Sistema de dos ecuaciones lineales con dos incógnitas y el método gráfico

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: plantear y resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas.

¿Qué vamos a aprender?

En esta sesión, profundizarás en la resolución de problemas de sistemas de dos ecuaciones lineales con dos incógnitas, mediante el método gráfico. También, identificarás que al resolver algunos sistemas de ecuaciones lineales mediante este método puede suceder que:

• Algunos tienen solución única,
• otros tienen un número infinito de soluciones y,
• algunos más no tienen solución.

Recuerda que, para resolver el sistema de dos ecuaciones lineales con dos incógnitas mediante el método gráfico, debes realizar una serie de pasos, ya que se trata de un método, y como todo método implica un orden.

¿Qué hacemos?

Resuelve la primera situación-problema.

Situación-problema: Cabo San Lucas

Del Puerto de Cabo San Lucas México, salen dos barcos, el barco México 1, navega con una trayectoria de: x + y = -88; el barco México 2, navega con una trayectoria de: 2x + 2y = -176.

¿En qué punto se encontrarán los dos barcos?

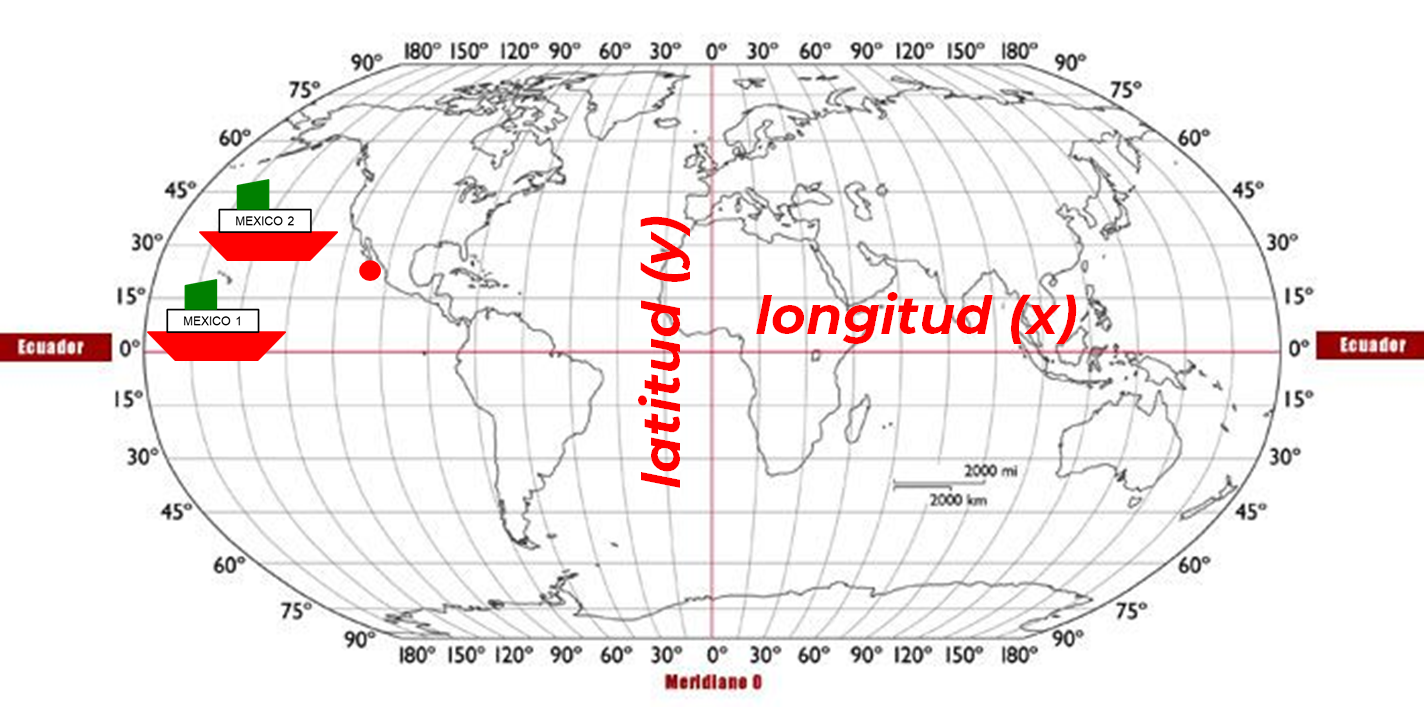
El primer paso consiste en el planteamiento del Sistema de Ecuaciones Lineales, con base en los datos incluidos en el enunciado del problema propuesto. En esta situación-problema, ya está planteado el sistema de ecuaciones.

El barco México 1, navega con una trayectoria de: x + y = -88; y el barco México 2, navega con una trayectoria de: 2x + 2y = -176. Por lo tanto, el sistema de ecuaciones del problema “Cabo San Lucas”, queda establecido como:

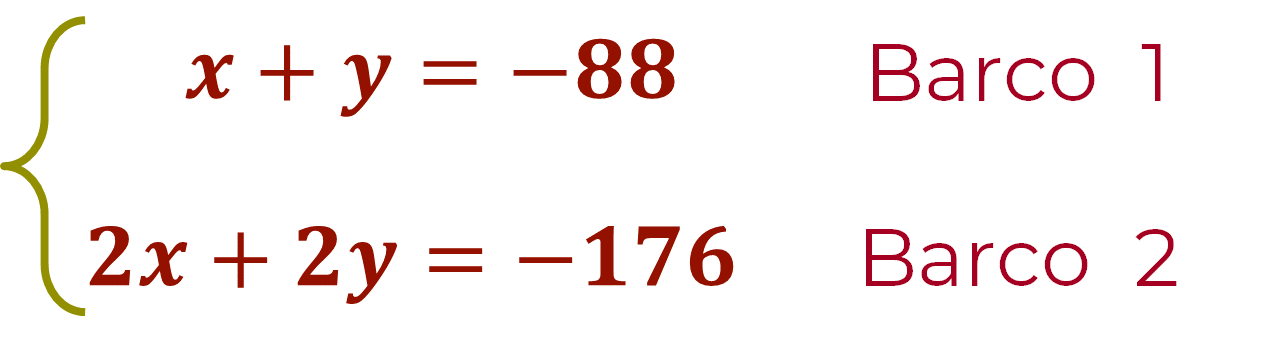
Donde:

x: representa la longitud en grados.

y: representa la latitud en grados.

Pero ¿por qué es un sistema de ecuaciones?

Se considera un sistema, porque hay una relación entre las ecuaciones, es decir, los grados de longitud y los grados de latitud están relacionados con la trayectoria de cada barco. Por lo tanto, el sistema de dos ecuaciones lineales con dos incógnitas permite resolver la situación-problema.

Continúa con el paso dos: despejar la incógnita “y” en ambas ecuaciones. Para encontrar la solución del sistema, es común que primero se exprese cada ecuación lineal en términos de “y”

Despeja “y” en la ecuación 1

Para despejar la incógnita “y”, utilizarás las propiedades de los números y las operaciones con números enteros, entonces se aplica el inverso aditivo de “x” en ambos miembros de la ecuación:

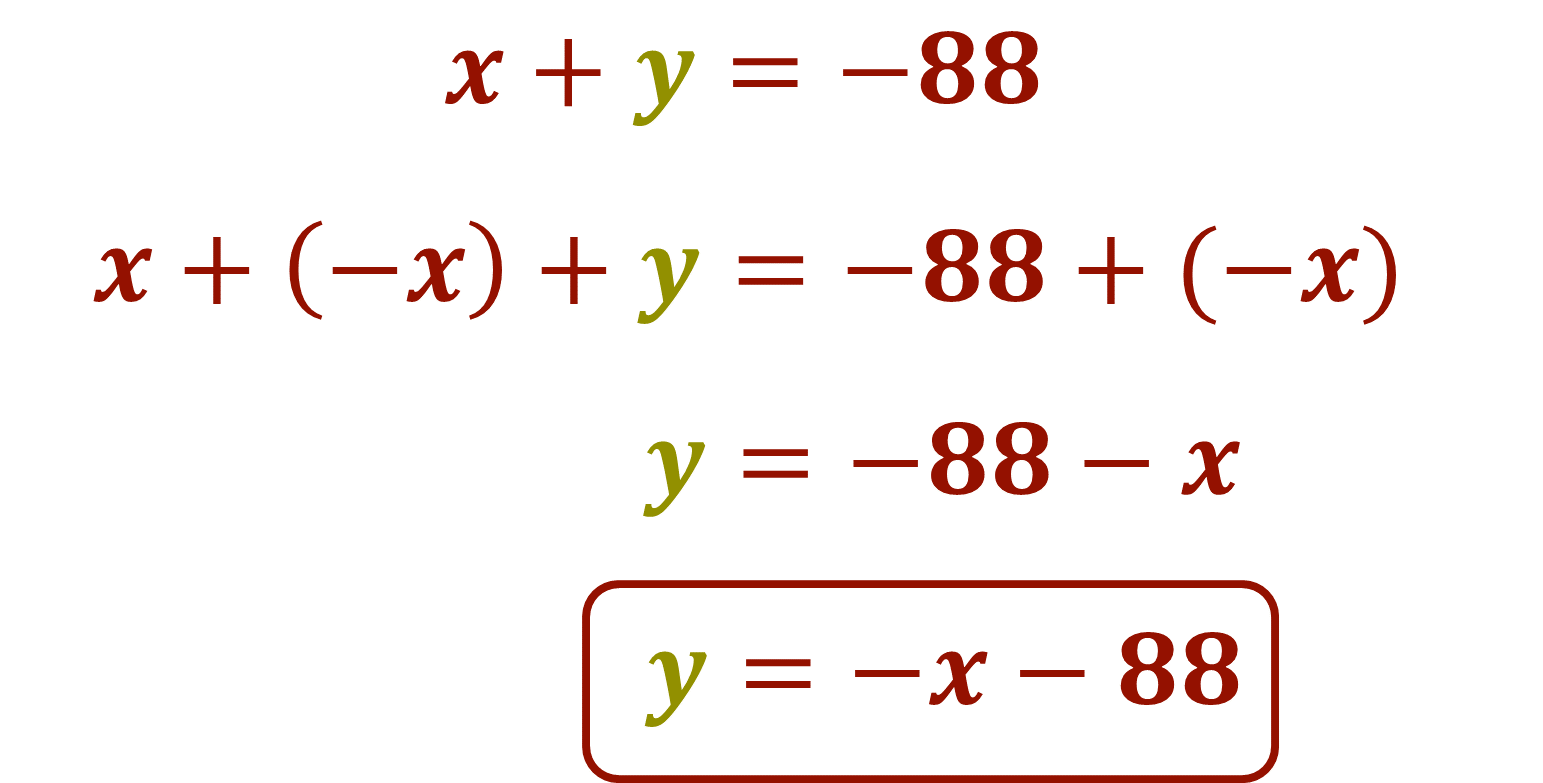
Por lo tanto, para la ecuación 1: y = -x -88

Ahora, despeja a la incógnita “y” en la ecuación 2:

Para despejar la incógnita “y”, utilizarás las propiedades de los números y las operaciones con números enteros, entonces se suma el inverso aditivo de “2x” en ambos miembros de la ecuación, de tal forma que se elimina a “2x” al sumar “2x” negativo del primer miembro de la ecuación, obteniendo la siguiente igualdad:

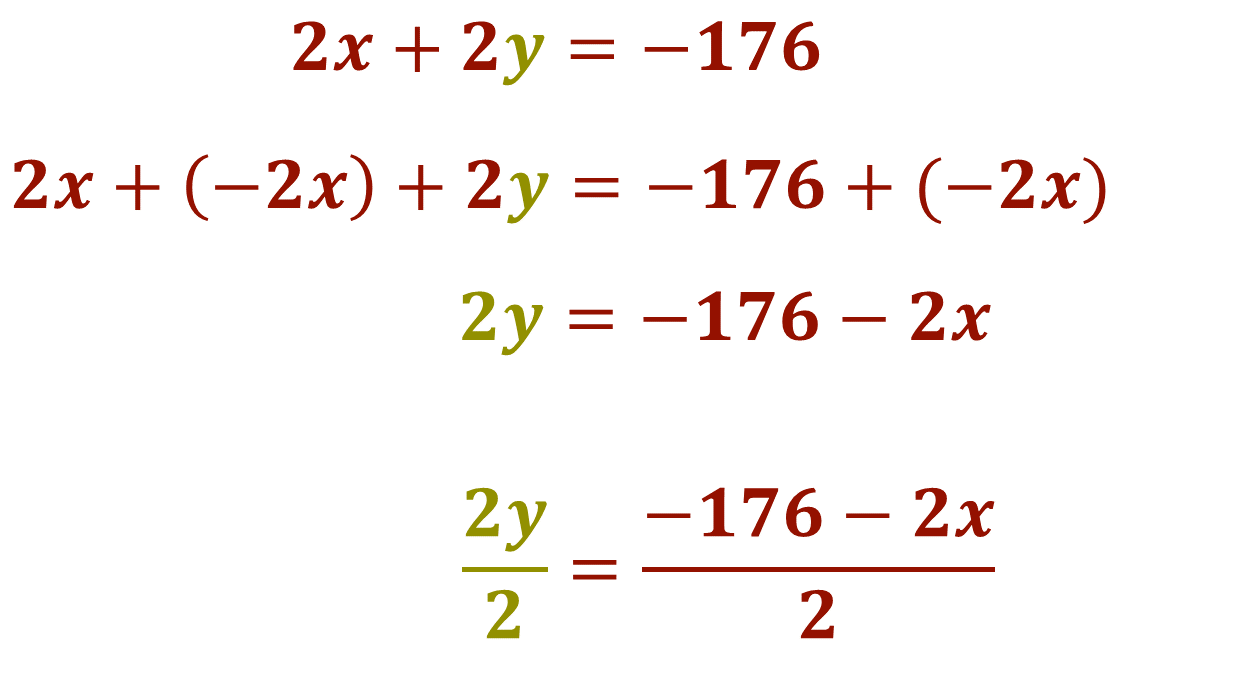
Aplicando la propiedad de la igualdad, se dividen ambos miembros de la ecuación entre el coeficiente de “y” que es 2, por lo tanto, queda de la siguiente forma:

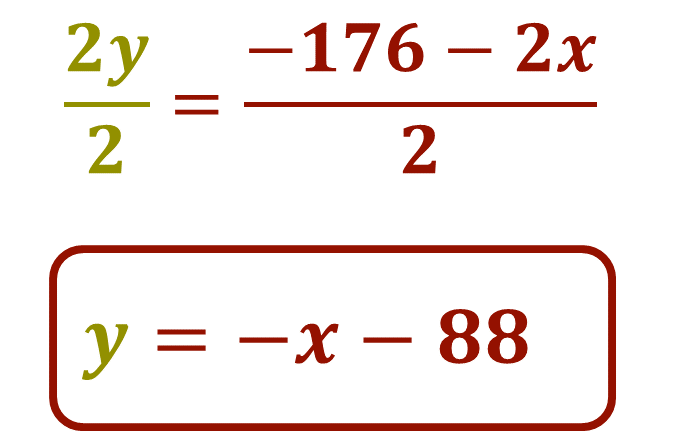
Obteniendo: y = -x -88

¿Qué representa la ecuación dos en la situación-problema?

Permite representar el trayecto del barco 2, dados los valores de “x”. Has terminado el despeje de la incógnita “y” en las dos ecuaciones del sistema. Por lo tanto, queda el Sistema de Ecuaciones con despejes de “y”:

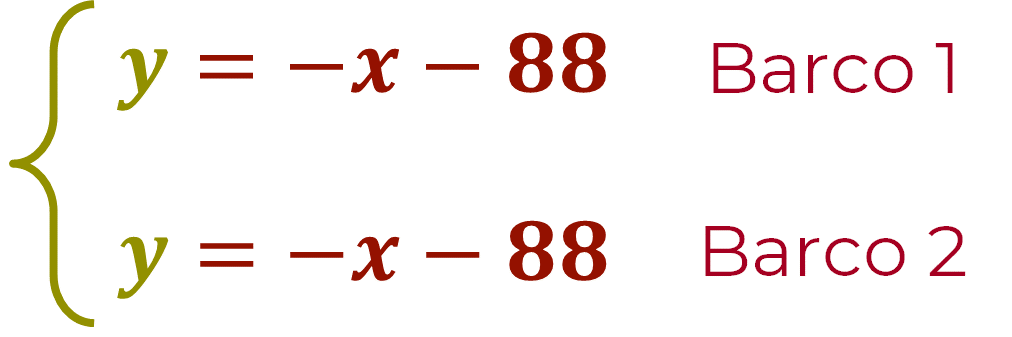
¿Qué observas en ambas ecuaciones? Son iguales, es decir que las ecuaciones son equivalentes y dependientes.

Y, ¿qué representa que sean equivalentes o dependientes en el contexto del problema? Representa que la trayectoria del barco 1 y del barco 2, es la misma, es decir, llevan el mismo trayecto

Continúa con el paso 3 para justificarlo.

Asignarás valores a la literal “x” y los sustituirás en los correspondientes despejes de “y”. A partir de la ecuación equivalente, y = -x -88, los valores de “x”, proporcionados por torre de control son: -105, -90 y -78

¿Qué significan estos valores asignados a “x”? La longitud en grados.

De la ecuación equivalente: y = -x -88, se obtienen los valores de “y” en las ecuaciones 1 y 2, por lo tanto:

¿Recuerdas qué significan los valores de “x” y de “y”?

x: significa la longitud del trayecto del barco.

y: significa la latitud del trayecto del barco.

Ahora, organiza los datos obtenidos de “x” y “y” en una tabla.

Organizando datos, se tiene en la primera columna los valores de “x” longitud, en la segunda columna los valores obtenidos de “y” latitud.

¿Cómo se forman los puntos coordenados? Cada punto se nombra utilizando letras mayúsculas y colocando dentro del paréntesis los valores de “x” y de “y”, siempre el primer valor será el de las abscisas o “x” y el segundo valor será el de las ordenadas o “y”. En la tercera columna se colocan los puntos coordenados, es decir el trayecto del barco y quedan definidas como:

A (-105,17)

B (-90, 2)

C (-78, -10)

Observa cómo queda la tabla:

Ahora, sigue con el paso cuatro. A partir de la ubicación del Puerto de Cabo San Lucas, se ubican los puntos coordenados (x, y), que se obtuvieron mediante la ecuación equivalente: y = -x -88, en el plano cartesiano, para el:

A (-105,17)

B (-90, 2)

C (-78, -10)

Ahora, traza una línea sobre los puntos.

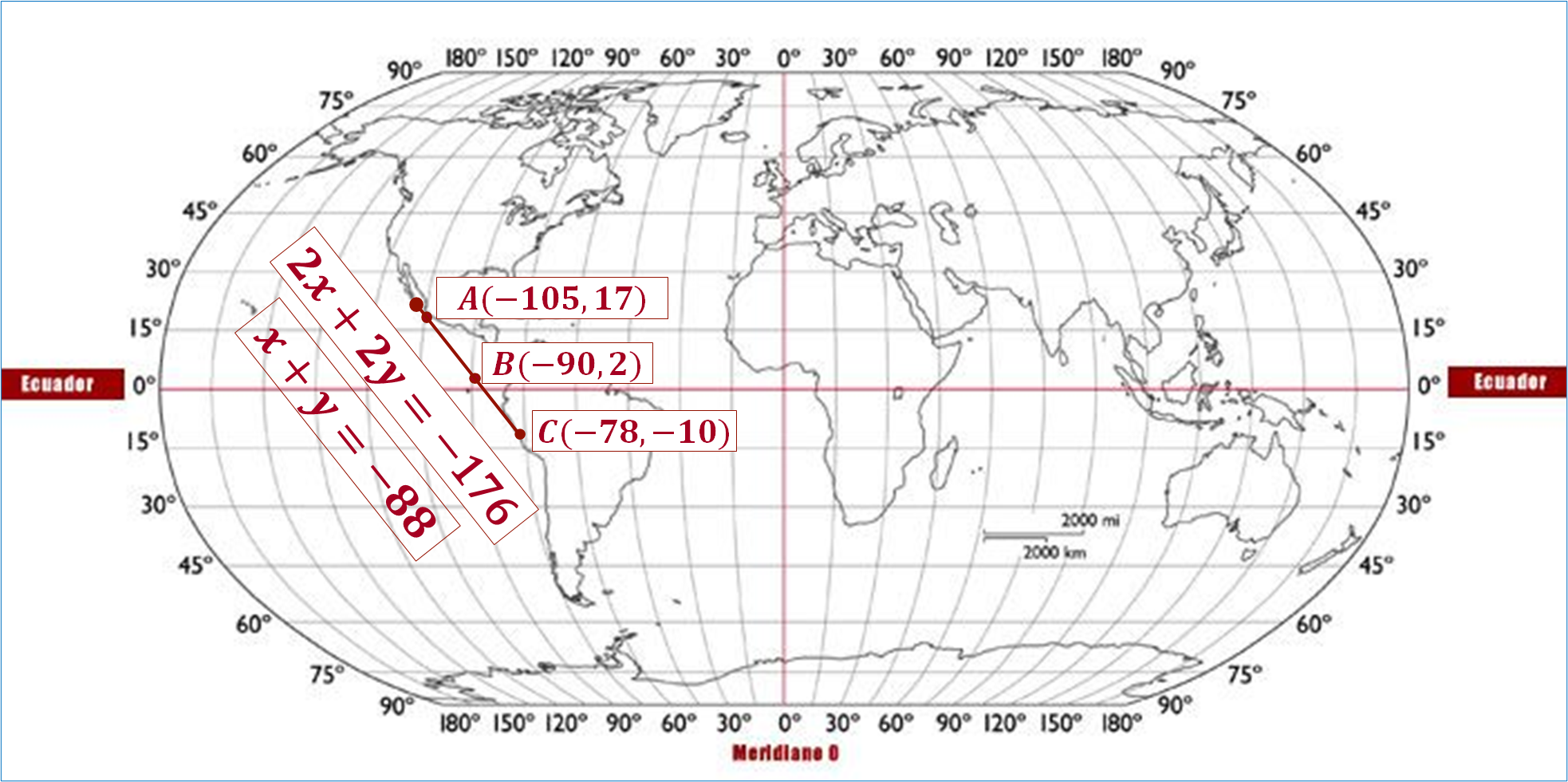
Se obtiene una línea recta que representa el comportamiento de la ecuación, es decir, el trayecto de los dos barcos.

Ahora es momento de relacionar e interpretar las gráficas resultantes para identificar la solución del sistema y, con ello, la solución del problema.

¿Qué representa la gráfica?

En la gráfica, se puede observar que no hay intersección entre las dos líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas del sistema, dichas líneas están una encima de la otra, por lo tanto, se afirma que el sistema tiene una infinidad de soluciones, es decir, que los barcos llevan la misma trayectoria, por lo tanto:

¿En qué punto se encontrarán los dos barcos?

Los barcos se pueden encontrar en cualquier punto del trayecto, es decir las dos ecuaciones son dependientes, ya que la representación de ambas es la misma recta, por lo tanto, cualquier punto de una de ellas satisface a la otra.

Para fortalecer lo aprendido, analiza otra situación problema.

Situación-problema: Sierra Leone-Cape Town

Del Puerto de Sierra Leone, África, sale el barco 1 que navega con una trayectoria de x + y = -4; y del Puerto Cape Town, ubicado al sur de África, sale el barco 2 que navega con una trayectoria de x + y = -16. ¿En qué punto del plano se encontrarán los dos barcos?

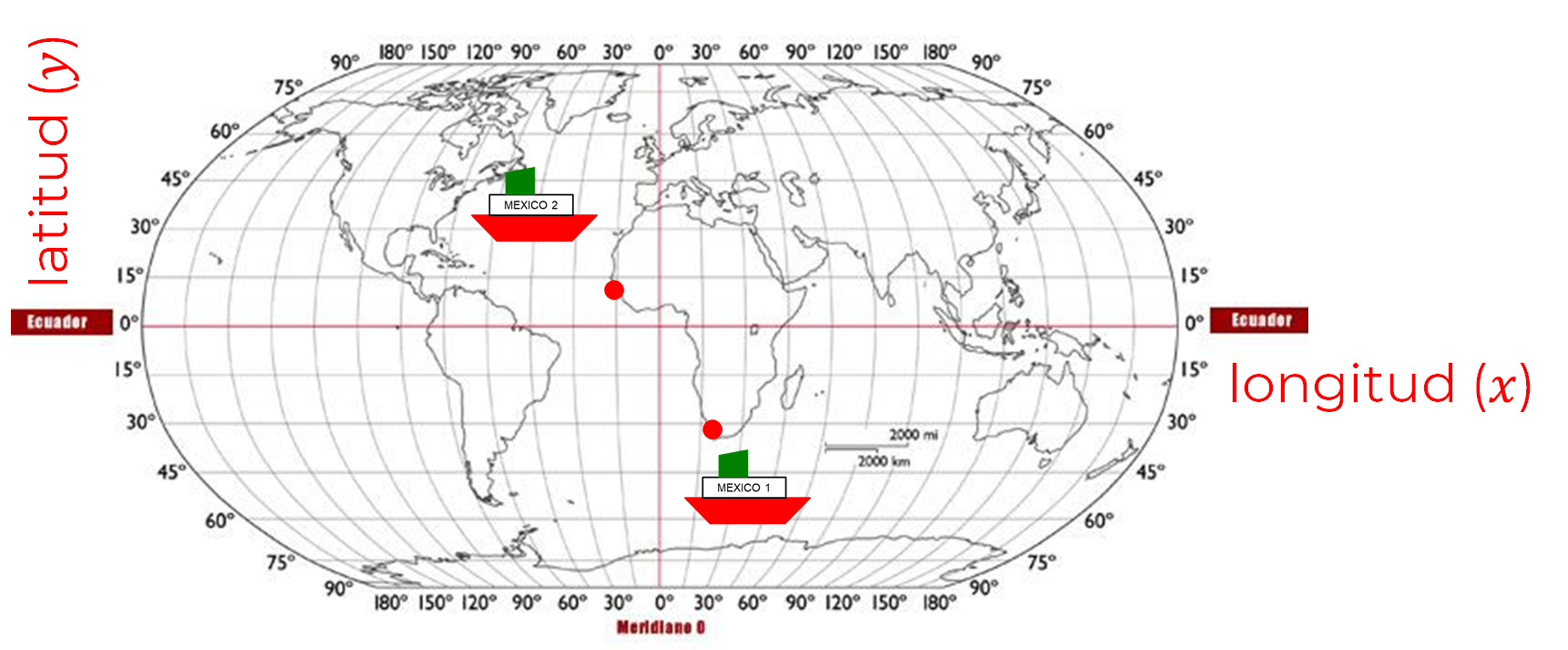
De acuerdo con la segunda situación-problema, ¿cuál es el sistema de ecuaciones planteado?

El sistema de ecuaciones del problema “Sierra Leone-Cape Town”, queda establecido como:

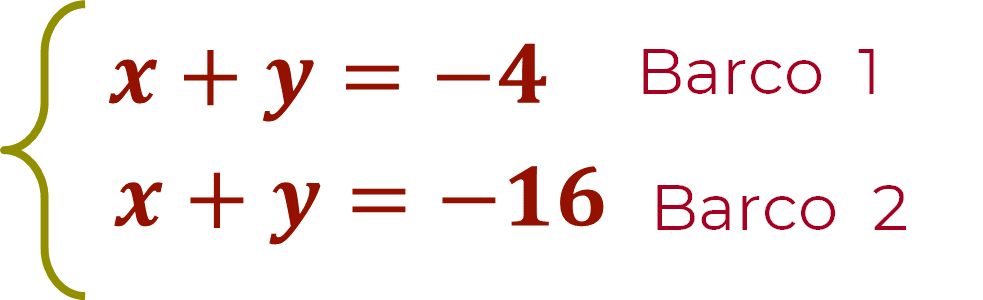
Donde:

x: representa la longitud en grados.

y: representa la latitud en grados.

Ahora, despeja la incógnita “y” de la ecuación 1:

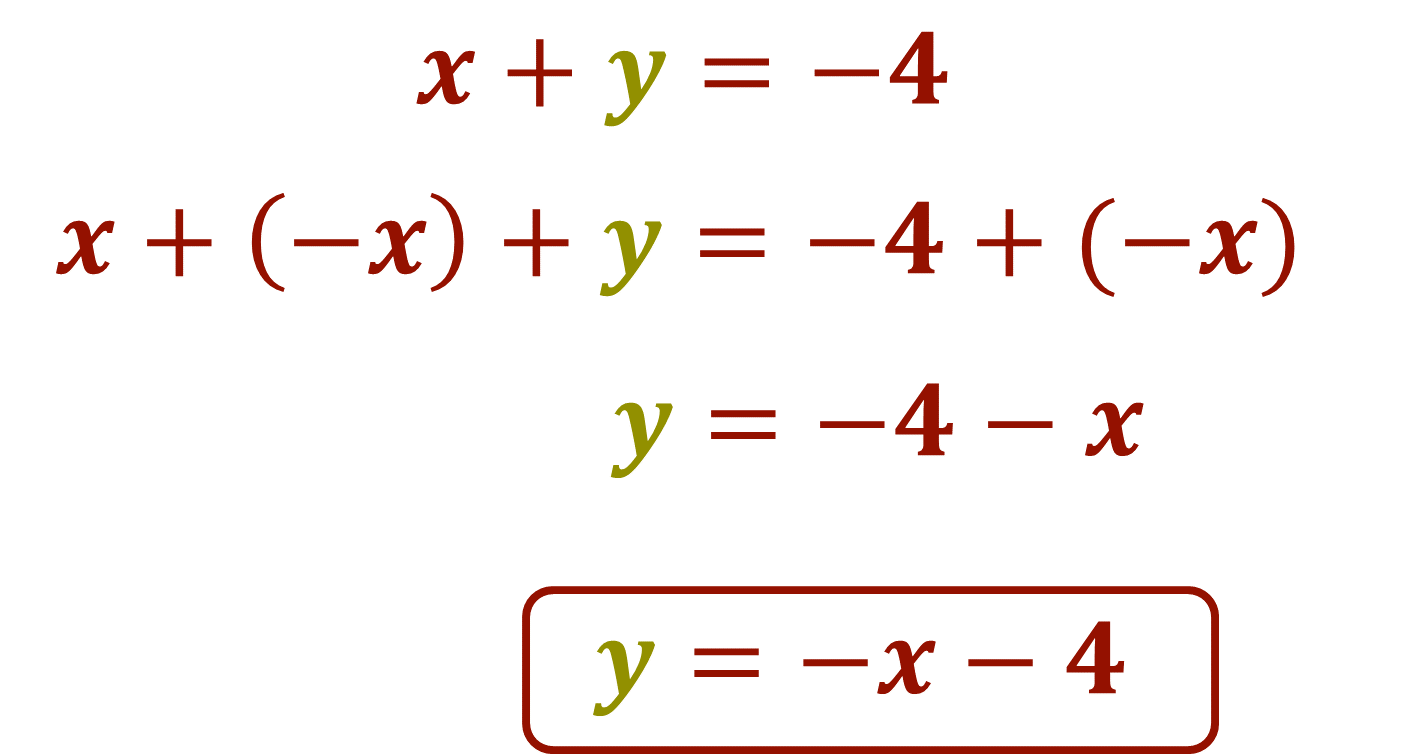
Por lo tanto, para la ecuación 1 queda, y = x -4. Esta ecuación ayudará a calcular el trayecto del barco 1.

Ahora despeja la incógnita “y” de la segunda ecuación:

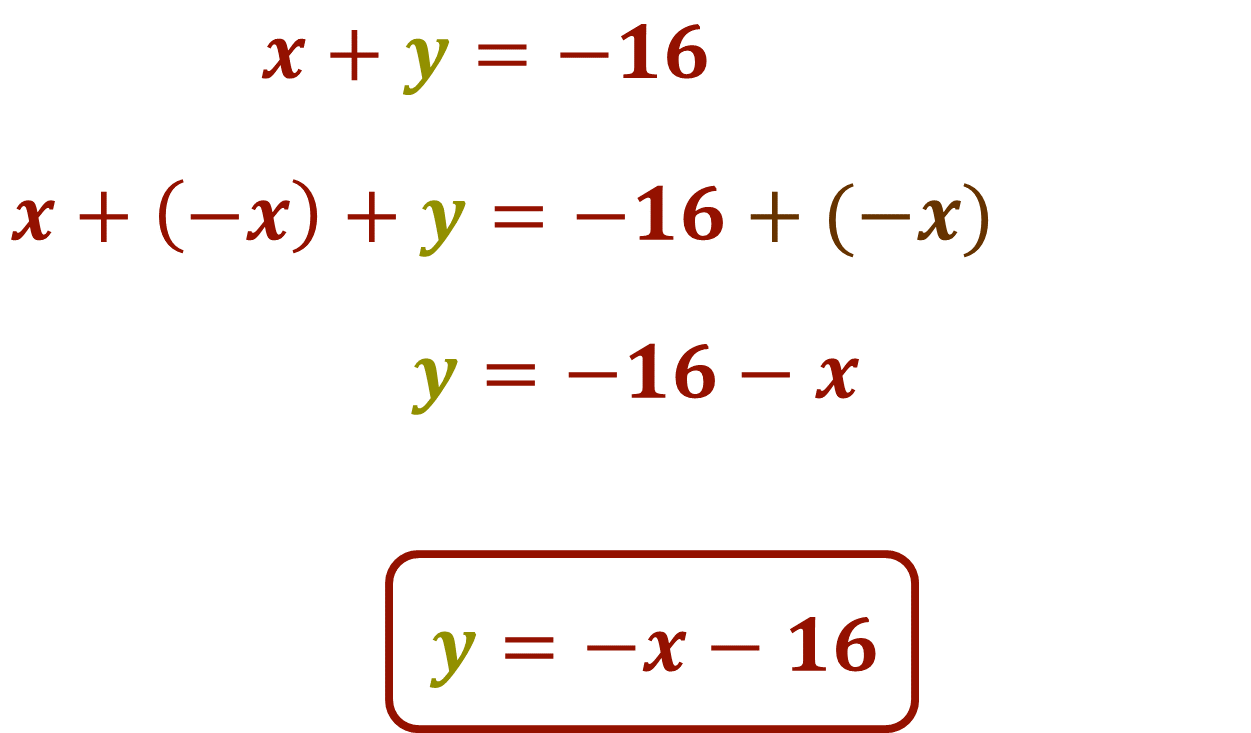
Por lo tanto, la ecuación 2 es, y = -x -16. La ecuación dos ayudará a calcular el trayecto del barco 2.

Hemos terminado el despeje de la incógnita “y” en las dos ecuaciones del sistema. El sistema de ecuaciones con despejes de “y”, queda como:

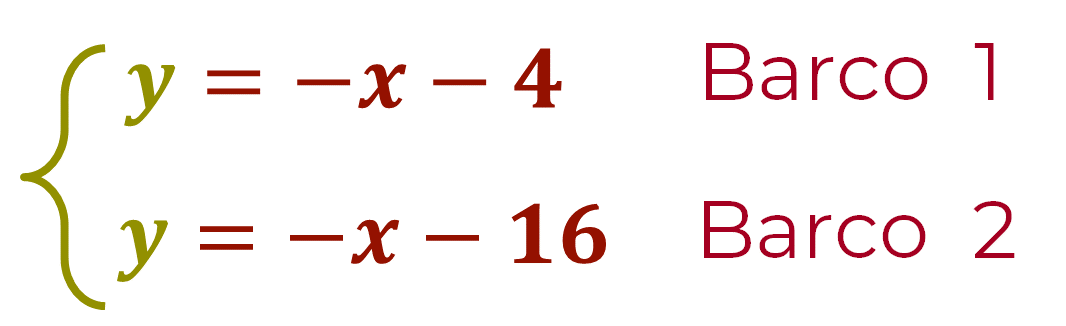
Ahora se asignan valores a la literal “x” y se sustituyen en los correspondientes despejes de “y”. A partir de la ecuación, y = -x -4, los valores de “x”, proporcionados por torre de control son: -30 y -45, es decir, la longitud en grados.

A partir de la ecuación 1: y = -x -4, se obtienen los valores de “y”. Por lo tanto:

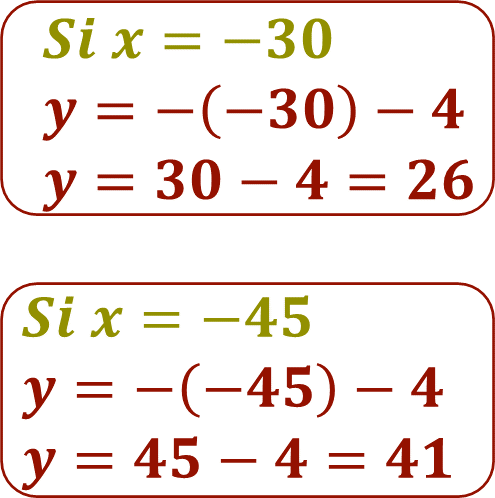
Ahora organiza los datos obtenidos de “x” y “y” en una tabla.

En la primera columna se registran los valores de “x” que representan la longitud. En la segunda columna, los valores obtenidos de “y”, es decir, la latitud. Y en la tercera columna se registran los puntos coordenados del trayecto del barco:

A (30 negativo, 26)

B (45 negativo, 41)

La tabla queda de la siguiente manera:

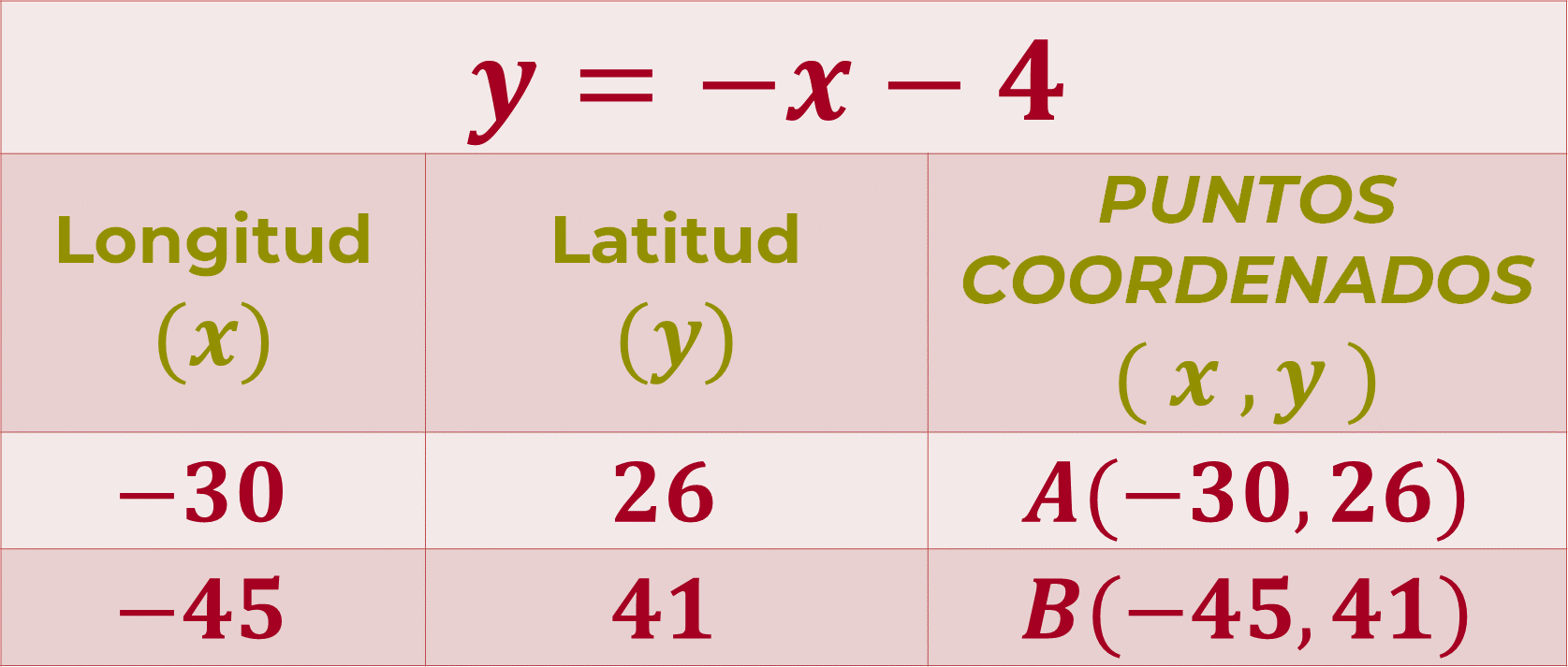
A partir de la ubicación del Puerto Sierra Leone, se ubican los puntos coordenados (x, y), que se obtuvieron mediante la ecuación 1: y = -x -4, en el plano cartesiano, para el:

Punto A (-30, 26)

Punto B (-45, 41)

Ahora, traza una línea sobre los puntos, ¿qué tipo de recta se obtiene?

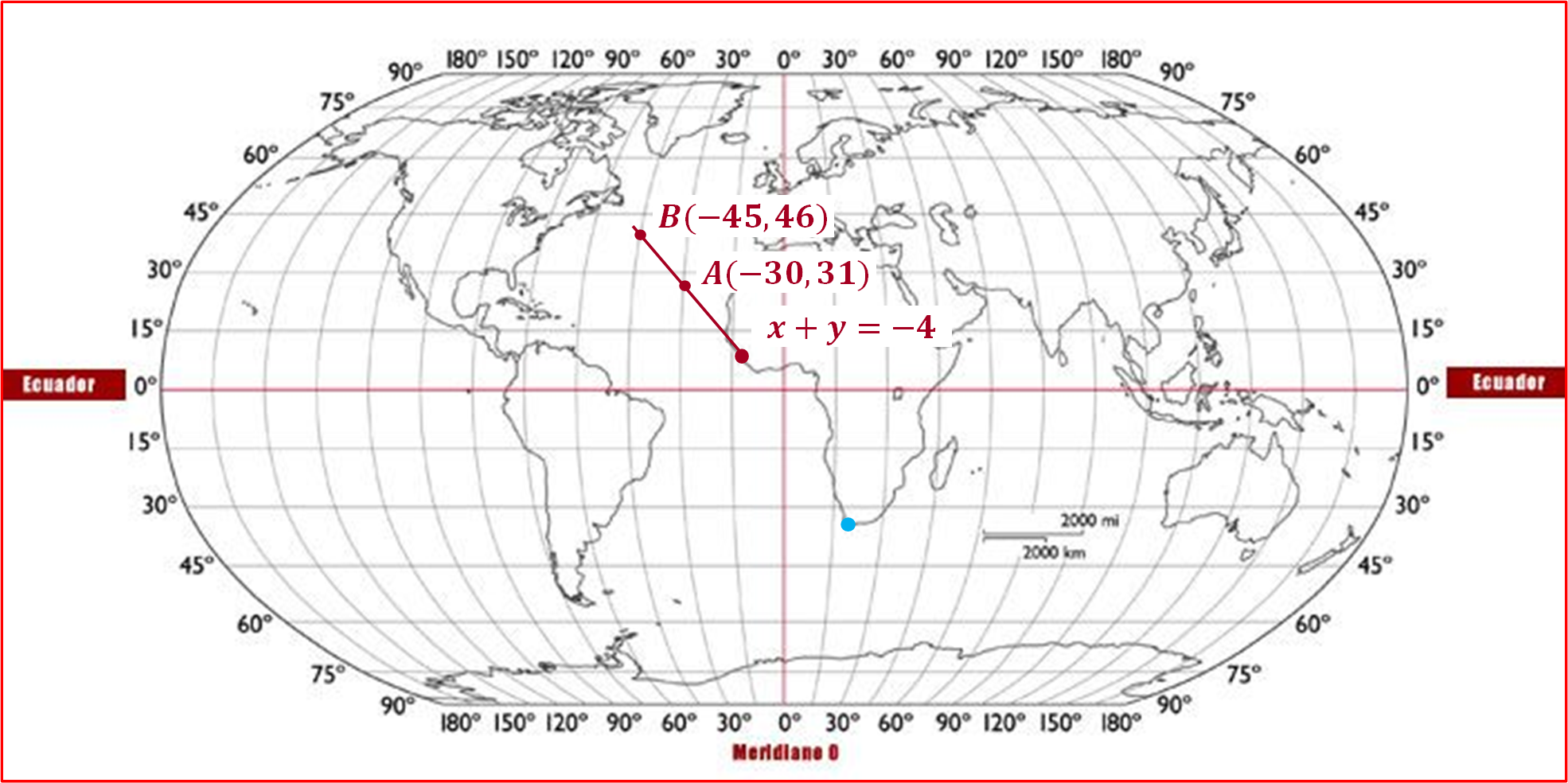
Se obtiene una línea recta que representa el comportamiento de la ecuación 1, es decir el trayecto del barco 1

Ya que se tiene el trayecto del barco 1, vas a asignar valores a la literal “x” y sustituirlos en el correspondiente despeje de “y”, en la ecuación 2, y = -x -16. Los valores de “x”, proporcionados por torre de control son: 0, -15, -30 y -45

A partir de la ecuación 2: y = -x -16, se obtienen los valores de “y”. Por lo tanto:

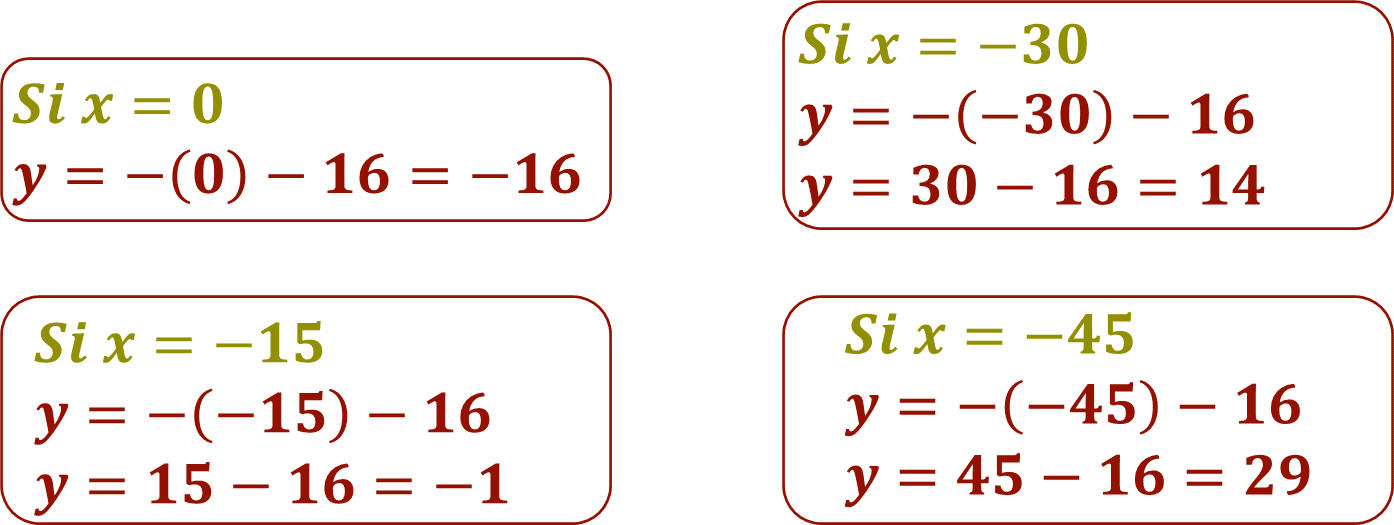
Organiza los datos obtenidos de “x” y “y” en una tabla.

Organizando datos, se tiene en la primera columna los valores de “x” longitud, en la segunda columna los valores obtenidos de “y” latitud. En la tercera columna los puntos coordenados del trayecto del barco quedan definidos como;

A (0,-16)

B (-15, -1)

C (-30, 14)

D (-45, 29)

A partir de la ubicación del Puerto Cape Town, se ubican los puntos coordenados (x, y), que se obtuvieron mediante la ecuación dos: y = -x -16, en el plano cartesiano, para el:

A (0,-16)

B (-15, -1)

C (-30, 14)

D (-45, 29)

Observa cómo queda la tabla:

Ahora, traza una línea sobre los puntos, ¿qué tipo de recta se obtiene?

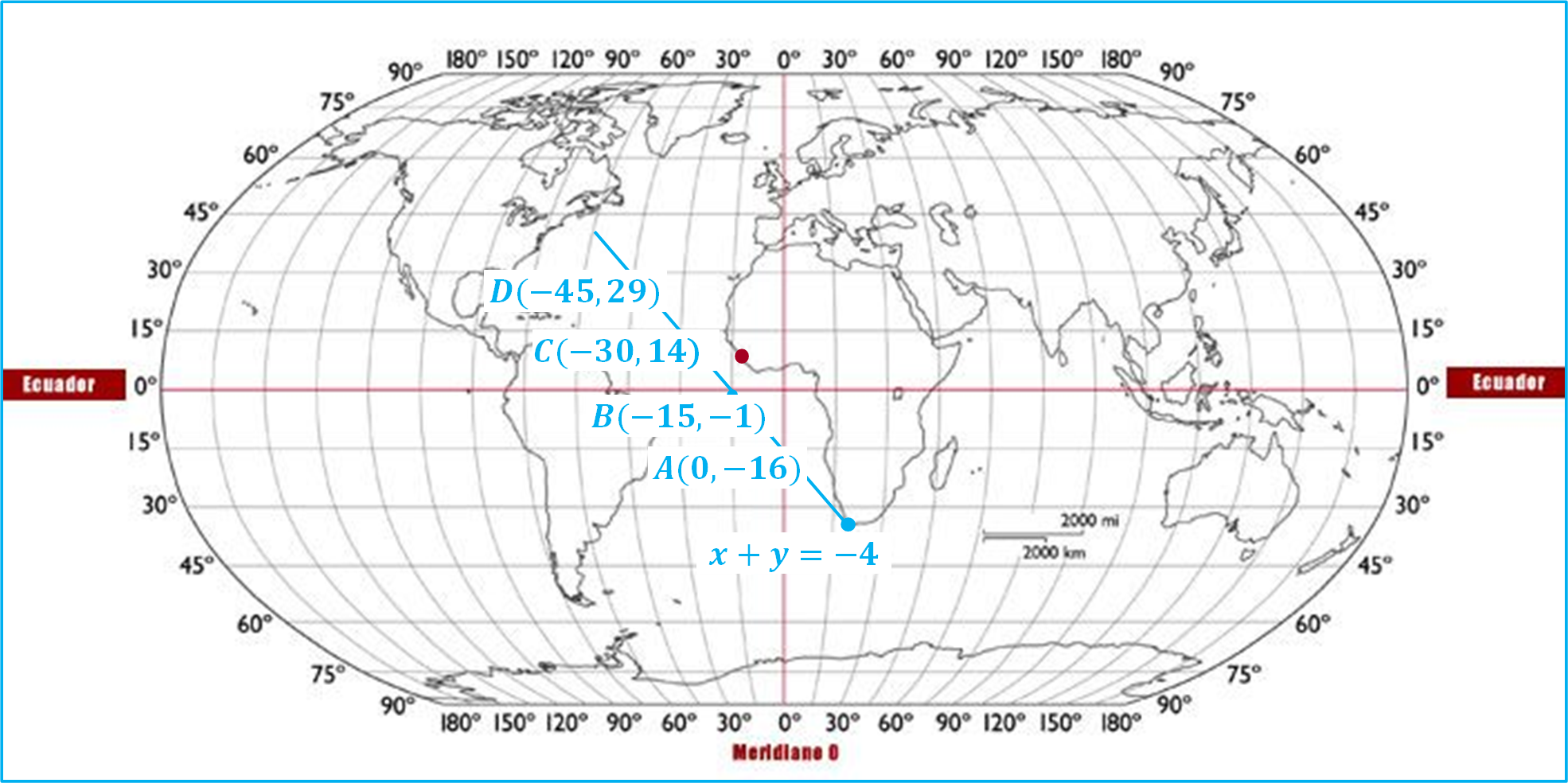
Se obtiene una línea recta que representa el comportamiento de la ecuación 2, es decir, el trayecto del barco 2

Ahora es momento de relacionar e interpretar las gráficas resultantes para identificar la solución del sistema y con ello la solución del problema.

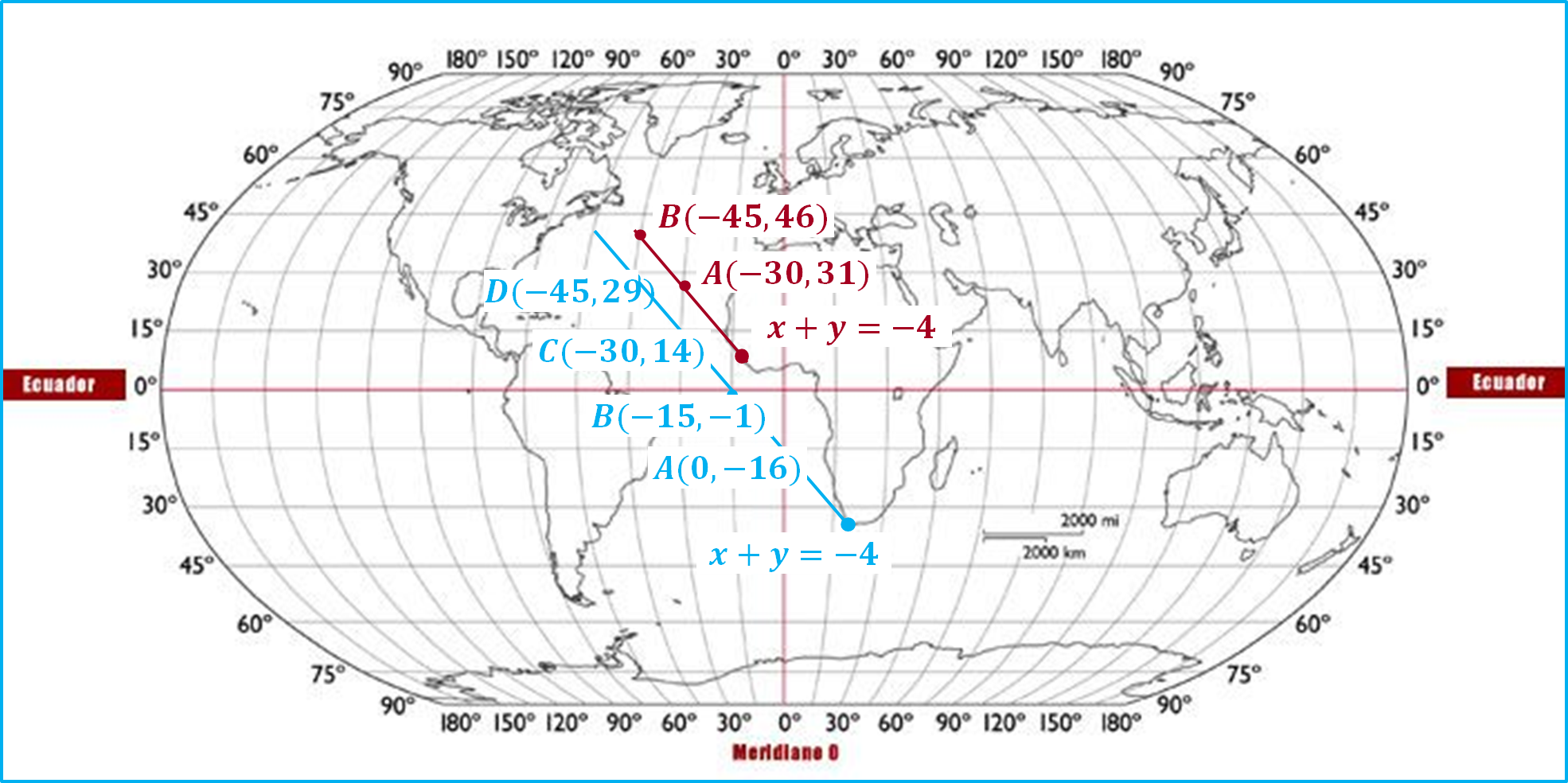
En la gráfica, se puede observar que no hay intersección entre las dos líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas del sistema, dichas líneas son paralelas entre sí, por lo tanto, se afirma que el sistema no tiene solución, es decir, que los barcos llevan diferentes trayectorias y no se encontrarán, no forman parte de un sistema de ecuaciones “2 x 2”, ya que no hay relación.

Para concluir, resuelve la siguiente última situación-problema.

Situación-problema: Bunbury-Madagascar

Del Puerto Bunbury Australia, sale el barco 1, navega con una trayectoria de: x + y = 82. Del Puerto Tolanaro Madagascar, sale el barco 2, que navega con una trayectoria de: -x + y = -71

¿En qué punto del plano se encontrarán los dos barcos?

El sistema de ecuaciones del problema “Bunbury-Madagascar” queda establecido como:

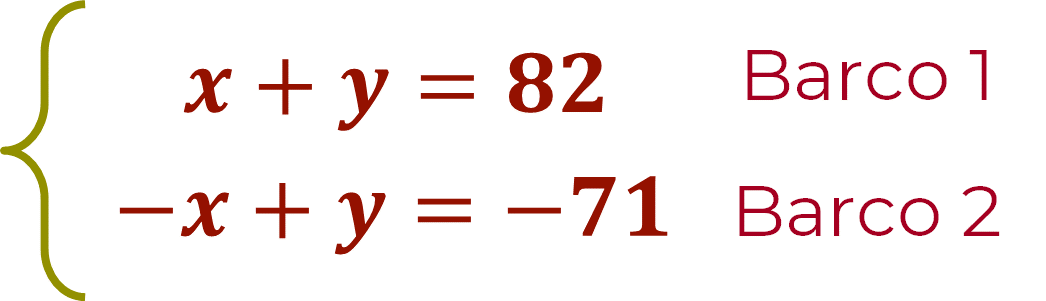
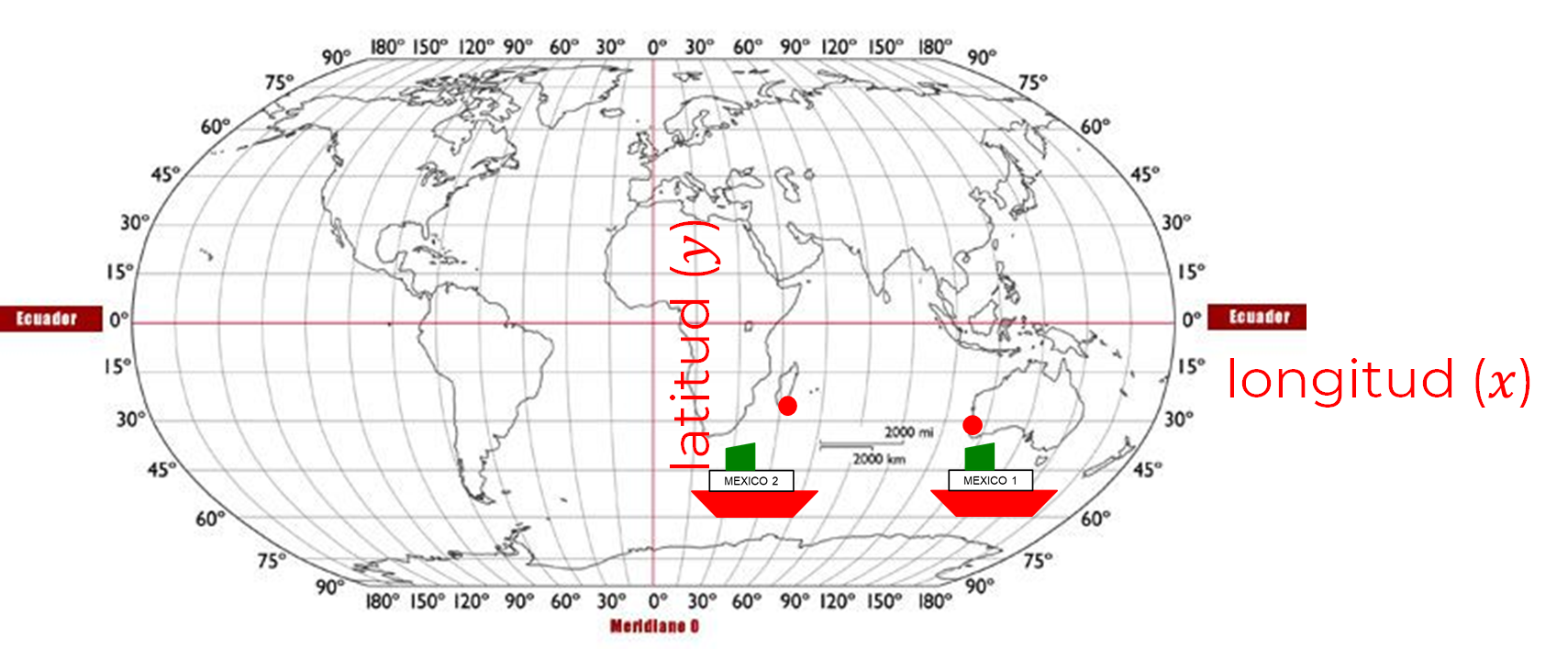
Donde:

x: representa la longitud

y: representa la latitud

Se despeja la incógnita “y” de la ecuación 1 y de la ecuación 2. Por lo tanto, queda el sistema de ecuaciones con despejes de “y”, “Australia-Madagascar”, como:

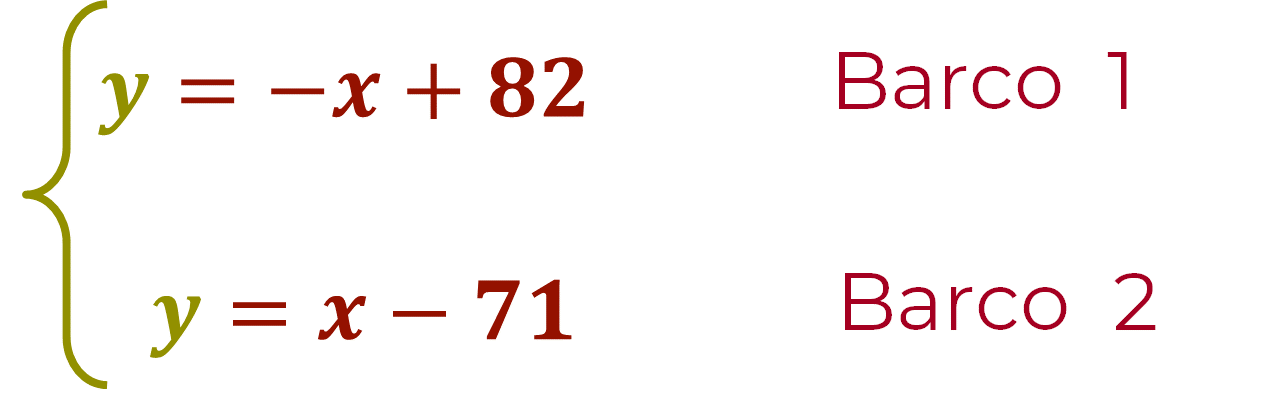
Se asignan valores a la literal “x” y se sustituyen en los correspondientes despejes de “y”. En la ecuación: y = -x + 82, los valores de x son: 105, 90 y 75

A partir de la ecuación 1, y = -x + 82, se obtienen los valores de “y”.

Por lo tanto:

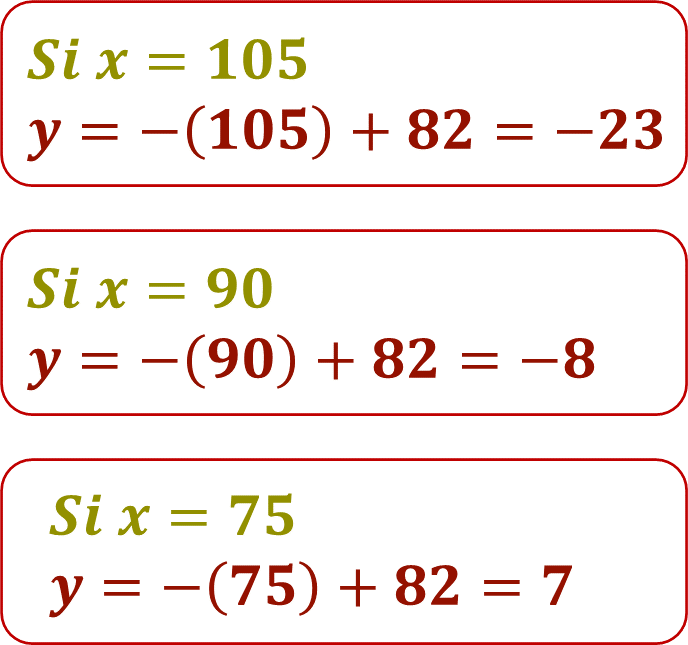
Se organizan los datos en una tabla. Los puntos coordenados del trayecto del barco se definen como:

A (105, -23)

B (90, -8)

C (75, 7)

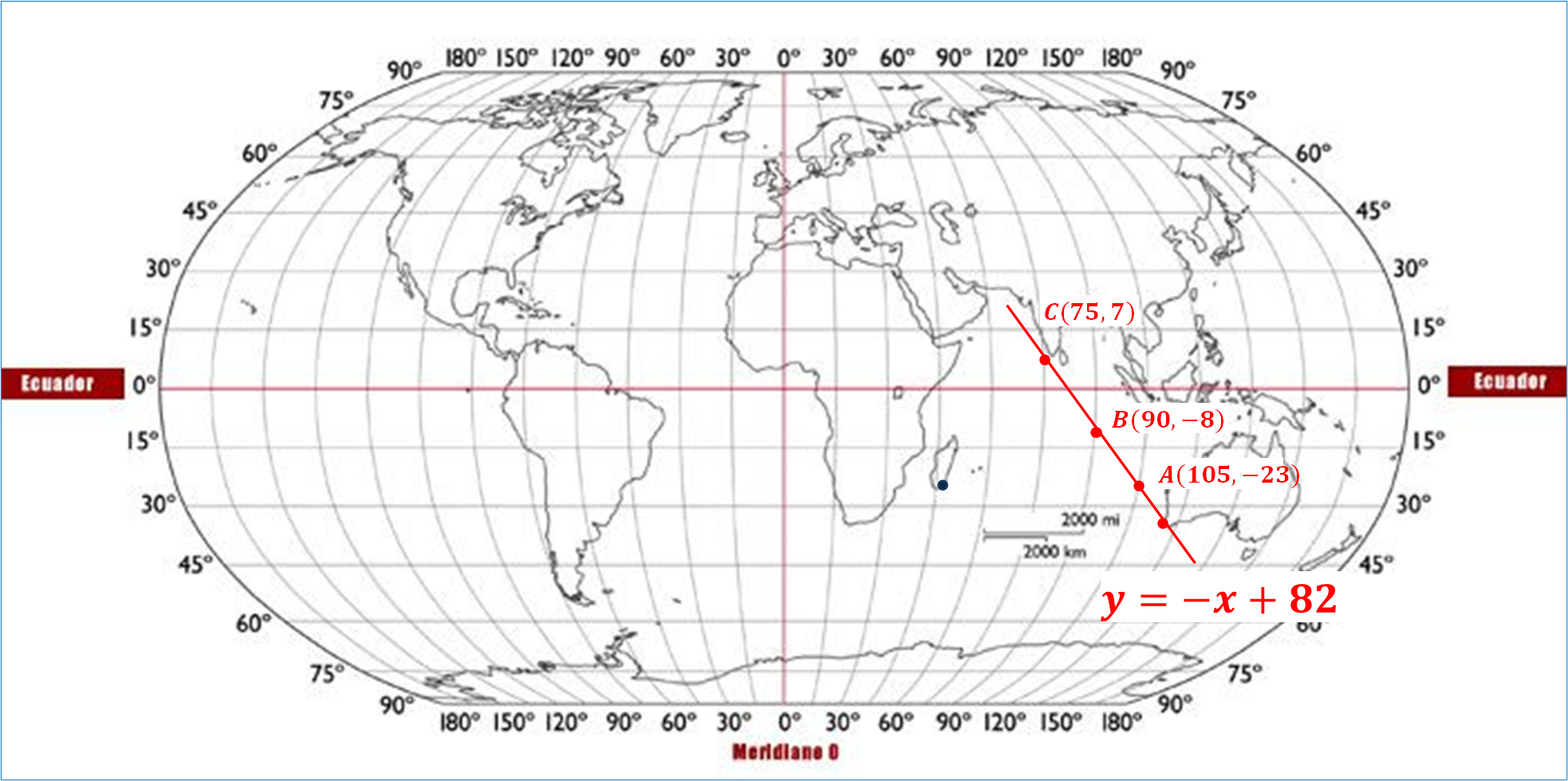
A partir de la ubicación del Puerto de Bunbury, se ubican los puntos coordenados (x, y), que se obtuvieron en la ecuación 1: y = -x + 82, en el plano cartesiano, para el punto:

A (105, -23)

B (90, -8)

C (75, 7)

La tabla queda de la siguiente manera:

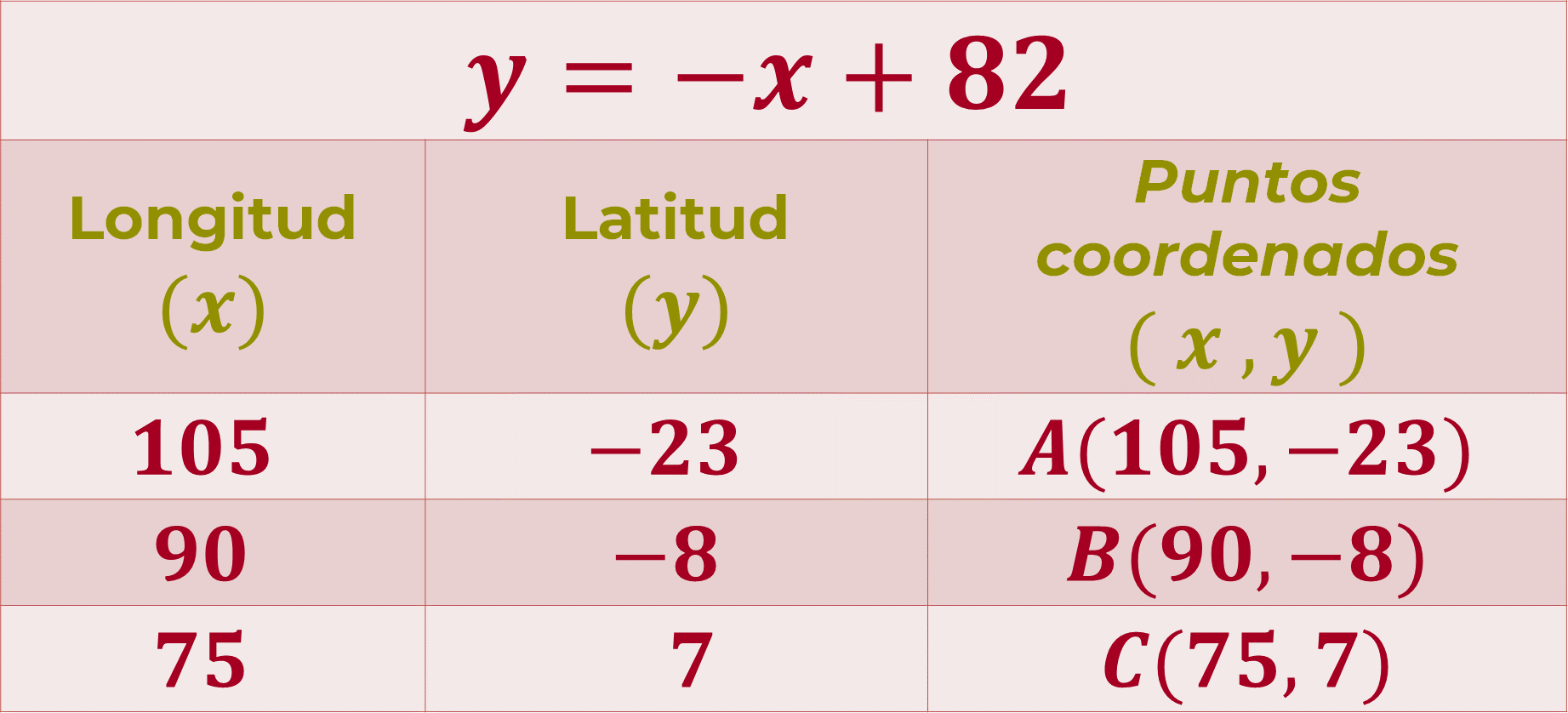
Se obtiene una línea recta que representa el comportamiento de la ecuación uno, es decir, el trayecto del barco 1

Ahora se asignan valores a la literal “x” y se sustituyen en el correspondiente despeje de “y”- En la ecuación 2: y = x - 71, los valores de “x” son 60 y 75

A partir de la ecuación 1, y = x - 71, se obtienen los valores de “y”

Por lo tanto:

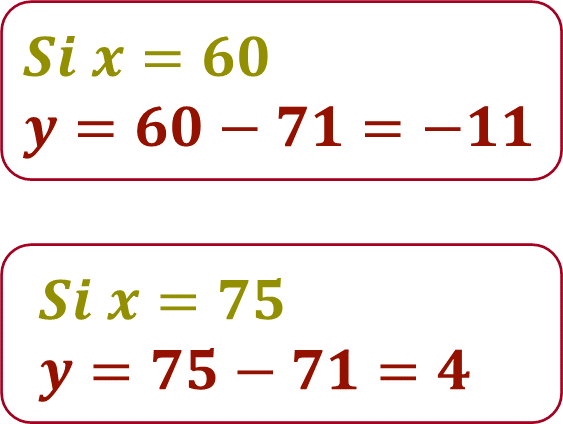
Se organizan los datos en una tabla, y los puntos coordenados del trayecto del barco 2 quedan definidos como:

A (60, -11)

B (75, 4)

A partir de la ubicación del Puerto de Madagascar, se ubican los puntos coordenados (x, 𝑦), que se obtuvieron mediante la ecuación 1 y = x - 71, en el plano cartesiano, para el punto:

A (60, -11)

B (75, 4)

La tabla queda de la siguiente manera:

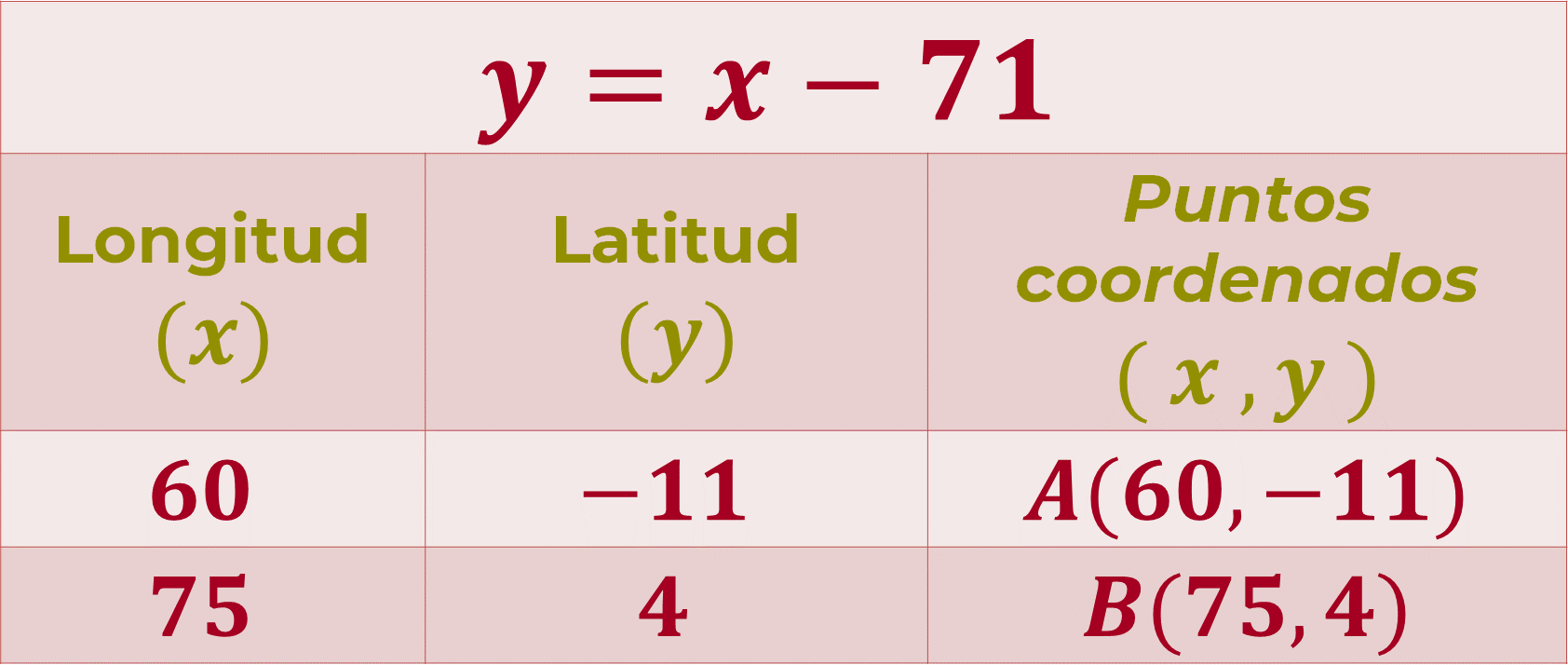
Ahora, traza una línea sobre los puntos y se obtiene una línea recta que representa el comportamiento de la ecuación 2, es decir, el trayecto del barco 2

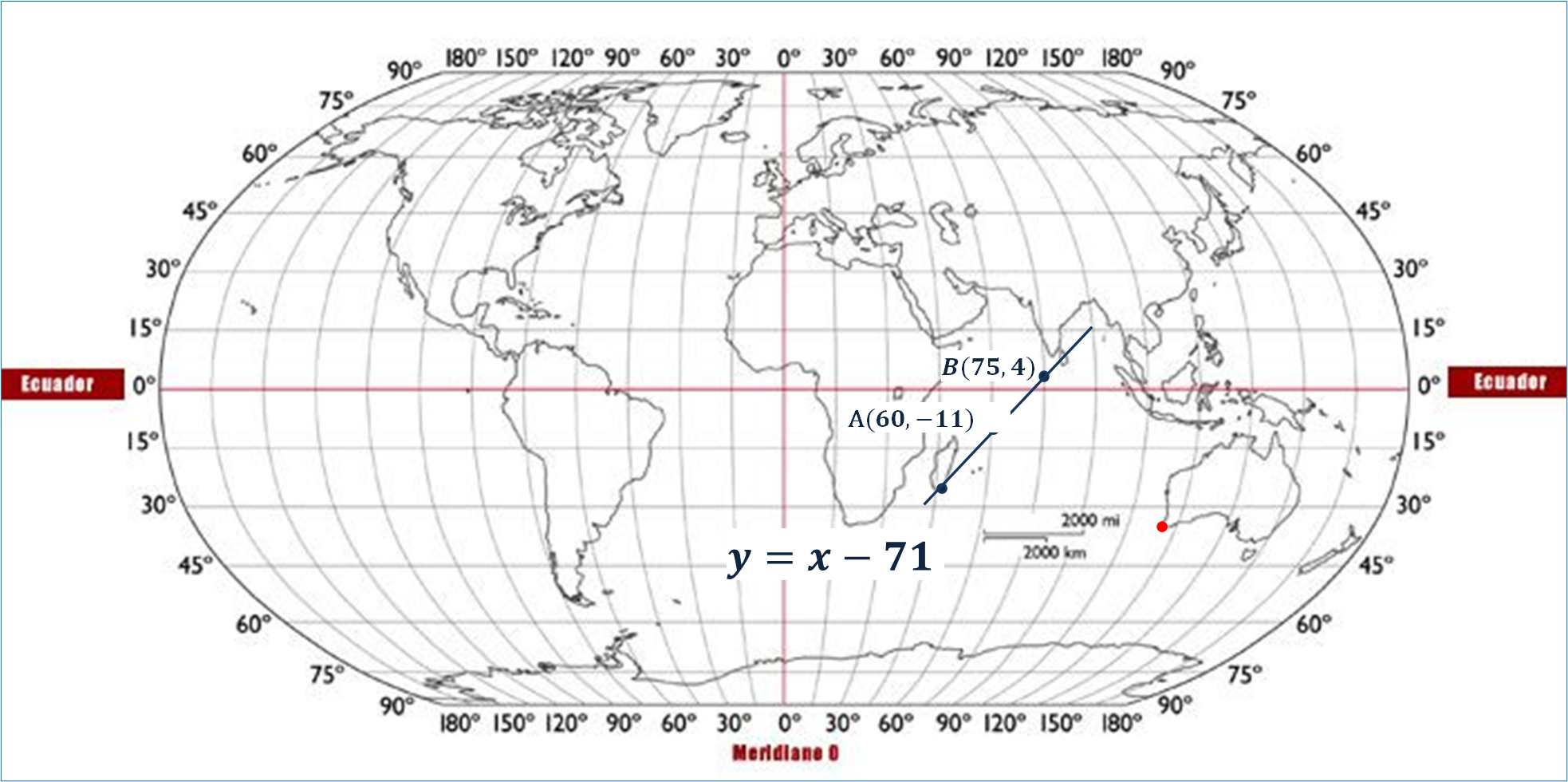
Ahora, analiza el sistema de ecuaciones en la gráfica y responde: las rectas, ¿se encuentran entre sí? ¿qué significa esto?

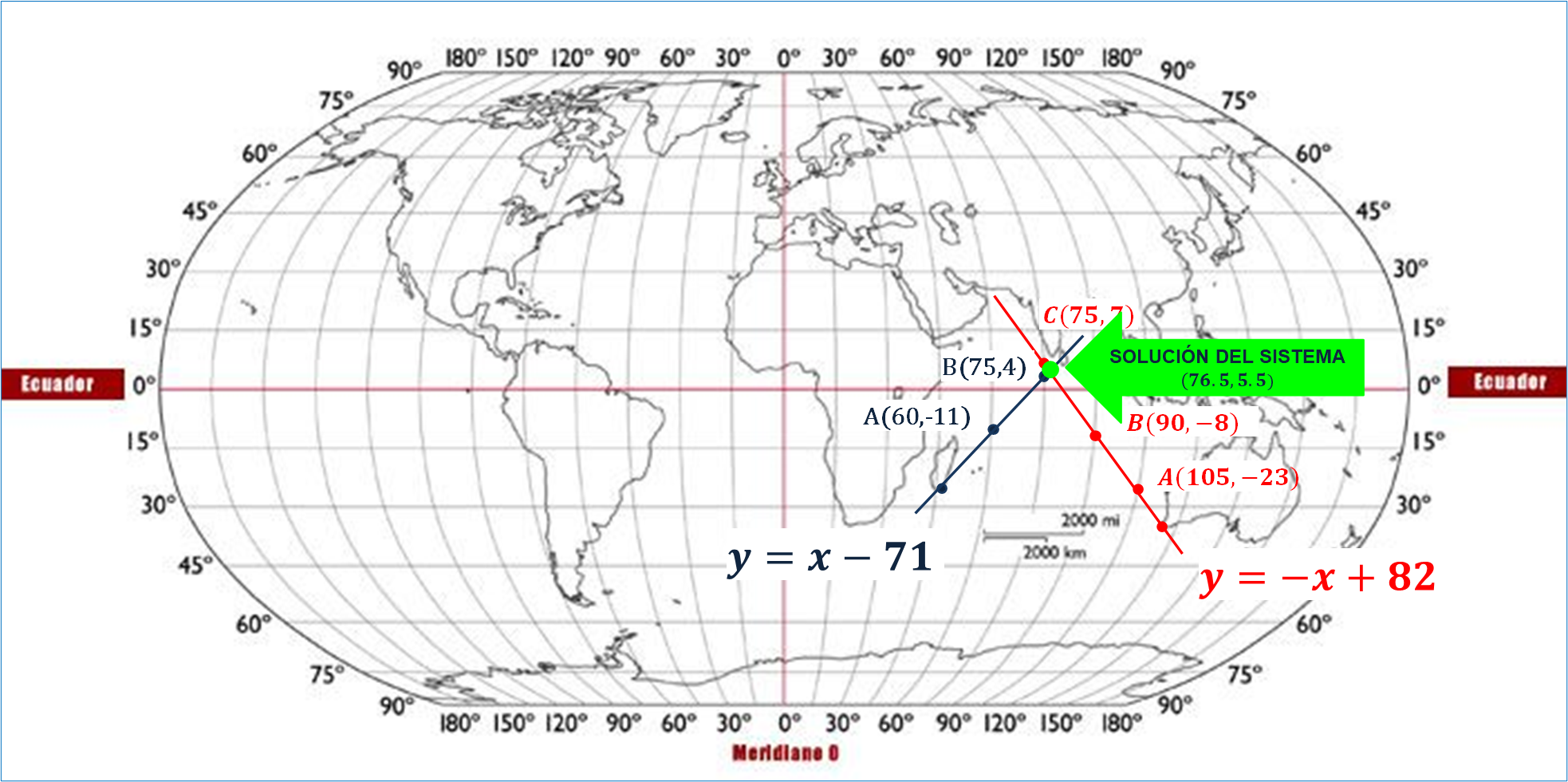
En la gráfica, se puede observar que hay un punto de intersección entre las líneas rectas obtenidas de las ecuaciones lineales con dos incógnitas del sistema, por lo tanto, se afirma que el sistema tiene una única solución, es decir, que en este sistema de ecuaciones si se encuentran los barcos 1 y 2 en las coordenadas (76.5, 5.5)

En esta sesión identificaste el proceso de resolución de un sistema de ecuaciones lineales (2 por 2), mediante el método gráfico, el cual consiste en:

1. Plantear el Sistema de Ecuaciones Lineales 2 por 2
2. Despejar la incógnita “y” en ambas ecuaciones.
3. Asignar valores a la literal “x” y sustituirlos en los correspondientes despejes de “y”.
4. Elaborar en un mismo plano cartesiano la gráfica de cada ecuación que forma el sistema.
5. Interpretar la gráfica resultante para identificar la solución del sistema y con ello la solución del problema.

Has finalizado esta sesión. Se deseas saber más del tema, puedes consultar tu libro de texto de Matemáticas.

El reto de hoy:

Consulta tu libro de texto de Matemáticas de segundo grado, en el tema correspondiente, y resuelve los problemas que encuentres mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas, utilizando el método gráfico.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/