Problemas de suma y resta con números positivos y negativos

Problemas de suma y resta con números positivos y negativos

Aprendizaje esperado: resuelve problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos.

Énfasis: resolver problemas aditivos que involucran números enteros, fracciones y números decimales positivos y negativos.

¿Qué vamos a aprender?

Hoy trabajarás en la resolución de problemas aditivos, que implican el uso de números enteros, fracciones y números decimales positivos y negativos, aplicados en distintos contextos.

¿Qué hacemos?

Para iniciar revisa la siguiente situación. Pon atención y ve tomando nota de la información más relevante.

Mario asistió a ver a un nutriólogo para iniciar un tratamiento de control de peso, ya que su médico familiar le recomendó cambiar sus hábitos alimenticios; además, le recomendó realizar alguna actividad física por 30 minutos diarios. El nutriólogo le sugirió realizar algunos ejercicios en casa para mejorar su salud. Mario se propuso bajar 10 kilogramos en 6 meses, para ello realizó la siguiente tabla donde registró cómo varía su masa corporal cada mes.

El planteamiento requiere de saber cuántos kilogramos logró bajar Mario durante estos 6 meses.

Para ello, se te sugiere anotar la siguiente tabla en tu cuaderno o, en su defecto, en hojas reutilizables.

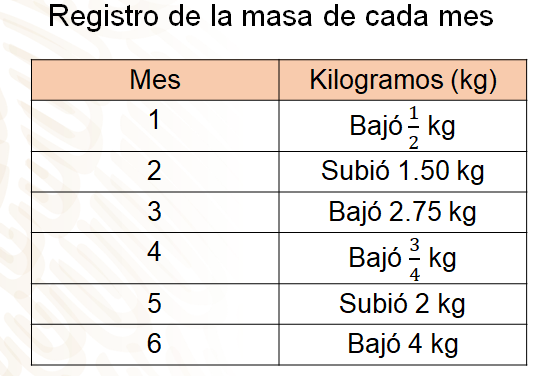
Esta es la tabla que realizó Mario para llevar su control de masa corporal mes con mes. En la primera columna escribió el “Mes”, en la segunda columna “Kilogramos”, donde registró cuánto subió y cuánto bajó. Esta información se puede comprender como la pérdida o ganancia de peso que tuvo cada mes.

En los registros, en el primer mes Mario bajó medio kilogramo; en el segundo mes, subió 1.50 kilogramos; en el número “3” bajó 2.75 kilogramos; para el cuarto mes bajó tres cuartos de kilogramo, en el quinto mes subió 2 kilogramos y en el sexto mes bajó 4 kilogramos.

Después de leer el planteamiento, se te sugiere anotar en tu cuaderno las siguientes preguntas para reflexionar:

• ¿Qué operaciones serán necesarias para solucionar el problema?
• ¿Cuántos kilogramos perdió Mario durante estos seis meses?
• ¿Logró bajar los 10 kilogramos que se propuso?

Ahora se dará respuesta a la primera interrogante. Toma nota para responder a las preguntas que surgieron en este problema.

Para la pregunta: ¿Qué operaciones serán necesarias para solucionar el problema?

Primero se debe analizar los datos de la tabla mes con mes para ver lo que sucedió.

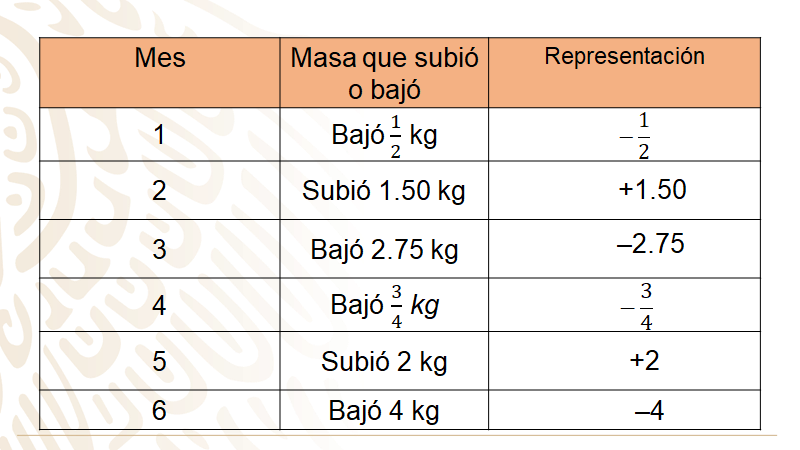
En el primer mes perdió medio kilogramo, así que se puede representar con números negativos. En el segundo mes subió o incrementó 1.50 kilogramos, por lo tanto, se representará con un número positivo; en el tercer mes bajó 2.75 kilogramos, ¿qué tipo de número representaría lo anterior?

En este caso un número negativo: 2.75 negativo; y en el cuarto mes se debe asociar tres cuartos de kilogramo con un número negativo; en el quinto mes Mario subió 2 kilogramos, por lo que se representa con un número positivo y en el último mes perdió 4 kilogramos, lo cual se representa con 4 negativo.

Entonces es necesario resolver una adición de números positivos y negativos para saber cuánta masa perdió o ganó en los 6 meses que duró su tratamiento.

Para ello se plantea la siguiente operación en forma horizontal: menos un medio, más 1.50, más 2.75 negativo, más tres cuartos negativos, más 2, más 4 negativo.

Con la operación ya establecida, se puede dar respuesta a la segunda pregunta, que es: ¿Cuántos kilogramos perdió Mario durante estos seis meses de tratamiento?

Para dar solución a la operación menos un medio, más 1.50 más 2.75 negativo, más tres cuartos negativos, más 2, más 4 negativo, se aplicará la propiedad asociativa; es decir, primero debes agrupar o sumar por separado los números positivos y negativos para después resolver la operación con los valores resultantes.

De color rojo se señalan los números negativos: un medio negativo, 2.75 negativo, tres cuartos negativos y 4 negativo; y de color azul los números positivos: 1.50 y 2. Es importante recordar que en los números positivos se omite el signo “más”, de modo que los signos que aparecen son los signos de la operación, por eso no se señalan con azul.

Ya que se tienen agrupados los números negativos y los positivos, se resuelven las operaciones. ¿Recuerdas cómo sumar números negativos y positivos?

Como sabes, la regla de la adición de números positivos y negativos indica que, al sumar números del mismo signo, se suman los valores absolutos y el resultado conserva el signo de los sumandos correspondientes.

Para facilitar la suma en el caso de los números negativos, se convierten las fracciones a número decimal. Para ello, se divide el numerador entre el denominador: 1 entre 2 es igual a 0.5, un medio negativo es igual a 0.5 negativo. Ahora se convierte la fracción tres cuartos a número decimal, para ello sólo se divide 3 entre 4 que da como resultado 0.75; 3/4 negativos son igual a 0.75 negativo. Ya se puede resolver la suma de números negativos: 0.5 negativo más 2.75 negativo, más 0.75 negativo más 4 negativo es igual a 8 negativo. La segunda suma 1.50 más 2 da como resultado 3.50 positivo.

Finalmente, se suman los resultados obtenidos. Para resolver esta operación se utiliza la regla de la adición de un número positivo y uno negativo: se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto: 8 menos 3.50 es igual a 4.50 y como 8 negativo tiene mayor valor absoluto que 3.50, el resultado es negativo. Por lo tanto, 8 negativo más 3.50 es igual a 4.50 negativo.

Como pudiste ver, el resultado es 4.50 negativo, que en este caso significa que Mario, durante estos seis meses, bajó 4.50 kilogramos.

Dando respuesta a la tercera pregunta que dice: ¿Mario logró bajar los 10 kilogramos que se propuso?

Desafortunadamente no lo logró, pero ¿cuántos kilogramos le faltaron para lograr su objetivo?

Si respondiste que le faltaron 5.50 kilogramos, tu respuesta es correcta.

¿Cuántos kilogramos pesa Mario, si antes de empezar a realizar estos cambios, su masa era 68.4 kilogramos?

Para encontrar su masa actual, ¿qué operación se debe realizar?

La respuesta es, una sustracción, a su masa inicial que era 68.4 kilogramos se tiene que sumar lo que bajó durante estos seis meses, que fueron 4.5 kilogramos; es decir, 4.5 negativo. Como lo viste antes, se calcula la diferencia entre 68.4 menos 4.5 igual a 63.9, por lo que la masa de Mario al final del tratamiento era de 63.9 kilogramos.

Siguiendo con el tema de estudio ahora se analizará otra situación, relacionada con José, un joven que juega futbol americano.

El futbol americano es un juego que consiste en que cada equipo tiene que lograr, en 4 jugadas, avanzar 10 yardas para tener otras 4 oportunidades de seguir avanzado y así llegar hasta la zona de anotación del equipo contrario para ganar 6 puntos. Si en cuatro oportunidades no avanza 10 yardas entrega el balón al equipo contrario. Ahora que ya sabes de forma muy general en qué consiste el juego, revisa algo que le pasó a José.

José juega como corredor. Su responsabilidad es correr la mayor cantidad de yardas posibles para ayudar a su equipo a realizar una anotación, pero también puede perder yardas debido a que la defensiva del equipo contrario puede hacerlo retroceder.

Antes de continuar, tal vez te estarás preguntando ¿qué es una yarda?

La yarda es una unidad de medida del Sistema Inglés y equivale a 91.44 cm. Estudiarás ésta y otras unidades de longitud en segundo grado de secundaria.

Por ahora, se te pregunta: ¿José habrá logrado juntar las 10 yardas que necesita su equipo para obtener otras 4 oportunidades de seguir avanzando?

Para dar respuesta a esta pregunta, se te sugiere copiar la siguiente tabla:

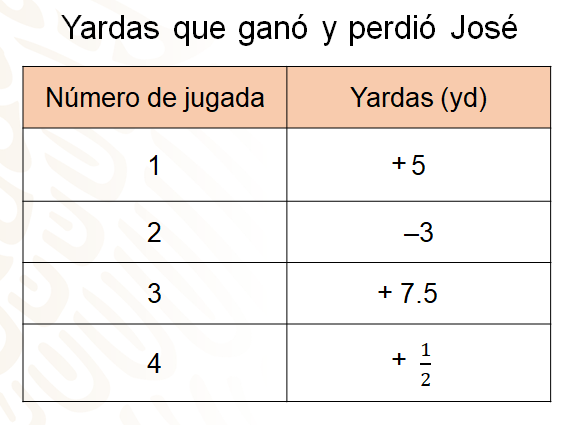
Esto es lo que sucedió con las yardas que ganó y perdió José en sus cuatro oportunidades. En la primera columna se encuentra el número de las jugadas, en la segunda columna las yardas que ganó o perdió en cada oportunidad. En la primera ganó 5 yardas, que se puede representar con un número positivo. Como en la segunda jugada perdió 3 yardas, se representa con un número negativo, en la tercera jugada ganó 7.5 yardas y en la cuarta jugada ganó media yarda.

Con esta información se puede dar respuesta a la pregunta, ¿en qué yarda quedó el equipo de José después de su cuarta corrida?

Ya que la tabla anterior facilita establecer las operaciones que se deben realizar, se hará una adición de las yardas que ganó y que perdió José.

Al igual que en el caso anterior, se coloca la operación en forma horizontal: 5 positivo, más 3 negativo, más siete punto cinco positivo, más un medio positivo.

Para resolver la operación, primero se convierte un medio a número decimal. Para ello debes dividir el numerador entre el denominador, por lo que al dividir 1 entre 2 es igual a 0.5. Ahora ya tienes lista la operación para darle solución: + 5 + (–3) + 7.5 + 0.5, aplicas la propiedad asociativa, agrupando los números positivos, que son 5, 7.5 y 0.5, por lo que se suma, dando como resultado 13 positivo. Ahora, sumas el resultado anterior con el único número negativo, que es 3 negativo.

¿Qué procedimiento tiene que seguirse para sumar dos números con signos diferentes?

La respuesta es que se calcula la diferencia entre los valores absolutos.

¿Cuál es el número de mayor valor absoluto?

El número 13, por lo tanto, el resultado será un número positivo, al aplicar la sustracción 13 menos 3 da 10; por lo tanto, 13 más 3 negativo es igual a 10 positivo.

Al resolver la operación dio 10 positivo, lo que significa que José ayudó a que su equipo tuviera otras 4 oportunidades para lograr una anotación.

¿A qué yarda llegó José de su posición inicial, que era la yarda 25?

José llegó a la yarda 35.

Bien, ahora qué te parece si se analiza la segunda oportunidad que tuvo el equipo de José para observar cuál fue su desempeño.

En la siguiente imagen podrás observar lo que sucedió con las yardas que ganó y perdió José en su segunda oportunidad, para intentar realizar una anotación.

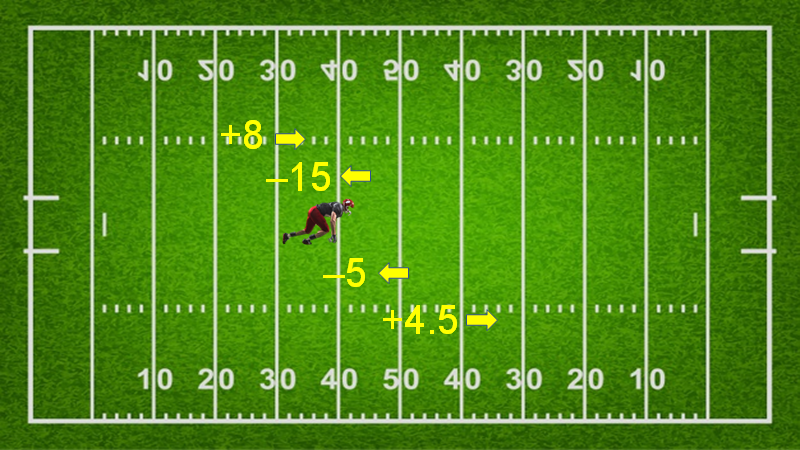
En la primera ganó 8 yardas, en la segunda jugada uno de sus compañeros cometió una falta y perdieron 15 yardas; por lo tanto, se representa con un número negativo. En la tercera jugada recibieron otro castigo, por lo cual perdieron 5 yardas más. ¿Con qué tipo de número se puede representar lo anterior?

Con un número negativo. En la cuarta jugada José ganó 4.5 yardas.

Pero ¿José y su equipo habrán logrado las 10 yardas que necesitan para seguir avanzando?

Para conocer la respuesta se coloca la operación en forma horizontal: 8 positivo, más 15 negativo, más 5 negativo, más 4.5 positivo. Se suman por separado los números positivos y los negativos: 8 más 4.5 es igual a 12.5. Ahora, se hace lo mismo con los números negativos: 15 negativo, más 5 negativo es igual a 20 negativo. Al sumar los resultados obtenidos, que son 12.5 positivo y 20 negativo, se calcula la diferencia de los valores absolutos: 20 menos 12.5 igual a 7.5. ¿Cuál es el número de mayor valor absoluto?

20 negativo, por lo que el resultado es un número negativo; así 12.5 más 20 negativo es igual a 7.5 negativo.

Al resolver las operaciones te puedes dar cuenta de que, desafortunadamente, en esta ocasión el equipo de José no logró juntar las 10 yardas que necesitaba para seguir avanzando.

Pero ¿qué significa obtener, en este caso, un resultado negativo?

Que el equipo de José perdió 7.5 yardas. Si en su segunda oportunidad iniciaron en la yarda 35, después de estas cuatro oportunidades quedaron en la yarda 27.5.

Ahora revisa otra situación en la que el protagonista es Martín. Él trabaja en una empresa donde realizan cajas de ahorro, con la finalidad de fomentar el hábito del ahorro entre los trabajadores. Cada persona ahorra mensualmente la cantidad que quiera y también se les otorgan préstamos con intereses muy bajos de sus mismos ahorros. Durante los primeros 8 meses ahorró cierta cantidad y también pidió tres préstamos. Para llevar un control, el registro que lleva de sus ahorros y préstamos los organiza en una tabla, como la que se muestra a continuación. Toma nota de la siguiente información.

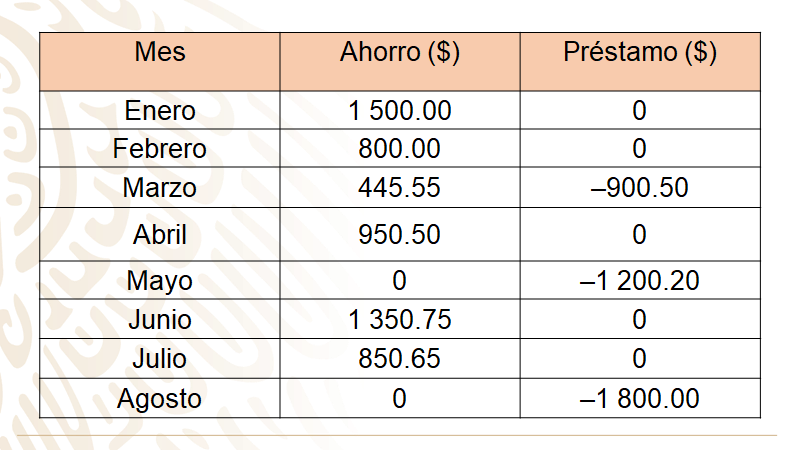
En la primera columna escribió el “Mes”, en la segunda columna las cantidades que ahorró y en la tercera columna las cantidades que pidió prestadas.

Como puedes ver, en enero ahorró $1,500, y en este mes no pidió ningún préstamo; en el mes de febrero ahorró $800 y no pidió préstamos; en marzo ahorró $445.55 y pidió un préstamo de $900.50, el cual se representa con números negativos, por ser un egreso a sus ahorros. En el cuarto mes, abril, ahorró $950.50; en mayo no ahorró, pero pidió un préstamo de $1,200.20; en junio su ahorró fue de $1,350.75, sin préstamos solicitados; en julio ahorró $850.65 y en agosto tampoco ahorró y solicitó un préstamo de $1,800.

Ahora revisa las siguientes preguntas:

• ¿Cuánto dinero lleva ahorrado durante estos 8 meses?
• ¿Cuánto dinero pidió prestado?

Si en los siguientes cuatro meses del año ahorró $950 y pidió un préstamo de $325.50, ¿cuánto dinero tendrá ahorrado al final del año?

Como viste en los ejemplos anteriores, con una adición de números positivos y negativos se pueden representar los ahorros. Con esto ya se puede organizar la operación que se utilizará para dar respuesta a la primera pregunta: ¿cuánto lleva ahorrado durante estos 8 meses?

La operación es la siguiente:

1500 + 800 + 445.55 + (–900.50) + 950.50 + (–1200.20) + 1350.75 + 850.65 + (–1800).

Para dar solución, se aplica la propiedad asociativa, se agrupan los números positivos, que son 1500 + 800 + 445.55 + 950.50 + 1350.75 + 850.65 y da como resultado 5,897.45 pesos. Ahora, se realiza el mismo procedimiento para los préstamos: (–900.50) + (–1200.20) + (–1800) = –3,900.70.

¿Qué operación se efectúa ahora?

Se calcula la diferencia entre los valores absolutos de 5,897.45 y 3,900.70 negativo, dando como resultado 1,996.75. De 5,897.45 y 3,900.70 negativo, ¿cuál tiene el mayor valor absoluto?

5,897.45, por lo tanto, el resultado será positivo; es decir que Martín tenía ahorrados, hasta agosto, 1,996.75 pesos.

¿Cuánto dinero tenía ahorrado Martín al final del año?

Considera que, durante los últimos cuatro meses del año ahorró $950 y pidió un préstamo de 325.50 pesos.

En casa ¿ya tienes la respuesta?

La respuesta es que Martín ahorró 950 pesos y pidió 325.50 pesos, entonces en esos meses ahorró 624.50 pesos, más los 1,996.75 pesos que ya había ahorrado antes, hacen un total de 2,621.25 pesos.

Bien, se han resuelto problemas aditivos, en donde se implica el uso de números enteros, fracciones y números decimales positivos y negativos. Como pudiste ver, este tipo de números están presentes en muchas situaciones cotidianas.

Sabes que, al sumar números con signos iguales, se suman los valores absolutos y el resultado tendrá el mismo signo de los sumandos; si se suman números con diferente signo, se calcula la diferencia de los valores absolutos y el resultado tendrá el signo del número con mayor valor absoluto.

¿Qué te parece si ahora revisas un problema relacionado con la sustracción de números positivos y negativos?

Monterrey, en el estado de Nuevo León, es una ciudad con un clima muy extremo: la temperatura puede cambiar mucho en un mismo día. Cierto día de invierno, en la madrugada, la temperatura era de 3.4 grados Celsius bajo cero y durante la tarde del mismo día llegó a 23.5 grados Celsius.

¿Cómo puedes calcular la variación de la temperatura en ese día?

Como lo que se quiere saber es la diferencia entre las temperaturas; es decir, cuánto le falta a 3.4 negativo para llegar a 23.5, lo que se tiene que realizar es una sustracción.

Revisa la siguiente imagen:

Para saber lo que le falta a 3.4 negativo para llegar a 23.5; es decir, para establecer cómo varió la temperatura, se resuelve la resta 23.5 menos 3.4 negativo; y, como sabes que restar es lo mismo que sumar por el inverso aditivo, entonces 23.5 menos 3.4 negativo es igual a 23.5 más 3.4 positivo, que es igual a 26.9. Lo que significa que la temperatura aumentó 26.9 grados.

Lo anterior se pude justificar con el apoyo de la recta numérica. Para llegar de 3.4 negativo a 23.5 se tiene que mover hacia la derecha, primero 3.4 unidades para llegar al cero y posteriormente, 23.5 unidades. Al sumar estos dos valores 3.4 más 23.5 el resultado es 26.9 y, como se movió hacia la derecha, el resultado es positivo.

Sin duda, la recta numérica resulta de gran ayuda para entender y justificar la sustracción de un número negativo.

Bien has concluido el tema del día de hoy. Si quieres saber más sobre el tema revisa tu libro de texto y realiza las actividades que ahí se sugieren. De igual manera puedes consultarlo con tu profesora o profesor de esta asignatura.

El reto de hoy:

Se propone que calcules del último ejercicio realizado en la sesión, cuánto le falta a 18.4 para llegar a 1.8 negativo. Asimismo, que des respuesta a las siguientes preguntas:

• ¿Qué operación permite obtener el resultado?
• ¿El resultado será un número positivo o negativo?

Para validar tus respuestas representa la situación en una recta numérica.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html