Atletismo

Atletismo

Aprendizaje esperado: aplicar un factor constante de proporcionalidad (entero y pequeño) para obtener valores faltantes en una relación de proporcionalidad con magnitudes de la misma naturaleza.

Énfasis: identificar el factor constante de proporcionalidad al completar una tabla de ahorro.

¿Qué vamos a aprender?

Identificarás el factor constante de proporcionalidad al completar una tabla de ahorro.

¿Qué hacemos?

En la sesión de hoy continuaremos revisando el factor constante de proporcionalidad, vamos a comenzar la clase leyendo una de las tantas cartas que recibimos semanalmente. Escogí la carta de Gerardo, porque está relacionada con el tema que nos ocupa: elaborar tablas con ayuda del factor constante de proporcionalidad. Además, Gerardo pide nuestra ayuda. Te invito a leer su carta para saber de qué manera le podemos apoyar. La carta dice así:

8 de febrero de 2021

Querida maestra Andrea. Todos los días la veo desde mi casa. Quiero decirle que me encantan sus clases y que he aprendido mucho con usted. Me presento: mi nombre es Gerardo Rentería Canseco y voy en 5º grado.

Le cuento que cerca de mi casa está la unidad deportiva del municipio. A mí me gusta mucho ir a correr en la pista y ahora, por la pandemia, estoy yendo a entrenar, pero respetando días y horarios. Hace poco, mi tío Pepe que es el entrenador, me pidió ser su asistente.

En estos tiempos, le ayudo a elaborar tablas donde los corredores registran sus tiempos y las distancias con las que trabajan. Como todos tienen diferentes rendimientos, mi tío me pide elaborar tablas para que los corredores sepan en qué distancia deben trabajar ciertos ejercicios. La tabla que me pidió elaborar para la siguiente semana consiste en triplicar la distancia con la que trabajaron en esta semana.

Me gustaría pedirles su ayuda para estar seguro de mis cálculos. De antemano, muchas gracias.

Atentamente,

Gerardo

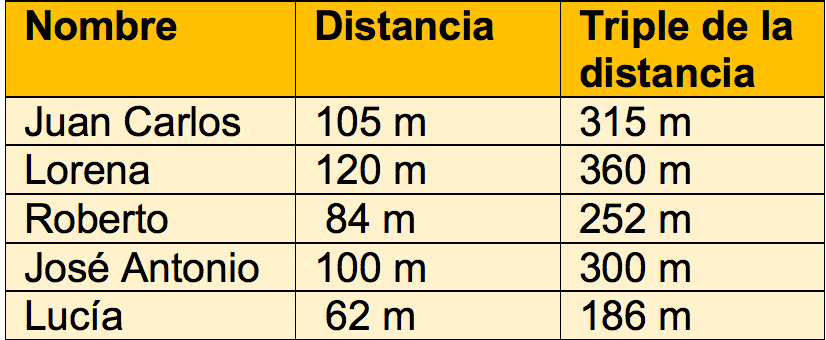
Aquí está la tabla que Gerardo tiene que resolver.

Esta tabla es muy parecida a las tablas que elaboraste la clase pasada. Solo que en lugar del doble o cuádruple de una cantidad, ahora debes de obtener el triple. Si queremos obtener el triple de la distancia de cada corredor, lo que debes hacer es multiplicarla por el factor constante de proporcionalidad, que en este caso es tres.

Imagina que tienes la distancia AB, y que mide 10 metros. Observa la siguiente figura:

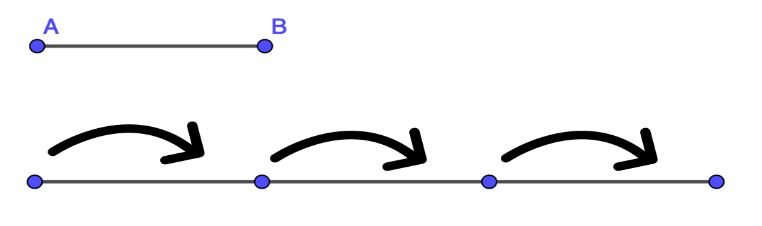
Para obtener el triple de la distancia original necesitas repetir esa distancia tres veces. Entonces la distancia triplicada sería 30 metros.

¿Qué te parece si le ayudas a Gerardo a hacer los cálculos? Llena la tabla.

105 se puede descomponer en 100 y 5 entonces tres veces 100 es 300. Tres veces cinco es 15 ahora, si sumas 300 más 15 te da 315.

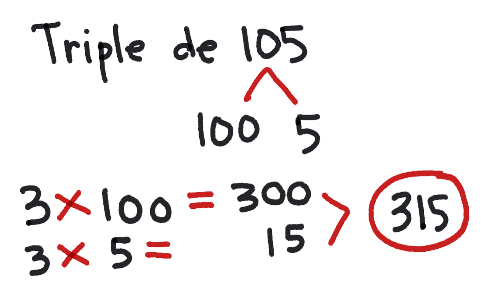
120 se puede desagrupar en 100 y 20. Tres veces 100 es igual a 300. Tres veces 20 son 60 entonces 300 más 60 son 360.

En el caso de 84 se puede descomponer en 80 y 4. Para obtener el triple de 80 es como si multiplicaras 3 veces 8, lo que da 24, pero debes agregar un cero porque no son 8, sino 80; así que son 240. El triple de 4 es 12. Si sumas 240 más 12 te da 252.

La siguiente es el triple de 100 es 300.

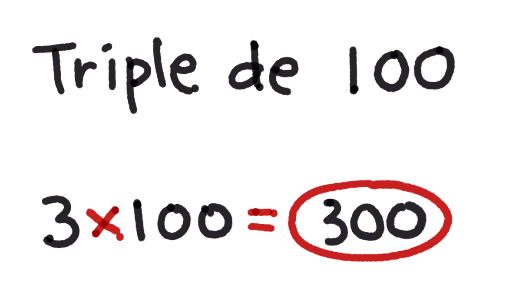
Con respecto al 62, se puede desagrupar en 60 y 2. El triple de 60 es 180 porque 3 veces 6 es 18 pero deberás agregar un cero porque no es 6, son 60. El triple de 2 es 6 entonces al sumar 180 más 6 tenemos 186.

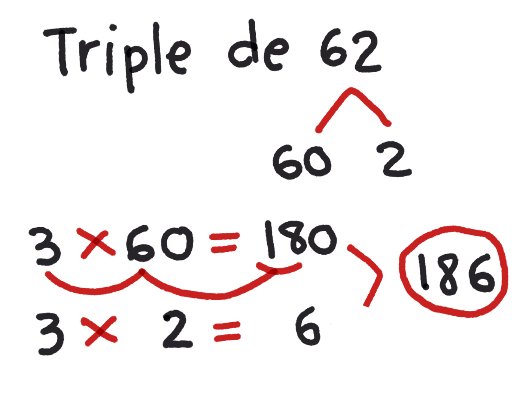
Así quedó la tabla. Gerardo va a estar muy contento porque los resultados obtenidos justamente son los mismos resultados que él calculó.

Ahora el entrenador Pepe le pide a Gerardo que calcule la distancia original a partir de darle la distancia triplicada, ¿Qué debería hacer Gerardo?

Vamos a suponer que el triple de la distancia es 375. ¿Cuál sería la distancia original?

Como ya sabemos que tres es el factor constante de proporcionalidad, entonces divide la distancia triplicada entre tres para obtener la distancia original. Divide 375 entre 3.

El resultado es 125. Eso quiere decir que la distancia antes de triplicarla sería 125.

Para poner a prueba tu comprensión del tema, te pido ahora abras tu libro de Desafíos Matemáticos en las páginas 73 y 74 para que resuelvas el Desafío número 33: El ahorro.

Revisa de qué se trata.

Consigna: En equipos resuelvan el siguiente problema y luego contesten las preguntas.

El Sr. Laurentino quiere fomentar en su hijo Diego el hábito del ahorro; para ello le propuso que cada semana le daría el doble de la cantidad de dinero que pudiera guardar. En la siguiente tabla aparecen varias cantidades ahorradas por Diego, calculen las cantidades dadas por su papá y complétenla.

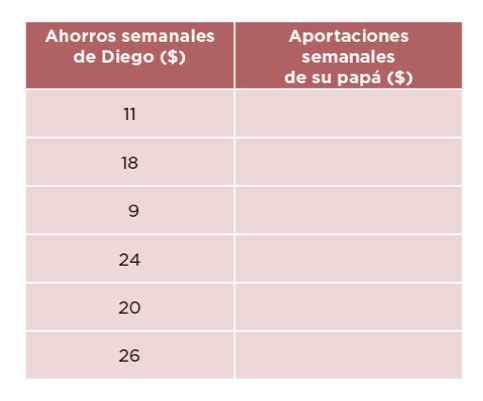
Se parece mucho a las tablas que ya estuviste trabajando.

• El doble de 11 es dos veces 11 (2X11). Esto es igual a 22.
• El doble de 18 es dos veces 18 (2X18). El resultado es 36.
• El doble de 9 es dos veces 9 (2X9). Esto es igual a 18.
• El doble de 24 es dos veces 24 (2X24). Esto es igual a 48
• El doble de 20 es dos veces 20 (2X20). El resultado es 40.
• El doble de 26 es dos veces 26 (2X26). Esto es igual a 52.

Así te debe quedar la tabla:

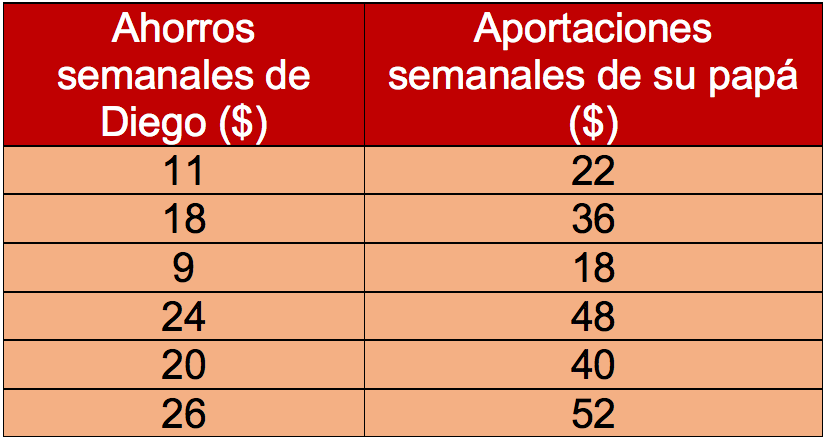
Hay que poner a prueba tu comprensión del tema. ¿Listo?

¿Qué relación hay entre el dinero que aporta el Sr. Laurentino y el dinero que ahorra su hijo?

R = La cantidad que aporta el Sr. Laurentino es dos veces la cantidad que ahorró Diego, es decir, la relación que existe entre ambas cantidades es el doble.

¿Qué operación realizaste para encontrar los valores de la segunda columna?

R = Si te fijaste bien, todas las cantidades de la tabla están multiplicadas por dos. Eso quiere decir que dos es el factor constante de proporcionalidad.

¿Cuánto tiene que aportar el papá si Diego ahorra $35?

R = Tiene que ser lo doble de 35. Dos veces 35 (2X35). Da como resultado 70.

En una ocasión el papá le dio a su hijo $146. ¿Cuánto ahorró Diego?

R = Esto da $73.

Si te fijaste bien, la cantidad esta duplicada. Esto quiere decir que, si se divide entre 2, el factor constante de proporcionalidad, podrás saber cuánto ahorró Diego. Debes dividir 146/2.

Aquí el proceso es inverso: En lugar de multiplicar por dos, se divide entre dos.

En otra ocasión el papá le dio $3. ¿Cuánto ahorró Diego?

R = Si divides 3/2 obtendrás $1.50.

Con lo que hemos visto la clase pasada y hoy, lo pudiste resolver sin ninguna dificultad.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/