Sumas y restas de fracciones positivas y negativas

Sumas y restas de fracciones positivas y negativas

Aprendizaje esperado: resuelve problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos.

Énfasis: resolver problemas aditivos con fracciones positivas y negativas.

¿Qué vamos a aprender?

Durante el desarrollo de esta lección resolverás problemas de suma y resta con números decimales y fracciones positivas y negativas.

¿En qué situaciones se emplean la suma de números decimales o fracciones?

¿Qué hacemos?

Lee la siguiente situación:

Eduardo tiene un negocio y diariamente, al final del día, realiza una comparación entre los egresos (dinero que sale del negocio) y los ingresos (dinero que entra al negocio) para obtener el balance y así tener un control de sus ganancias.

Analiza la siguiente imagen que muestra una tabla:

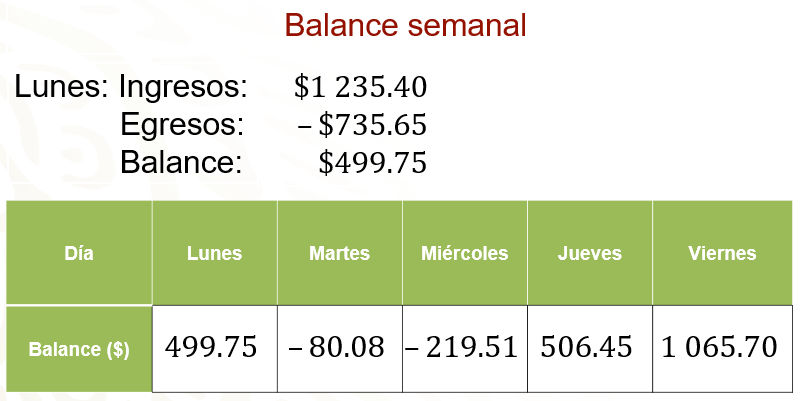
La tabla muestra el balance durante una semana de trabajo de Eduardo. Por ejemplo, en el caso del lunes, los ingresos del negocio fueron de 1,235.40 pesos y los egresos de 735.65 pesos, cantidad que se representa con números negativos por representar en este caso una perdida. Al hacer el balance entre los ingresos y egresos de ese día, el resultado fue de 499.75 pesos, lo que representa las ganancias de ese día para Eduardo. Después de realizar el cálculo anterior para los siguientes días, los resultados fueron que: el día martes obtuvo 80.08 pesos negativos, el miércoles el balance fue de 219.51 pesos negativos, el jueves fue de 506.45 pesos y el viernes de 1,065.70 pesos.

Te puedes dar cuenta que, durante dos días de la semana, el martes y el miércoles Eduardo tuvo pérdidas en su negocio, lo que significa que esos días los egresos fueron mayores a los ingresos que obtuvo.

Pero lo importante será hacer el balance semanal para verificar si los ingresos superaron a los egresos y así tener un panorama general y poder determinar si Eduardo tuvo ganancias o pérdidas durante esa semana.

¿Qué procedimiento tienes que seguir para calcular el balance semanal de Eduardo? ¿Cuál es el balance?

Lo que tienes que hacer en este caso es una adición de números positivos y negativos.

Antes de resolver la operación, recuerda las reglas de la adición de números positivos y negativos que también aplican para los números decimales y para las fracciones.

Al sumar dos números con el mismo signo, se suman los valores absolutos y el resultado conserva el mismo signo de los sumandos.

Al sumar dos números con diferente signo, se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.

Primero suma por separado las cantidades positivas y negativas. Alinea las cantidades con el punto decimal y suma de derecha a izquierda, tal como lo muestra la siguiente imagen;

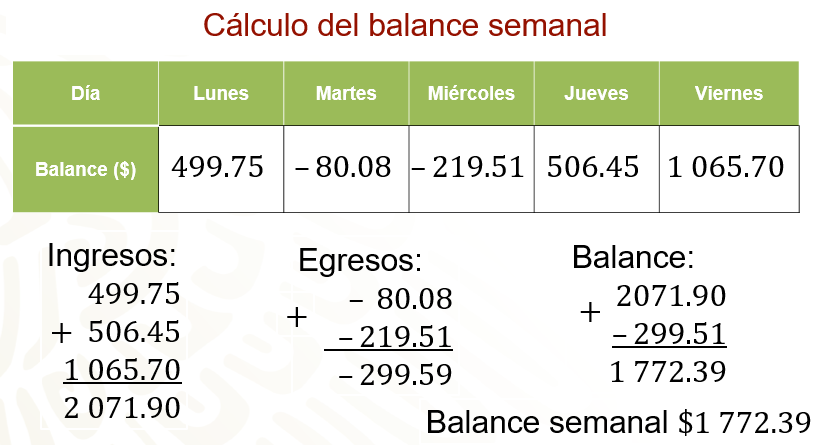
Suma 499.75 más 506.45 más 1065.70 que es igual a 2,071.90. Ahora sumamos los números negativos: 80.08 negativo más 219.51 negativo es igual a 299.59 negativo. Ahora suma los resultados anteriores: 2,071.90 más 299.59 negativo es igual a 1,772.39. Con este resultado ya sabes que el balance semanal de Eduardo fue de 1,772.39 pesos.

En situaciones como la anterior puedes identificar la importancia de saber operar con números positivos y negativos.

Ahora te invito a que calculemos cuál es la diferencia entre el día con mayores ingresos y el día de mayores egresos.

El orden de menor a mayor de las cantidades lo puedes ver en la siguiente tabla:

La cantidad menor, que corresponde al miércoles y es 2,19.51 negativo, después, 80.08 negativo, 499.75, 506.45 y 1,065.70.

Esto quiere decir que, 219.51 es menor que 80.08 negativo, y éste a su vez es menor que 499.75, que también es menor que 506.45, que a su vez es menor que 1,065.70.

Esto quiere decir que la cantidad menor de estos registros es 219.51 negativo y la mayor es 1,065.70.

Ya que conoces el orden de las cantidades, se calcula la diferencia entre el número menor y es mayor, es decir, entre la máxima perdida de Eduardo y la mayor ganancia.

Reflexiona: ¿Qué operación realizarás, una suma o una resta?

La operación que tienes que hacer es una resta, porque se pretende encontrar una diferencia.

La diferencia es igual a cantidad mayor menos cantidad menor, que en este caso es 1,065.70 menos 219.51 negativo.

Antes de resolver la operación, recuerda utilizar los paréntesis para no confundir la operación de sustracción con el carácter positivo o negativo de los números.

¿Cómo son los números que estas restando?

Estas restando un número negativo de un número positivo.

Entonces la estructura es una resta entre un número positivo y uno negativo.

Por ejemplo, resuelve la siguiente operación: 20 – (–72)

En esta ocasión utilizaremos al inverso aditivo para resolver la sustracción:

Ya sabes que el inverso aditivo de un número entero es su simétrico, de tal forma que al sumar un número entero con su simétrico, la suma que se obtiene es cero.

Utiliza esta propiedad para convertir una sustracción en adición:

Por ejemplo, “a” menos “b” es igual a “a” más el simétrico de “b”.

Así la operación 20 menos 72 negativo, la convertimos en 20 más 72, porque el simétrico de 72 negativo, es 72 positivo, y basta sumar 20 más 72 igual a 92.

Como lo muestra la siguiente imagen:

¿Qué significa esa diferencia de 92?

Esa diferencia significa que desde 72 negativo hasta 20 existen 92 unidades de distancia, esto lo puedes observar en la siguiente representación, utilizando a la recta numérica.

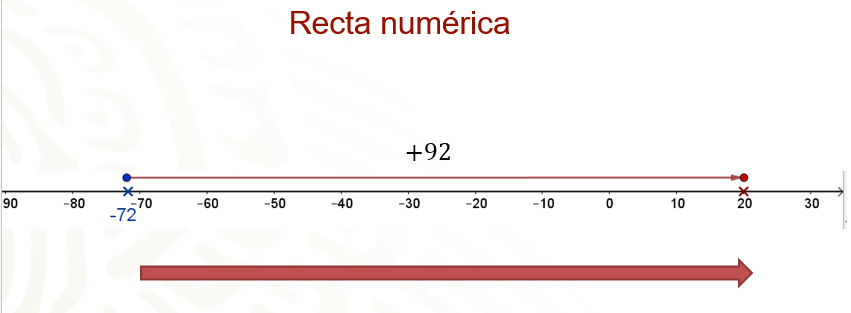
Al retomar el caso de Eduardo, para calcular la diferencia entre las cantidades, la resta 1,065.70 menos 219.51 negativo, ¿lo puedes representar y resolver como la suma: 1,065.70 más 219.51?

Efectivamente, porque 219.51 es el simétrico de 219.51 negativo.

Entonces la diferencia: 1,065.70 menos 219.51 negativo, es igual a 1,065.70 más 219.51 igual a 1 285.21.

Como lo muestra la siguiente imagen:

Así se sabe que la diferencia entre la máxima ganancia y la mayor pérdida fue de 1,285.21 pesos.

¿Qué pasaría si a la cantidad menor le restas la cantidad mayor?

Observa la siguiente explicación para aclarar la duda, retoma el caso de los números 72 negativo y 20 positivo.

En este caso, la diferencia es, a 72 negativo se le resta 20 positivo.

Ya sabes que una diferencia se puede convertir en adición, aplicando el inverso aditivo al sustraendo. Entonces, tenemos que 72 negativo menos 20 positivo es igual a 72 negativo más 20 negativo.

Resolviendo ahora esta operación, tenemos la suma de dos números negativos. Sumando 72 negativo más 20 negativo, el resultado es 92 negativo.

La primera regla de adición es: Al sumar dos números con el mismo signo, se suman los valores absolutos y el resultado conserva el mismo signo de los sumandos. En este caso, para sumar dos números negativos, se suman los valores absolutos y el resultado es un número negativo, tal como lo muestra la imagen:

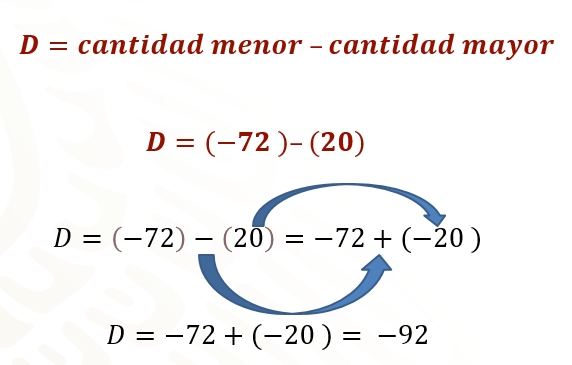
Pero ¿qué significado tiene este resultado?

Esto significa que, de 20 a 72 negativo hay 92 unidades negativas. Esto lo pueden visualizar con la siguiente recta numérica.

Observa que, en los dos casos anteriores, obtuviste como resultado a números simétricos.

Reflexiona:

¿Es lo mismo restar 20 menos 72 negativo que, restar 72 negativo menos 20 positivo?, observa la siguiente imagen:

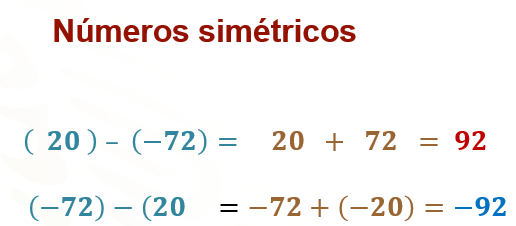
Como bien puedes observar no lo es, ya que la sustracción no cumple con la propiedad conmutativa. Además, el carácter positivo o negativo del resultado tiene un significado.

La primera operación, 20 menos 72 negativo cuyo resultado es 92, quiere decir que estamos comparando al 72 negativo con el 20 positivo; es decir, cuántos números hay desde el 72 negativo hasta el 20 positivo. Esto implica que, si a 72 negativo le sumamos 92 positivo, obtenemos 20 como resultado, como lo indica la imagen.

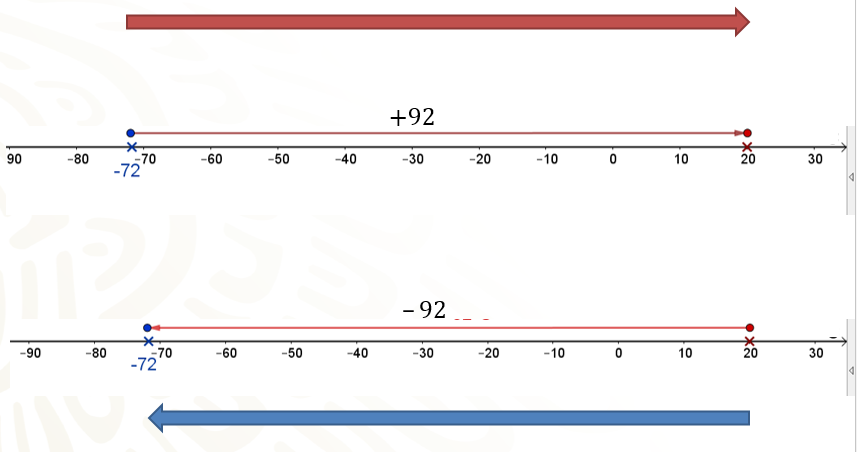
De manera análoga, en la segunda operación, 72 negativo menos 20 positivo, quiere decir que estamos comparando al 20 con el 72 negativo; es decir, cuántos números hay desde el veinte hasta el 72 negativo. Esto implica que, si a 20 le sumamos 92 negativo, obtenemos 72 negativo, como lo pueden apreciar en la imagen.

Entonces, ¿una sustracción se puede convertir en adición con ayuda del simétrico, o del inverso aditivo, aplicado al sustraendo?

Así es. Ya que realizaste una sustracción de números positivos y negativos.

Resuelve la siguiente situación. Toma nota de la información de la tabla y completa los datos que faltan.

La tabla presenta el balance semanal de los ingresos y egresos de Eduardo, se muestra el ingreso o egreso de cada día y el balance correspondiente.

El lunes sus egresos fueron de 974.25 pesos y el balance fue de 187.32 pesos negativos; el martes tuvo ingresos por 1425.90 pesos y un balance de 574.35 pesos; el miércoles los egresos fueron de 298.40 pesos con un balance de 987.55 pesos; para el jueves tuvo ingresos de 687.24 pesos y un balance negativo de 98.80 pesos y el viernes sus egresos fueron de 187.70 pesos y un balance de 795.85 pesos.

¿Cómo puedes obtener el dato que falta cada día?

En cada caso tienes que hacer una resta, al balance del día tienes que restarle el egreso o el ingreso correspondiente, según sea el caso.

Para el lunes tenemos la resta de dos números negativos, ¿cómo se hace?, observa la imagen:

Aplica el inverso aditivo al sustraendo para convertir la resta, en suma. Nos queda que 187.32 negativo menos 974.25 negativo es igual 187.32 negativo más 974.25.

¿Ahora cómo resuelves esta nueva operación?

Es un caso de la suma de un número negativo con uno positivo.

¿Cómo se resuelve? Hay varias formas de hacerlo.

Una forma es por medio de la diferencia de los valores absolutos.

974.25 menos 187.32 es igual a 786.93.

Por lo tanto, los ingresos del lunes fueron de 786.93 pesos.

Para el día martes tenemos una resta de dos números positivos, 574.35 menos 1,425.90. Y para el miércoles la resta es de un número positivo menos uno negativo: 987.55 menos 298.40 negativo.

Calcula la diferencia entre los valores absolutos y puedes anticipar que el resultado es negativo, porque el sustraendo es mayor que el minuendo.

Para el miércoles, como es una resta de un positivo menos un negativo, puedes aplicar el inverso aditivo del sustraendo y resolvemos una suma.

987.55 menos 298.40 negativo es igual a 987.55 + 298.40 que es igual a 1,285.95

Entonces, los egresos del día martes fueron de 851.55 pesos y los ingresos del miércoles fueron de 1,285.95 pesos, como lo muestra la siguiente imagen:

Observa los resultados que se obtuvieron al hacer los cálculos de jueves y viernes:

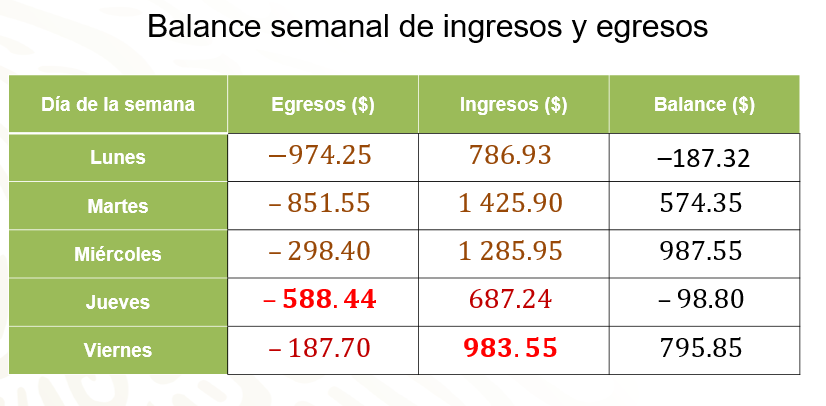
Al resolver la operación 98.80 negativo menos 687.24 el resultado es igual a 588.44 que son los egresos de Eduardo del día jueves. Para calcular los ingresos del viernes, a 795.85 le restas 187.70 negativo, obtienes como resultado 983.55 pesos.

¿Cuál será el balance semanal de Eduardo?, resuélvelo en base a lo que aprendiste en la sesión.

¿Qué pasa si necesitas sumar o restar fracciones positivas y negativas?

En estos casos se siguen los mismos procedimientos vistos con los números enteros y los números decimales, aplicando lo que sabes sobre sumar y restar fracciones positivas.

Observa el siguiente ejemplo:

Se tienen tarjetas con diferentes fracciones positivas y negativas, se tomarán dos al azar y sumarás dichos valores, posteriormente, harás lo mismo, pero para la resta.

Las fracciones son: cinco octavos, un medio, cinco cuartos, dos tercios, cinco medios negativos, cuatro tercios negativos, siete octavos negativos y tres cuartos negativos.

Para resolver cada operación, primero las convertirás a fracciones con igual denominador y después, aplicaremos las reglas vistas para sumar números positivos y negativos.

Después de tomar varias parejas de fracciones para sumarlas, se obtienen tres operaciones de suma, por ejemplo.

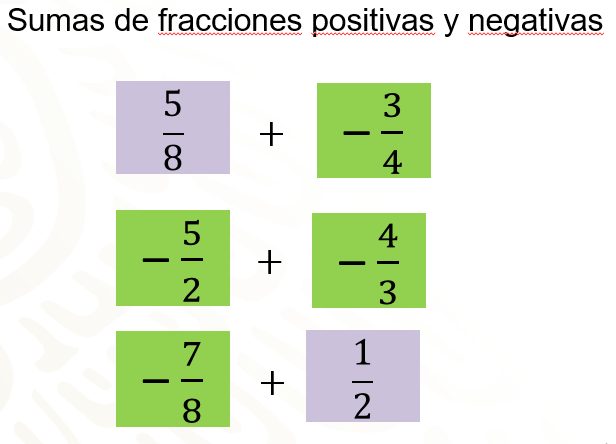
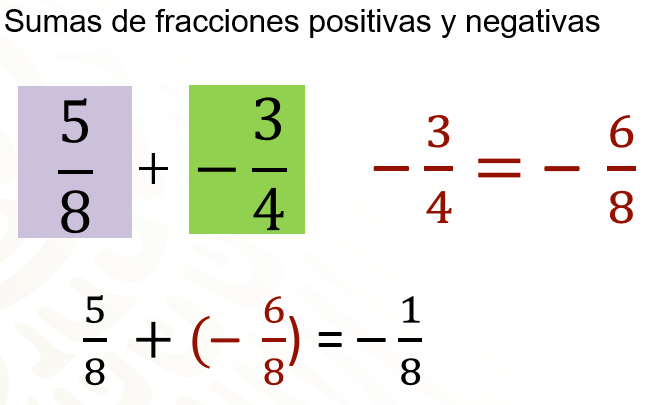
Cinco octavos más 3/4 negativos. Primero convierte 3/4 negativos a 6/8 negativos. Entonces queda que es igual a cinco octavos más 6/8 negativos. Calcula la diferencia de los numeradores: 6 menos 5 igual a 1; y el resultado tendrá el signo del de la fracción cuyo numerador tiene mayor valor absoluto: por lo tanto, cinco octavos más tres cuartos negativos es igual a un octavo negativo.

Para la suma, cinco medios negativos más 4 tercios negativo, convierte a sextos ambas fracciones; quedando la operación 15 sextos negativos más 4 tercios negativos. Suma los valores absolutos de los numeradores y el resultado es negativo porque ambos sumandos son negativos. Por lo tanto: 5 medios negativos más 4 tercios negativos, es igual a 23 sextos negativos.

Para 7 octavos negativos más un medio, convierte un medio a cuatro octavos, obteniendo la suma 7 octavos negativos más 4 octavos, calcula la diferencia de los numeradores, que es 3 y como 7 tiene mayor valor absoluto que 4, el resultado es negativo. Así, 7 octavos negativos más un medio es igual a 3 octavos negativos.

Sin duda que las reglas y procedimientos vistos para operar con números positivos y negativos, como enteros, fracciones o decimales, serán de mucha utilidad

El reto de hoy:

Observa la siguiente imagen y aplica los procedimientos de sustracción.

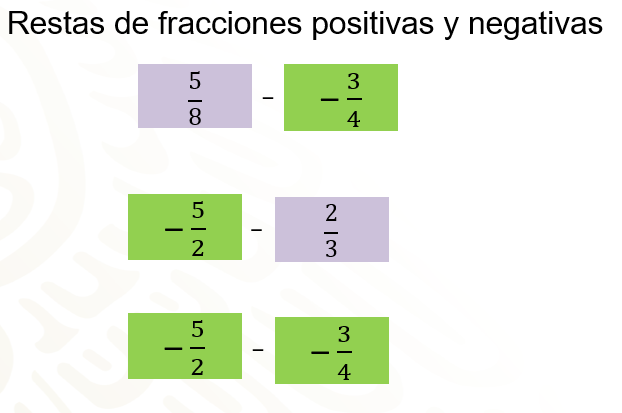
5 octavos menos 3 cuartos negativos, 5 medios negativos menos 2 tercios y 5 medios negativos menos 3 cuartos negativos.

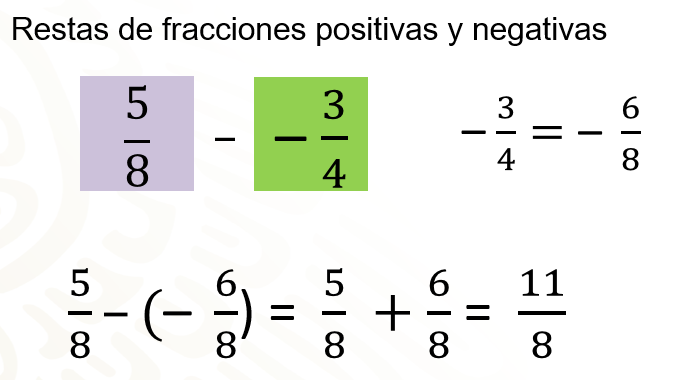
Para 5 octavos menos 3 cuartos negativos, convierte 3 cuartos negativos en 6 octavos negativos y como restar es lo mismo que sumar por el inverso aditivo, entonces, 5 octavos menos 6 octavos negativos es igual a 5 octavos más 6 octavos igual a 11 octavos. Por lo tanto, 5 octavos menos 3 cuartos negativos es igual a 11 octavos.

En el caso de 5 medios negativos menos 2 tercios, convierte ambas fracciones a sextos, y convierte la resta en una suma del minuendo por el inverso aditivo del sustraendo: 15 sextos negativos menos 4 sextos es igual a 15 sextos negativos más 4 sextos negativos que es igual a 19 sextos negativos. Por lo que: 5 medios negativos menos 2 tercios es igual a 19 sextos negativos.

Finalmente, 5 medios negativos, menos 3/4 negativos, es igual a 10 cuartos negativos menos 3 cuartos negativos. Suma 10 cuartos negativos más el inverso aditivo de 3 cuartos negativos. 10 cuartos negativos más 3 cuartos negativos es igual que 10 cuartos negativos más tres cuartos, para resolver la operación calcula la diferencia de los valores absolutos de los numeradores y el resultado será negativo porque 10 es mayor que 3. Por lo tanto, 5 medios negativos menos 3 cuartos negativos es igual a 7 cuartos negativos.

¡Buen trabajo!

Gracias por tu esfuerzo. 

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/