La representación más adecuada
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42
La representación más adecuada
Aprendizaje esperado: convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones usando la notación decimal. Ordena fracciones y números decimales.
Énfasis: identificar la representación más adecuada al ordenar los números decimales y fraccionarios.
¿Qué vamos a aprender?
En esta lección podrás identificar la representación más adecuada al ordenar números decimales y fraccionarios, a partir de situaciones que combinen ambas representaciones numéricas.
Para esta lección necesitarás:
●Cuaderno o papel para tomar notas.
●Lápiz, goma y sacapuntas.
●Libro de texto de Matemáticas para primer grado.
Una pregunta frecuente es, qué representación es más conveniente utilizar, fracciones o sus equivalencias en número decimal. Una de las respuestas más comunes es el uso de una u otra dependiendo del planteamiento, y a veces es mejor utilizar números decimales, pero no siempre. Piensa, ¿qué representación es más conveniente usar: fracciones o números decimales?
¿Qué hacemos?
En ocasiones puede ser útil usar decimales y en otras fracciones, pero, ¿cómo saber cuándo es más conveniente usar uno u otro tipo de representación numérica?
Utilizando diversos ejemplos, se responderá a la pregunta, sin embargo, se considera que exista más de una respuesta. Observa el primer ejemplo.
Ejemplo, granola artesanal
Una empresa familiar se dedica a elaborar distintos tipos de granola de manera artesanal, para ampliar sus ventas, crearon una nueva receta y necesitan considerar las cantidades de ingredientes que involucra para nombrar al producto según el ingrediente predominante. A partir de la receta se deben ordenar los ingredientes de mayor a menor o de menor a mayor, es indistinto, lo importante será identificar al mayor para determinar cuál es el ingrediente principal y así nombrar su nuevo producto.
La receta incluye los siguientes ingredientes para la elaboración de un paquete de granola:
- Una y media tazas de amaranto.
- Una y un tercio de tazas de avena.
- Tres cuartos de taza de pasas.
- 25% (0.25) tazas de almendra troceada.
- Dos tercios de taza de cacahuate troceado.
- 50% (0.5) tazas de coco seco rallado.
Con base en esta situación, para comparar y ordenar las cantidades pueden usarse fracciones o números decimales.
¿Cuál representación consideras que es la más adecuada? ¿Por qué?
Se considera que, tanto los números decimales como las fracciones representan la misma cantidad de cada ingrediente, pero es más común la medición por tazas en las recetas que usan fracciones y por el tipo de números decimales y fracciones que se presentan.
Para el ejemplo, necesitamos ordenar las cantidades de los ingredientes para conocer el predominante y así elegir el nombre del producto. Sin embargo, tanto los números decimales cómo números fraccionarios pueden ser útiles.
La consideración más importante en esta situación es que hay fracciones como 1 1/3 o 2/3 que no tiene una fracción decimal equivalente, por lo tanto, no se pueden representar como un número decimal finito, y éstas son justo algunas de las medidas en fracciones involucradas en la receta, por lo tanto, no puedes expresar todas las medidas en números decimales exactos, es decir, 1 1/3 en notación decimal es 1.33... …infinito y 2/3 es 0.66… infinito, por lo tanto, dos tercios no es equivalente a 1.33… sino que 2/3 es aproximadamente 1.33... …
Con base en esta observación, en este planteamiento es más conveniente utilizar fracciones como la representación más adecuada para comparar las cantidades. Aunque la notación decimal también permite comparar las medidas, porque no quieres obtener cantidades exactas, pero existen casos en los que si se requiere dicha medida, por eso, en casos como este, se opta por la representación como fracción.
Ya has definido la representación más adecuada, ahora corresponde obtener las fracciones equivalentes de los números decimales 0.25 y 0.5, para después ordenar las cantidades de los ingredientes y hallar el ingrediente predominante que corresponde a la fracción mayor.
En primera instancia, hay que establecer la fracción equivalente a 0.25 Como este número se lee: veinticinco centésimos, es posible determinar que la fracción equivalente es veinticinco cienavos que puede simplificarse como cinco veinteavos, misma que puede simplificarse como un cuarto. Para comprobarlo, si se divide 1 entre 4 efectivamente, encontrarás un cociente igual a 0.25, o bien veinticinco centésimos.
Como cero punto cinco es igual a 5 décimos que es igual a un medio. De manera que 0.5 es equivalente también a un medio. Finalmente, corresponde ordenar las fracciones de mayor a menor.
Las cantidades expresadas como números mixtos o fracciones quedan de la siguiente manera:
- Una y media tazas de amaranto.
- Una y un tercio de taza de avena.
- Tres cuartos de taza de pasas.
- Un cuarto de taza de almendra troceada.
- Dos tercios de taza de cacahuate troceado.
- Media taza de coco seco rallado.
Para comparar y ordenar las medidas, se recurre a la recta numérica. En este caso usa 3 rectas numéricas, con la misma escala del 0 al 2, una seccionada en tercios, otra en cuartos y otra en medios. Así es posible ubicar todas las medidas involucradas, como se muestran a continuación.
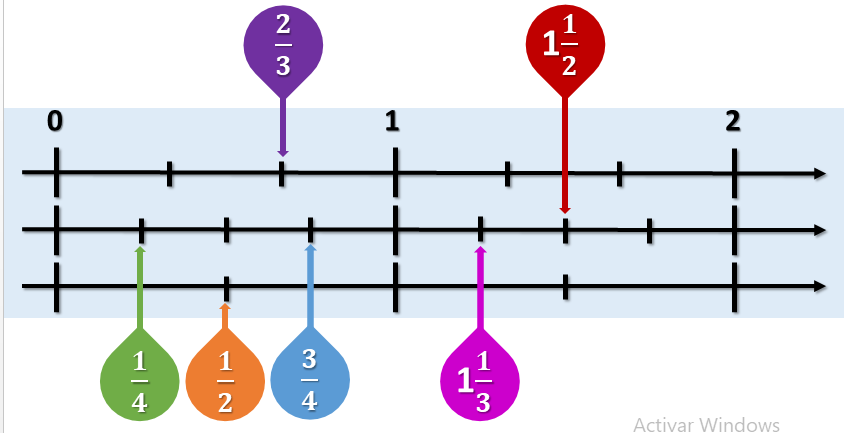
- Un entero y un medio
- Un entero y un tercio
- Tres cuartos
- Un cuarto
- Dos tercios
- Un medio
Para determinar cuál es la fracción mayor, puedes ordenarlas de mayor a menor o de menor a mayor, es indistinto. En este caso lo harás de menor a mayor:
- Un cuarto
- Un medio
- Dos tercios
- Tres cuartos
- Un entero y un tercio
- Un entero y un medio

Cómo puedes observar, el número mayor es uno y medio y el menor es un cuarto. Amaranto es el ingrediente que predomina en la receta.
A continuación, analiza el siguiente ejemplo para que te sea más fácil poder identificar más elementos que permitan determinar qué representación es la más adecuada al comparar fracciones y decimales.
Revisa el siguiente ejemplo.
Ejemplo, fertilizantes
En un laboratorio de Biología se realizan pruebas para la creación de fertilizantes orgánicos en beneficio de cultivos alimentarios. Para este ejemplo, se considera que se rociaron 5 plantas con distintos fertilizantes, para determinar su posible efecto en el crecimiento de las plantas, ya que se cultivaron en las mismas condiciones y la diferencia radica en el fertilizante utilizado en cada una durante su cultivo.
Después de aplicar de manera constante el fertilizante durante 30 días a las cinco plantas, dos laboratoristas se encargaron de medir su altura.
Los laboratoristas reportaron las siguientes alturas:
El laboratorista 1, reportó que la altura de la planta 1 fue de tres cuartos de metro mientras que la altura de la planta 2 fue de dieciocho veinticincoavos de metro. Por otro lado, el laboratorista 2, reportó que la altura de la planta 3 fue de 0.73 metros, la altura de la planta 4 fue de 0.77 metros y que la altura de la planta 5 fue de 0.69 metros.
Para organizar el informe global y poder comparar el crecimiento de las plantas, se tienen que ordenar las medidas de mayor a menor altura. Piensa ¿cuál de las plantas alcanzó mayor altura?, ¿cuál menos?, ¿cuál representación sería la más adecuada para comparar las alturas?
Recuerda que es importante considerar los beneficios de ambas representaciones, para determinar cuál es la más adecuada para comparar y ordenar las alturas obtenidas, ya sea que se elija representar los resultados como fracciones o como números decimales, se tendrán que obtener equivalencias, ya que se encuentran representaciones combinadas.
Es importante saber que cuando las fracciones no tienen un denominador común, podrían requerirse más cálculos para ordenarlas, primero se tendría que buscar un común denominador en todas las fracciones y después, convertirlas a su equivalente con dicho denominador. Además, en este caso, al comparar números decimales que se encuentran en un rango cercano, existe mayor facilidad para ordenar de mayor a menor. Aunque un criterio que se podría considerar es verificar si las fracciones involucradas tiene una fracción decimal equivalente. Si fuera el caso, comparar fracciones decimales podría ser una buena opción también.
Estos criterios sin duda te resultarán muy útiles para decidir que tipo de números usar
Reflexiona: ¿Cuál es el proceso que seguirás para ordenar las medidas como números decimales? Compara tu respuesta con los pasos que seguirás a continuación.
Antes de ordenar las medidas, realiza las equivalencias. Primero usa la representación decimal, debido a:- La cercanía del rango en el que se encuentran los números.
- Que hay menos operaciones que realizar, es decir, el proceso es más corto, ya que hay menos fracciones que número decimales.
Entonces, primero debes obtener las equivalencias de las alturas de las plantas 1 y 2 que corresponden a las fracciones tres cuartos y dieciocho veinticincoavos, respectivamente, número decimal. Para ello, se divide el numerador entre el denominador para cada fracción. La equivalencia decimal de la fracción tres cuartos: 3 entre 4 es igual a 0.75. Enseguida, procedes a encontrar la equivalencia decimal de la fracción dieciocho veinticincoavos: 18 entre 25 es igual a 0.72.
Ahora sí, puedes ordenar las alturas de las plantas que se encuentran representadas en números decimales.
La forma de hacerlo es comparar cifra con cifra cada uno de los números. En este caso, primero compara la posición de los décimos y luego la de los centésimos, por lo que encuentras el siguiente orden de mayor a menor, en las alturas de las plantas:
Primero, la planta 4 con 0.77metros de altura, luego la planta 1 con 0.75 metros de altura, enseguida la planta 3 con 0.73metros de altura, luego la planta 2 con 0.72metros de altura y finalmente, la planta 5 con 0.69metros de altura.

Usar como representación a los números decimales para las alturas de las plantas es una buena opción. Ahora observa el mismo procedimiento, pero usando fracciones.
Lo primero que debes hacer es obtener las fracciones decimales equivalente a 3/4 y 18/25. Al dividir 10 entre 4, el resultado no es exacto, ya que 10 entre 4 es igual a 2.5 y como 10 es menor al denominador 25, por ello, se divide entre 100.
Divide 100 entre 4, cuyo resultado es igual a 25. Después, se multiplica a 3 y a 4 por 25 para obtener la fracción decimal equivalente.
Ahora, divide 100 entre 25 que es igual a 4, y el numerador y el denominador de 18/25 los multiplicas por 4, al resolver las operaciones, la fracción decimal equivalente es 72/100.

Ahora únicamente tienes que convertir los números decimales a fracción decimal, es decir, que para la planta 3 que mide 0.73 m, su medida equivalente como fracción decimal es 73 sobre 100, 73 centésimos, la planta 4, 77 centésimos y la planta 5, 69 centésimos.
Ya que tienes las medidas como fracciones decimales, las ordenas, como a continuación se muestra

Se corrobora que la planta con mayor altura es la 4, con 77 centésimos de metro y la de menor altura es la 5, con 69 centésimos de metro.
En los ejemplos anteriores observaste que para ordenar cantidades que involucran fracciones y decimales, es posible trabajar con la fracción o su expansión decimal, según sea el caso, ahora qué sucede si tienes que operar con dichas cantidades, es decir, que las utilizarás para realizar un cálculo.
Observa la siguiente capsula del segundo. 0:45 al 01:30.
- Una vuelta y media
Como pudiste observar, en esa situación se debe multiplicar la medida de la pista, es decir 360 metros por cada una de las fracciones registradas en cada recorrido diario, puede ser una forma más eficiente de operar con números decimales.
Ahora analiza el siguiente caso:
El lunes corrió 1 1/4 el martes 1 1/2, el jueves 2 3/8, el viernes 3 3/5 y el sábado 5 1/5.
- El número mixto 1 1⁄4 es equivalente al número decimal 1.25.
- El número mixto 1 1/2 es equivalente a 1.5.
- El número mixto 2 3/8 es equivalente a 2.375.
- El número mixto 3 3/5 es igual al número decimal 3.6.
- Y el número mixto 5 1/5 es equivalente a 5.6.
En este caso todos los números mixtos, pudieron representarse como un decimal finito ya que su expansión decimal fue exacta y se tiene la libertad de decidir si se trabaja con fracciones o con decimales ya que en cualquiera de los casos se llegará al mismo resultado. Piensa ¿con qué tipo de números prefieres operar?
El reto de hoy:
Calcula la distancia recorrida para cada día de la semana
Los días que corrió fueron: lunes, martes, jueves viernes y sábado. En la siguiente columna multiplica el número de vueltas por la medida de la pista que es de 360 metros, así: 1.25 por 360, 1.5 por 360, 2.375 por 360, 3.6 por 360 y 5.6 por 360.

En la última columna se observan las respuestas que representan los recorridos en metros: el lunes fueron 450 metros; el martes, 540 metros; el jueves, 855 metros; viernes, 1 296 metros y sábado, 2 016 metros
En conclusión; existe una representación adecuada dependiendo de la situación y que a partir de tus conocimientos y pericia matemática puedes encontrarla. Así decidirás si usas a los números decimales o los fraccionarios.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion