Orden de las fracciones y decimales

Orden de las fracciones y decimales

Aprendizaje esperado: convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones usando la notación decimal. Ordena fracciones y números decimales

Énfasis: resolver problemas de orden de las fracciones y decimales, usando unidades de medida.

¿Qué vamos a aprender?

En esta lección estudiarás las relaciones de orden entre los números decimales y fraccionarios en contexto de medidas.

Para empezar, compararás y ordenarás diferentes listones, usando como unidad de referencia el tamaño de un listón de 1m de longitud. Si es posible, consigue listones, varitas u otros materiales similares para realizar la actividad.

¿Qué hacemos?

Observa la siguiente imagen.

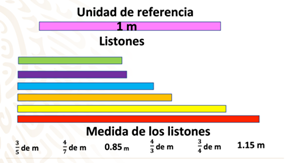
La imagen representa un listón rosa que mide 1 metro de largo y seis listones de diferentes colores y tamaño y la medida que les corresponde como fracción o número decimal. Las medidas son, tres quintos de metro, cuatro séptimos de metro, 0.85 metros, cuatro tercios de metro, tres cuartos de metro y 1.15 metros.

Reflexiona en torno a las siguientes preguntas:

¿Cómo podrías determinar qué medida le corresponde a cada listón? ¿Qué fracción o número decimal le corresponde al listón más pequeño? ¿Cuál al listón más grande?

Lo primero que tienes que hacer es obtener las medidas en la misma representación numérica, ya sea como número decimal o como fracción para poder compararlas.

Pero otra cuestión que también tienes que considerar es que dos listones, el amarillo y el rojo son más largos que el rosa.

Analiza las medidas, en la siguiente imagen:

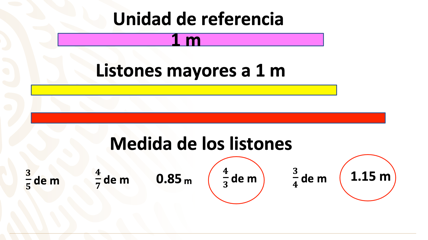
Primero aquellas que están dadas con números fraccionarios. En estos casos, tienes tres fracciones propias, es decir, fracciones en las cuales el numerador es menor que el denominador: 3/5, 4/7 y 3/4, por lo tanto, representan medidas menores a un metro.

La fracción 4/3 es impropia, lo que significa que es mayor que uno. En el caso de los números decimales, 0.85 es menor que uno y 1.15 es mayor que uno, por lo tanto, ya tienes las medidas de los listones amarillo y rojo.

Ahora piensa:

Podrías convertir 4/3 a número decimal, pero esta fracción no tiene un número decimal equivalente, ya que le corresponde un número decimal infinito. Entonces, sería mejor que conviertas 1.15 a fracción para hacer la comparación, pero como en este caso no vas a conocer la medida exacta, solamente vas a hacer una comparación, entonces puedes usar números decimales, es decir, una aproximación a 4/3, al dividir 4 entre 3 es resultado es aproximadamente igual a 1.33, y si lo comparas con 1.15, vemos que 4/3 es mayor.

Ahora ya sabes que el listón amarillo mide 1.15 m de largo y que el listón rojo, que es el más grande en longitud, mide 4/3 de m.

Ahora determina cuál es la medida del listón más pequeño, ordenando las medidas menores a un metro.

Conoces que las medidas son: 3/5 de m, 4/7 de m, 0.85 metros y 3/4 de metro.

Analiza las siguientes preguntas en torno a las medidas que acabas de observar:

¿Ya sabes cuál es la medida del listón verde que es el más pequeño en longitud? ¿Qué tipo de representación resulta más conveniente para comparar las medidas?

En este caso, podrías utilizar fracciones para realizar la comparación, porque 4/7 no tiene una representación exacta como número decimal, pero el proceso sería más largo, ya que tienes que buscar un común denominador y después realizar la conversión a fracciones equivalentes con igual denominador, y como únicamente vamos a comparar, podemos convertir las fracciones a número decimal.

Así tienes que, 3 entre 5 es igual a 0.6, 4 entre 7 es aproximadamente 0.571 y 3/4 es igual a 0.75.

Ahora ya puedes comparar las medidas, el listón verde que es el de menor tamaño mide 4/7 de m, el morado, 3/5 de m, el azul 3/4 de m y el anaranjado 0.85 m.

Observa la siguiente imagen:

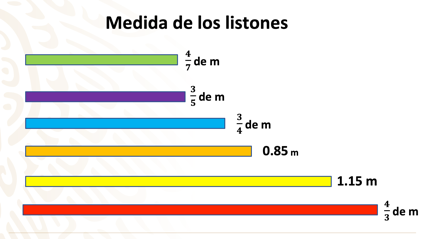
Así tienes que las medidas de los listones, ordenadas de menor a mayor en metros son: 4/7, 3/5, 3/4, 0.85, 1.15 y 4/3.

Con los ejemplos anteriores, pudiste establecer una estrategia que permite comparar números decimales y fracciones, pero sin duda, existen muchas otras situaciones en las que te puedes enfrentar a la necesidad de comparar este tipo de números.

Analiza el siguiente planteamiento:

Ejemplo, elaboración de joyas

“Hugo y Antonio son socios y se dedican a elaborar joyas de diferentes metales, entre ellas, alhajas de oro. Como el oro es considerado un metal blando, tienen que aliarlo con otros elementos para que obtenga dureza. Una aleación es una mezcla homogénea de dos o más elementos, de los cuales al menos uno debe ser un metal.

Hugo hizo una sortija y un collar de oro, y Antonio unos aretes y una pulsera. Al calcular la proporción de oro que utilizaron en cada pieza, cada uno registró la información de diferente forma”:

Observa la siguiente imagen que contiene una tabla de las joyas que hizo cada uno y la cantidad de oro en su composición.

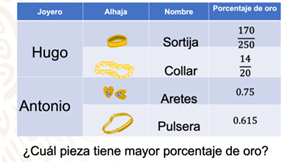
La primera fila muestra la sortija que hizo Hugo cuya composición de oro es de 170/250 de oro, la segunda fila corresponde al collar de Hugo, con 14/20 de oro, posteriormente se muestran las piezas que hizo Antonio; los aretes con 0.75 y la pulsera de 0.615.

¿Cuál pieza tiene mayor porcentaje de oro?

¿Cómo podrías ordenar y comparar las fracciones y números decimales para saber que pieza tiene mayor porcentaje de oro?

Primero identifica si las fracciones 170/250 y 14/20 tienen una fracción decimal equivalente, que en este caso es con denominador mil.

¿Cómo puedes obtener una fracción equivalente con denominador mil?

Lo primero es determinar si los denominadores son múltiplos entre sí, es decir, si uno cabe de manera exacta en el otro, de lo contrario no podríamos convertir esa fracción.

En el caso de la sortija, la proporción es de 170/250, y quieres convertir la fracción a milésimos.

Primero verifica si hay un número entero que multiplique a 250 y dé como resultado 1000.

Para ello divide 1000 entre 250, resuelve la división y obtienes como cociente 4, por lo que multiplicarás el numerador y el denominador de la fracción por 4 para obtener la fracción equivalente.

Así tenemos 170/250 es equivalente a 680/1000.

Se sabe que este procedimiento también es útil para establecer la fracción equivalente a 14/20.

Pero ¿qué sucede con los números decimales?

En el caso de los números decimales 0.75 y 0.625, sabes que 0.75 o leído de forma correcta 75 centésimos, es equivalente a 75/100.

Y en el caso de la pulsera 0.615 es equivalente a 615 milésimos, es decir 615/1000 Y en este caso ya tenemos la fracción en milésimos.

Ahora, convierte a milésimos las medidas del collar y los aretes.

Para el collar divide mil entre 20 dando como resultado 50, número por el cual multiplicamos el numerador y el denominador de 14/20, obteniendo la fracción 700/1000.

Ahora en los aretes 100 es la décima parte de mil, por lo que multiplicamos el numerador y el denominador de la fracción 75/100 por 10, para obtener la fracción equivalente que es 750/1000.

Por último, la pulsera, expresada como fracción decimal es equivalente a 615/1000.

Observa la siguiente imagen que muestra el procedimiento:

Con estos datos, ya puedes comparar las cantidades, porque todas están dadas en milésimos. Regresemos a la tabla de datos.

Observa la siguiente imagen que muestra el porcentaje de oro de las piezas ordenadas de menor a mayor.

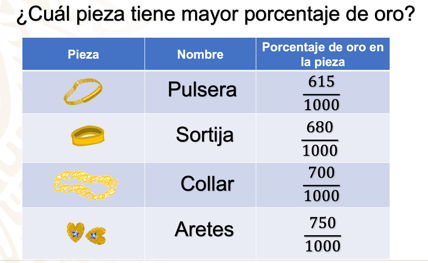
Así puedes ver que la pieza con menos porcentaje de oro es la pulsera con 615/1000, la segunda es la sortija con 680/1000, la tercera pieza es el collar con 700/1000 y finalmente, la pieza con mayor porcentaje de oro son los aretes con 750/1000 de oro.

Al convertir fracciones y números decimales a fracciones decimales, podemos compararlas y ordenarlas.

Ahora que comprendiste, a ordenar fracciones y decimales, observa la siguiente imagen que contiene una lista de alimentos con la cantidad de hierro que pueden llegar a contener, por cada 100 gramos. Es importante que anotes los valores aquí presentados.

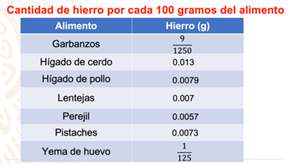
¿Cuál de estos alimentos contiene una mayor cantidad de hierro?

Observa que la tabla contiene fracciones y números decimales, pero a diferencia de la situación anterior, te conviene convertir las fracciones a número decimal, porque únicamente son dos cantidades dadas como fracción

Recuerda que para convertir una fracción en número decimal divides el numerador entre el denominador, tal como lo muestra la siguiente imagen:

Ahora ordena de menor a mayor los alimentos por su contenido en Hierro. Al tener todas las cantidades en decimales las alineas con el punto decimal y, para facilitar la comparación, agregas ceros a la derecha, de manera que todas tengan el mismo número de cifras.

Igualar el número de cifras es muy útil al ordenar número decimales, recuerda que el número entre más cercano al punto decimal es mayor.

La siguiente tabla muestra las cantidades en gramos:

En este momento ya es más fácil compararlos y ordenarlo.

Observa la siguiente tabla

Gracias a esta comparación y ordenamiento puedes saber que uno de los alimentos que contiene mayor cantidad de hierro por cada 100 gramos es el hígado de cerdo. Aunque no hay nada mejor que tener una dieta bien balanceada ya que hay otros alimentos como el arroz o germen de trigo que también contienen hierro en diferentes proporciones.

El reto de hoy:

Aplica lo aprendido en el siguiente desafío.

Se tiene un clavo. Se sabe que su medida es de la mitad de una pulgada. ¿Cuál de las siguientes medidas es la mejor aproximación de su longitud?

1. 1.2 cm
2. 1 cm y tres catorceavos de centímetro
3. 1.3 cm

Dado que cuentas con la información del valor de una pulgada en centímetros, es necesario comparar las medidas en el mismo tipo de representación numérica.

En este caso, conviene que sea en números decimales

El razonamiento para seguir es saber la medida de la longitud del clavo en centímetros, para ello consideremos que:

Si una pulgada es igual a 2.54 cm

Media pulgada es igual a 1.27 cm.

Es decir, se puede dividir 2.54 entre 2 o multiplicar 2.54 por un medio. Ahora, ya sabemos que la longitud del clavo es de 1.27 cm de largo.

¿Cuál de las siguientes medidas es la mejor aproximación de la longitud del clavo?,

Necesitas comparar 1.27 con cada una de las medidas de las opciones.

Analiza lo siguiente:

Al comparar 1.2 cm y 1.27 cm identificamos que 1.27 es mayor que 1.2 por 0.07 centésimas de centímetro o que 1.2 es menor que 1.27.

Al comparar 1 cm y tres catorceavos de centímetro, necesitamos conocer el equivalente de tres catorceavos de centímetro en número decimal.

Para ello dividimos 3 entre 14 y sabemos que es aproximadamente 0.21 cm, es decir, 1.21 cm.

Por lo tanto, y para fines de la comparación, se puede decir que:

1 cm y tres catorceavos de centímetro es menor que 1.27. La diferencia entre ellos es de 0.06 décimas de centímetro.

Al comparar 1.3 y 1.27 identificamos que 1.3 es mayor que 1.27 cm, esto por 0.03 décimas de centímetro.

Hasta aquí has determinado todas las medidas en su expresión como número decimal y las has comparado una por una, pero la pregunta planteada te lleva a un razonamiento más fino:

¿Cuál de las siguientes medidas es la mejor aproximación de la longitud del clavo?

Es decir, tienes que determinar qué medida en número decimal es más cercana a 1.27 que es la medida del clavo.

Has determinado que:

• 1.2 es menor por 0.07 con respecto a 1.27 cm
• 1.21 es menor por 0.06 con respecto a 1.27 cm
• 1.3 es mayor a 1.27 por 0.03 cm, por lo tanto, emplearemos la recta numérica como recurso para argumentar cuál es la mejor aproximación de la longitud del clavo.

Observa la siguiente imagen:

Ubica en la recta numérica el punto que representa la medida de la longitud del clavo que es media pulgada. Después se ubica el punto A que representa la medida de 1.2 cm; asimismo se ubica el punto B que representa la medida de 1 cm tres catorceavos de centímetro en número decimal y el punto C representa la medida de 1.3 cm.

Al observar la ubicación en la recta de los puntos A, B y C, se concluye que la mejor aproximación de la longitud del clavo es 1.3 cm.

¡Buen trabajo!

Gracias por tu esfuerzo. 

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/