Fracciones decimales
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:37Fracciones decimales
Aprendizaje esperado: notación desarrollada de números naturales y decimales. Valor posicional de las cifras de un número.
Énfasis: determinar fracciones decimales y establecer comparaciones entre ellas a partir de la división sucesiva en 10 partes de una unidad.
¿Qué vamos a aprender?
Reforzarás lo aprendido en el tema de las fracciones decimales y establecerás comparaciones entre ellas.
¿Qué hacemos?
Para comenzar debes recordar que los números decimales representan partes menores que un entero, cada una de estas partes las puedes expresar o representar como una fracción o como un número a los que puedes llamar decimal y que para su escritura emplea el punto decimal.
Para estos ejercicios vas a utilizar cuadrados-unidad, los cuales ya conoces.

En este primer trimestre has conocido las siguientes representaciones.
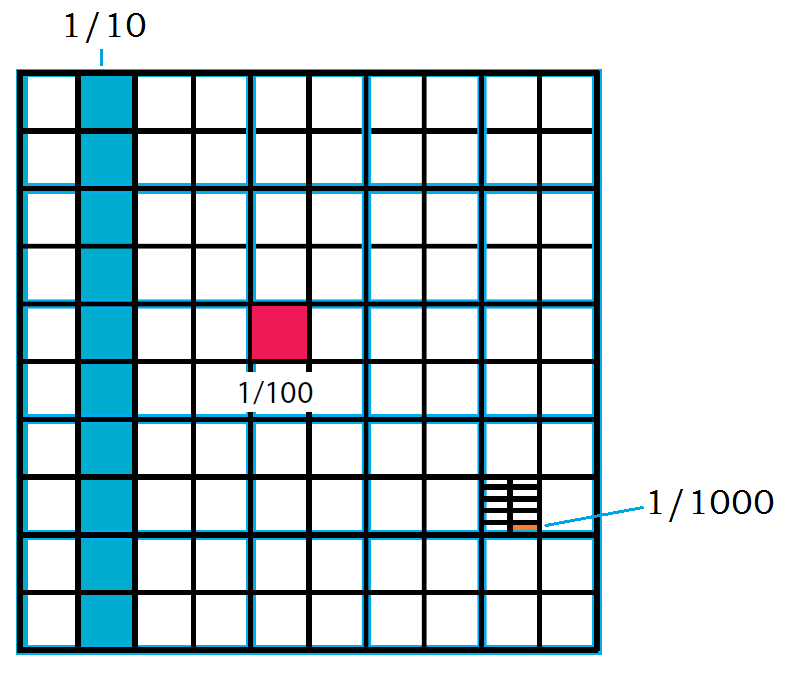
1/10 que representan una de 10 partes y se le como un décimo, 1/100 que representa una de cien partes y se lee como un centésimo y 1/1000 que representa una de mil partes y se lee como un milésimo.
La notación decimal escrita en fracciones, o con el puto decimal queda de la siguiente manera:
Un decímetro: 1 /10 = 0.1
Un centímetro: 1/ 100 = 0.01
Un milímetro: 1/ 1000 = 0.001
Vas a dar respuesta a algunos cuestionamientos iniciales.
- ¿Cuántos décimos caben en una unidad?
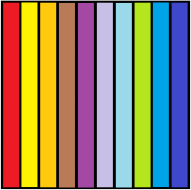
Como puedes apreciar en la imagen en una unidad hay 10 décimos. - ¿Cuántos centésimos caben en un décimo?

Como puedes apreciar en la imagen en un décimo hay 10 centésimos. - ¿Cuántos milésimos caben en un centésimo?

Como puedes apreciar en la imagen en un centésimo hay 10 milésimos.
Así puedes afirmar que:
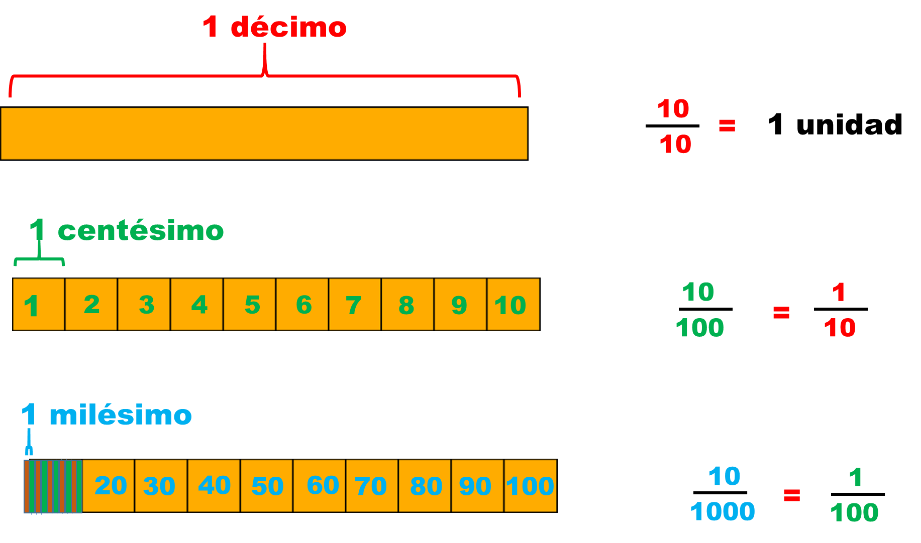
Vas ahora a representar con el apoyo de los cuadros-unidad las siguientes cantidades: 1 décimo = 1/10 = .1
1 décimo = 1/10 = .1
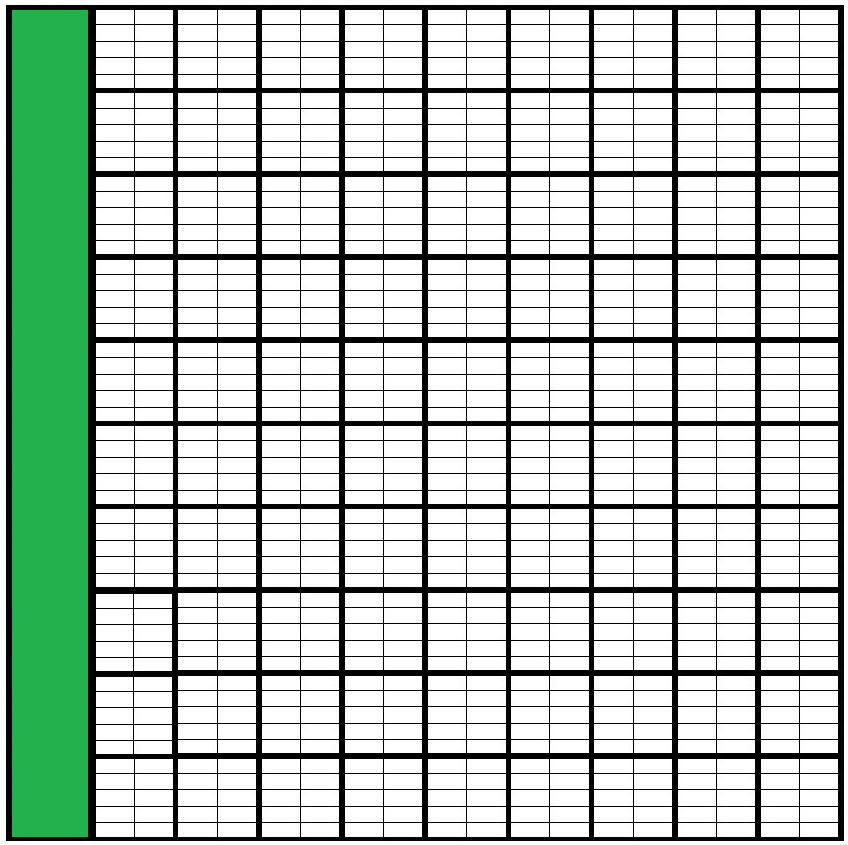
Ahora representaremos: 8 décimos = 8/10 = .8
8 décimos = 8/10 = .8
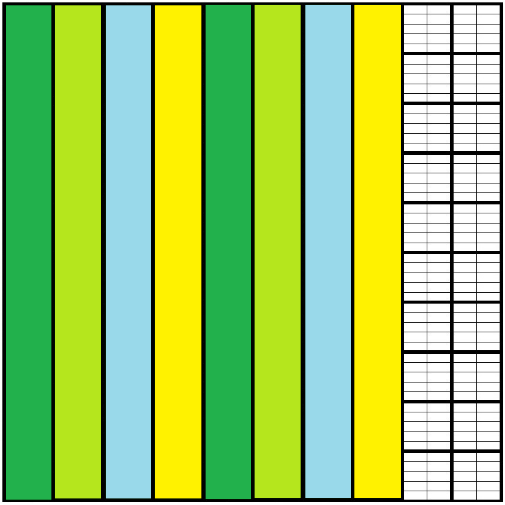
Observa como representarías: 12 centésimos = 12/100 = .12
12 centésimos = 12/100 = .12

Representa: 14 milésimos = 14/1000 = .014
14 milésimos = 14/1000 = .14
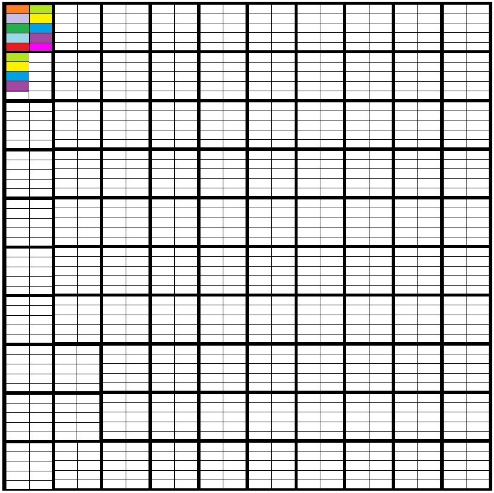
Observa una última representación: 1 entero 8 centésimos = 1 8/100 = 1.08
Vas a leer y escribir algunas cantidades que representan la misma parte del entero, mediante escrituras equivalentes, observa un ejemplo:
Como puedes concluir al observar las imágenes tanto las fracciones decimales como sus escrituras con punto decimal, representan la misma parte del entero.
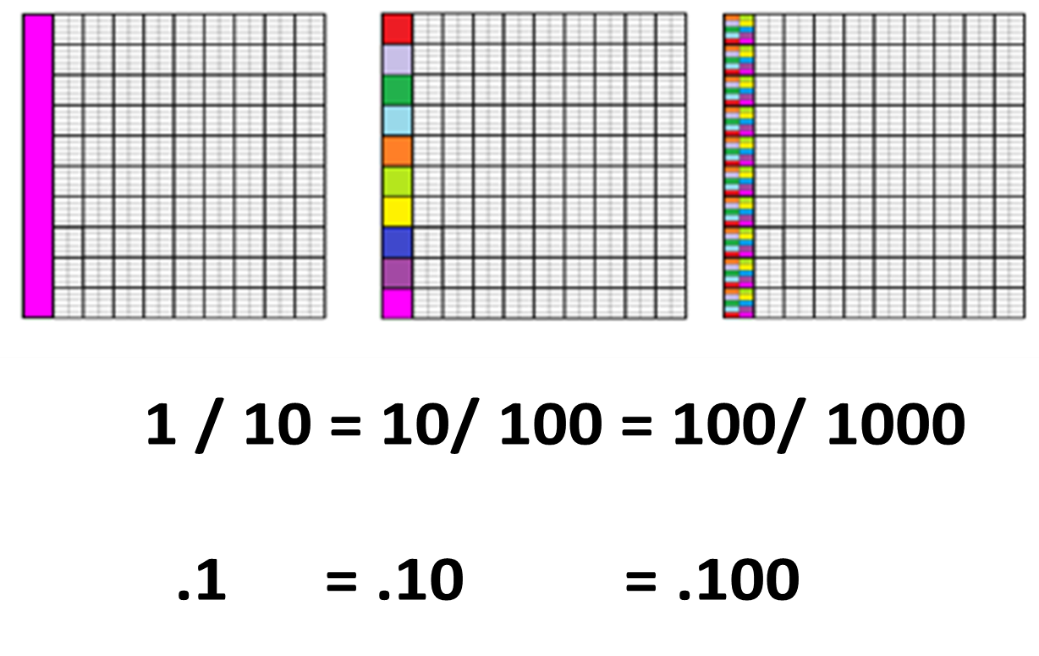
Recuerda ¿Qué son las fracciones decimales?
Las fracciones decimales son aquellas en donde el denominador es una potencia de 10, es decir, es el resultado de multiplicar el 10 por sí mismo un número determinado de veces, por ejemplo:
10x1= 10 (multiplicado una vez).
10X10=100 (multiplicado dos veces) 10x10x10= 1000 (multiplicado tres veces).
| Las fracciones decimales son aquellas en donde el denominador es una potencia de 10, es decir, es el resultado de multiplicar el 10 por sí mismo un número determinado de veces, por ejemplo: 10 X 1 = 10 (multiplicando una vez). 10 X 10 = 100 (multiplicado dos veces). 10 X 10 X 10 = 1000 (multiplicado tres veces). |
Observa un ejemplo:
Las fracciones decimales tienen la particularidad de que pueden representarse de otra manera: utilizando escrituras que llevan punto decimal dando lugar a los números decimales, las cuales sirven para expresar al igual que las fracciones decimales una cantidad menor que la unidad.
Recuerda que los números decimales utilizan el punto para indicar a quien lo lee, que la cantidad escrita es menor que la unidad, por ejemplo:
.2 (esta cantidad representa dos décimas parte del entero) .06 (esta cantidad representa 6 centésimas, nos indica que solo están considerados 6 partes de 100) o .020 (que nos informa que una unidad se dividió en mil partes de las cuales sólo tomamos en cuenta 20).
Una manera de comprobar la escultura decimal, es utilizando los cuadros de unidad, observa la siguiente imagen:
Como puedes apreciar en las imágenes dos décimos es mayor que seis centésimos y seis centésimos es mayor que veinte milésimos.
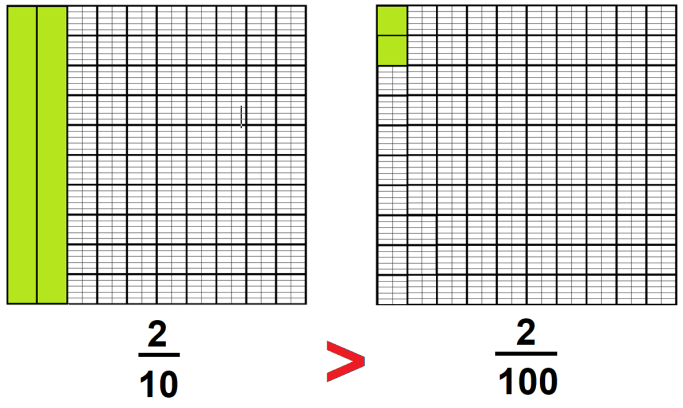
Vamos a comparar algunas fracciones decimales, ¿Qué es más grande 1/10 (léase dos décimos) o 2/100 (léase dos centésimos).
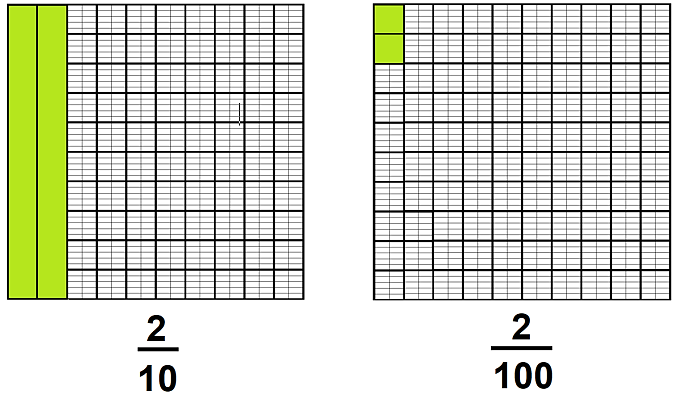
Observa que dos décimos es mayor que dos centésimos, lo cual se indica con el símbolo “mayor que” que con rojo se destaca en la imagen.
Veamos otro ejemplo. ¿Qué es más grande 8/1000 (léase ocho milésimos) o 6/100 (léase seis centésimos).
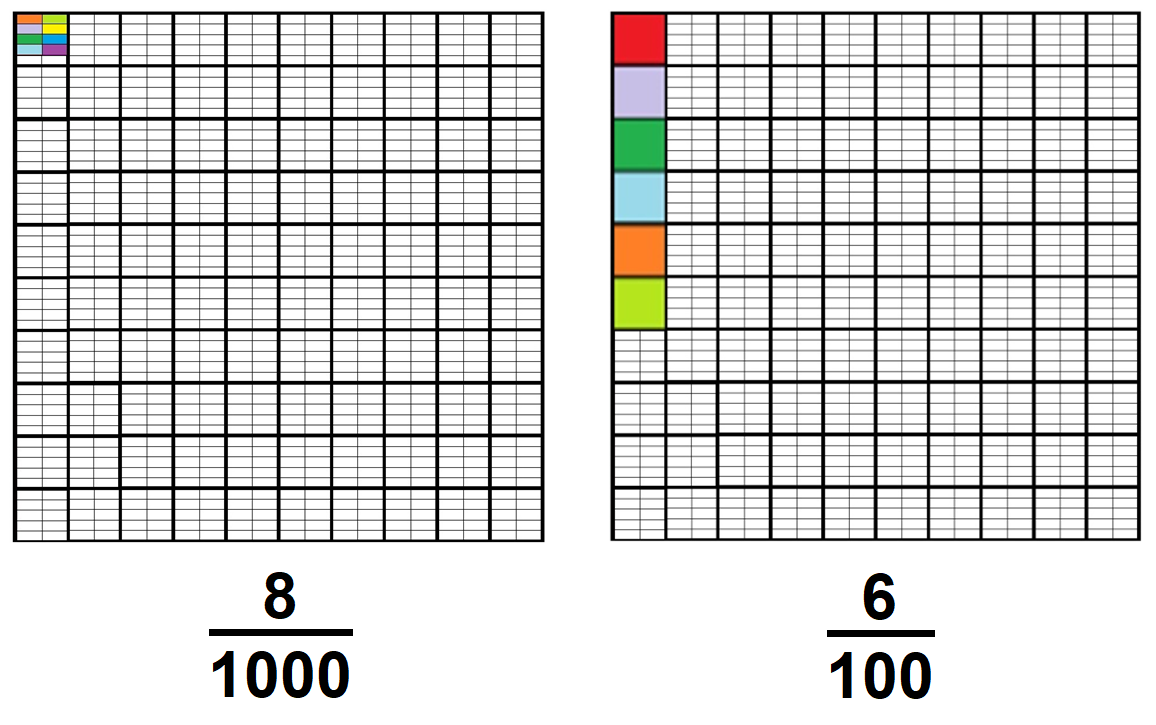
Observamos que ocho milésimos es menor que seis centésimos, lo cual indicamos con el símbolo “menor que” que con rojo se destaca en la imagen.

Para finalizar recuerda que:
| Existen diversas formas matemáticas para representar una misma cantidad, una de ellas es el sistema de numeración decimal que es posicional, donde las cifras de un número tienen un valor que depende de la posición que ocupan, a excepción del cero ya que donde lo escribimos nos indica una ausencia de valor. Por ejemplo: 2890 (2 unidades de millar = 2x1000=2000) (8 centenas = 8 x 100 = 800) (9 decenas = 9 x 10 = 90) (0 unidades = 0x1=0) |
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas









Login to join the discussion