Ecuaciones ¿Debo o tengo? Ese es el dilema

Aprendizaje esperado: Resuelve problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos.

Énfasis: Operar con números enteros. Regla de los signos.

¿Qué vamos a aprender?

Resolverás problemas mediante la formulación y solución algebraica de ecuaciones lineales.

¿Qué hacemos?

Las ecuaciones están presentes en el día a día; sin embargo, cuando escuchas el tema o lees “la representación ax + b = c”, te pueden parecer ajenas o que sólo se refieren a temas que, al parecer, no tienen una aplicación en la vida diaria. Pero ¿recuerdas el concepto de ecuación?

Ten siempre presente que una ecuación es una igualdad que contiene una o más incógnitas. Puedes modelar una o varias ecuaciones asociadas a una situación con la finalidad de encontrar un valor desconocido.

Antes de comenzar a plantear las ecuaciones, recuerda las partes y elementos que componen una ecuación.

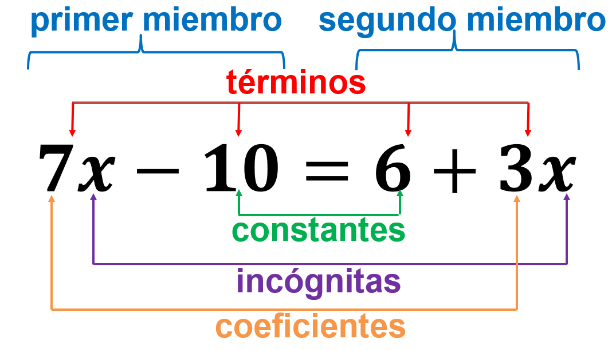
Como observas, la ecuación 7x-10=6+3x está compuesta de dos miembros: el primer miembro está a la izquierda del signo igual de la ecuación, y el segundo, a la derecha. Las incógnitas o valores desconocidos se representan con la literal “x”, y los coeficientes, en este caso, son el número 7 y el número 3, mientras que las constantes son 10 negativo y seis positivo.

A continuación, aplicarás ecuaciones usando de ejemplo una situación cotidiana.

Un chofer que maneja un taxi en la Ciudad de México todas las mañanas, hace diferentes viajes; cabe mencionar que en la Ciudad de México los taxis cobran una cuota llamada “banderazo”, que es una cuota inicial por el uso del servicio, y es de $8.74. Y por cada minuto transcurrido cobra $1.43. Esta cuota puede cambiar según el horario y el lugar donde se tome el taxi, pero, para esta situación, usarás esos datos. Si el chofer cobró en un viaje $47.35, y consideras que esta vez el cobro se realizó por los minutos del viaje, ¿cuánto tiempo duró el viaje?, ¿qué ecuación representa la situación anterior?

Una forma de resolver la situación es modelar o plantear una ecuación donde sólo se van a sustituir los valores.

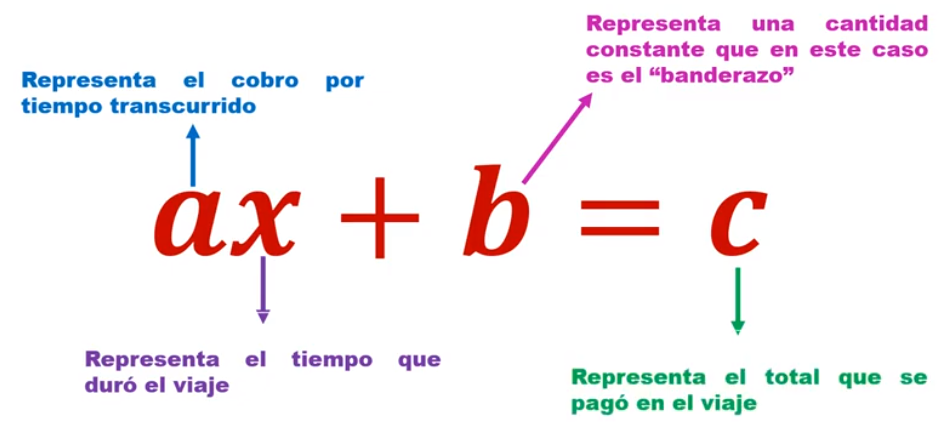
Los datos del problema son los siguientes:

• El banderazo, que es igual a $8.74
• Por cada minuto transcurrido se paga $1.43
• El cobro total del viaje que fue de $47.35.

Las preguntas son: ¿cuánto tiempo duró el viaje?, ¿qué ecuación representa la situación anterior?

La ecuación que representa la situación es:

1.43x+8.74=47.35

Aplicarás la propiedad uniforme y restarás 8.74 en ambos miembros de la ecuación.

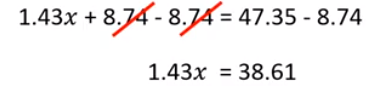
Para despejar a “x” vuelve a aplicar la propiedad uniforme y dividirás a ambos miembros entre 1.43.

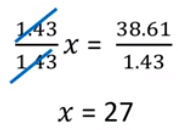
Comprueba sustituyendo el valor de x en la ecuación original.

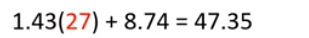
Simplifica el primer miembro.

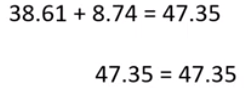
Por lo tanto, el valor de “x” es correcto, porque corrobora la igualdad de la ecuación.

Así se puede concluir que el viaje duró 27 minutos, y la ecuación que representa la situación es: 1.43x+8.74=47.35.

Las propiedades de igualdad te ayudarán a resolver ecuaciones y a establecer una comparación de valores representada por el signo igual, que es el que separa el primer miembro del segundo miembro. Para profundizar más en el tema, observa el siguiente video, en el que podrás conocer las propiedades de la igualdad que utilizarás para la solución de ecuaciones.

1. 1.Propiedades de la igualdad.

https://youtu.be/m1NaOMa_1Yw

Existen más formas en que puedes modelar una ecuación y también requieren de la aplicación de las propiedades de la igualdad.

Ahora analizarás una situación donde aplicarás una ecuación del tipo ax+b=cx+d. Dicha forma de ecuación la trabajarás a partir de la siguiente situación:

El perímetro de un triángulo equilátero está representado por la expresión 7.5x+24, y tiene la misma longitud que el perímetro de un trapecio isósceles, cuyo perímetro está representado por la expresión 4x+44.3.

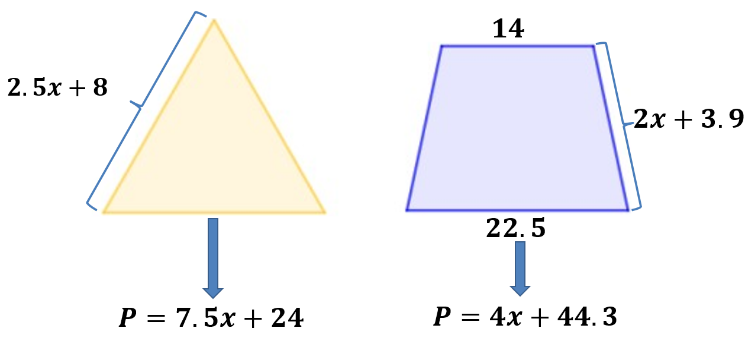
¿Qué ecuación se puede modelar con el ejemplo anterior?

Aplicando la propiedad transitiva de las ecuaciones, puedes igualar ambas expresiones, ya que la situación dice que el perímetro de ambas figuras es el mismo, por lo tanto, se establece la siguiente ecuación:

7.5x + 24 = 4x + 44.3

Resuelve la ecuación para posteriormente saber cuál es el perímetro de las dos figuras.

La situación enuncia que el perímetro del triángulo está representado por la expresión 7.5x+24 y es igual al perímetro de un trapecio, cuyo perímetro está representado por la expresión 4x+44.3.

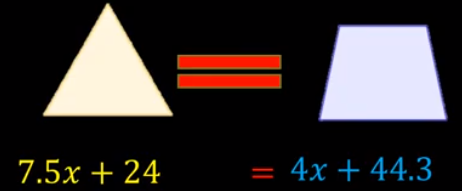
Resuelve la ecuación para determinar el valor de “x”.

Aplicando la propiedad uniforme, puedes restar 24 al primer miembro y también en el segundo, esto con la finalidad de reducir términos en el primer miembro, 7.5x + 24 -24= 0, así que no se pondrá. En el segundo miembro, 4x 44.3 - 24 es igual a 20.3.

7.5X = 4x + 20.3

Para simplificar en el segundo miembro, restas 4x en el primer miembro y 4x en el segundo miembro, reduces términos; 7.5x - 4x = 3.5x, y esto es igual a 4x - 4x =0 y sólo colocas 20.3.

3.5x = 20.3

Ahora, para despejar a “x”, divides a ambos miembros entre 3.5.

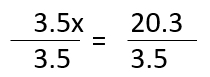
Por lo tanto:

x = 5.8

Para comprobar, colocas la ecuación original, que es 7.5x+24=4x+44.3, sustituyes el valor de “x” en la ecuación, es decir, en lugar de escribir “x”, escribes 5.8, que fue el valor que se encontró.

7.5(5.8) + 24 = 4(5.8) + 44.3

43.5 + 24 = 23.2 + 44.3

67.5 = 67.5

Se concluye que 67.5 es el perímetro del triángulo y 67.5 es el perímetro del trapecio, por lo tanto, el perímetro de las dos figuras es igual.

Ya viste que existen ecuaciones con valores decimales, pero también existen ecuaciones con valores fraccionarios.

Resolverás ahora unos ejercicios de ecuaciones del tipo ax + b = cx + d, pero con fracciones:

La ecuación 10/4x-11/4=3/4x+10/4; vas a usar las propiedades de la igualdad. La prioridad es despejar a “x” y así conocer su valor. Se empieza eliminando 11/4 negativo en el primer miembro, para ello colocas 11/4 positivo.

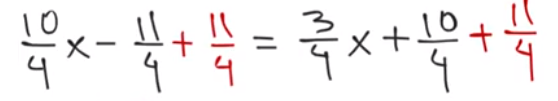
Ahora realiza las operaciones correspondientes en ambos miembros de la igualdad y así la ecuación queda:

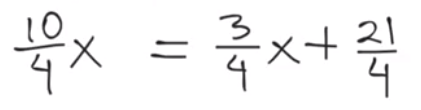
Ahora elimina 3/4 de “x” en el segundo miembro de la igualdad, para eso usaras 3/4 de “x” negativo en ambos lados, para que, al operar de lado derecho, resulte cero.

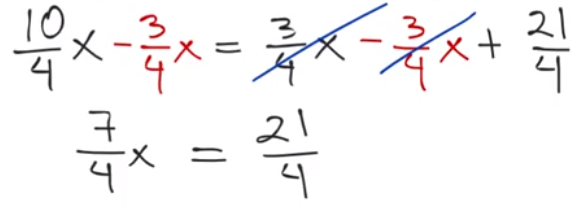
Observa que 7/4 está multiplicando a la letra “x”, ¿cómo harías para simplificarlo a 1 en una sola operación? Recuerda que ya estudiaste la propiedad del inverso multiplicativo de un número entero o fraccionario, aquí lo usarás enseguida.

Aplicando lo anterior, se tiene:

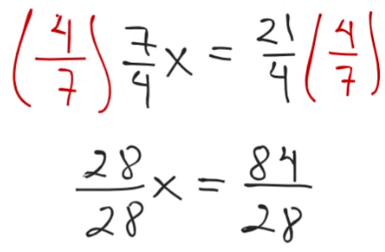
Del primer miembro tienes 28/28 es 1, que multiplica a “x”, pero no se colocará, entonces sólo será: x = 84/28. Al hacer la operación se obtiene:

X= 3

Ahora verifica que el resultado es correcto.

Ya sabes que el valor de la letra “x” es 3. Tomarás la ecuación 10/4x-11/4=3/4x+10/4, en lugar de la literal “x”, pondrás 3.

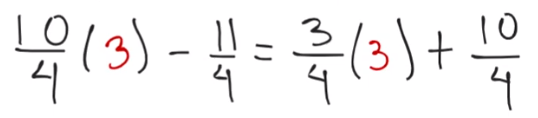
A continuación, sólo tienes que realizar las operaciones correspondientes en ambos miembros de la igualdad para verificar que, tanto de un lado como de otro, el valor sea el mismo. Entonces:

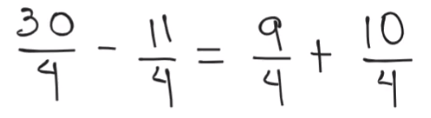
Presta atención a que en ambos miembros de la igualdad se ha reducido a dos operaciones con fracciones. Continúa resolviendo las operaciones.

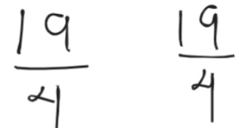
Por lo tanto, la solución es correcta, porque en ambos lados de la igualdad el resultado es el mismo.

Recuerda que una incógnita sólo puede representar ciertos valores que hagan verdadera a la igualdad.

Existirá una ecuación siempre y cuando haya una igualdad entre dos miembros, y en esta lección observaste dos tipos de ecuaciones:

ax+b=c y ax+b=cx+d

No pierdas de vista que en las ecuaciones puedes tener coeficientes y constantes en números enteros, decimales y fracciones. Asimismo, que las soluciones de estas ecuaciones pueden ser números positivos, negativos; con valores enteros, fracciones o decimales.

El Reto de Hoy:

Construye el procedimiento, conforme a lo que aprendiste en la lección, de las siguientes ecuaciones:

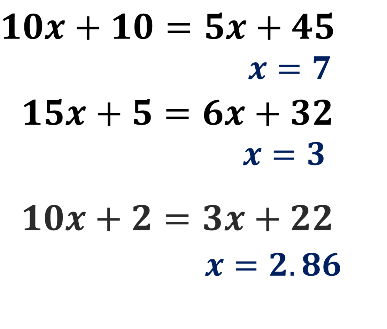
Debes poner atención en donde colocas el valor de “x” para que verifiques que lo lograste. Adicional a ello, realiza la comprobación para que te asegures de que lo hiciste bien.

Recuerda que, para resolver las ecuaciones del reto del día de hoy, debes aplicar las propiedades de la igualdad.

No olvides aplicar lo que has aprendido en las sesiones anteriores, como la ley de los signos, el inverso multiplicativo (para el caso de las fracciones) y las representaciones del lenguaje algebraico.

Revisa en el libro de texto de Matemáticas de primer grado y resuelve los ejercicios que impliquen la solución de ecuaciones de primer grado o lineales.

Descarga tu clase dando click aquí

¡Buen trabajo!

Gracias por tu esfuerzo.