Mis deportes favoritosm
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46
Mis deportes favoritos
Aprendizaje esperado: análisis del significado de la parte decimal en medidas de uso común; por ejemplo, 2.3 metros, 2.3 horas.
Énfasis: interpretar y explicar la diferencia que existe entre una unidad de medida decimal y una unidad de medida sexagesimal.
¿Qué vamos a aprender?
Interpretarás y explicarás la diferencia que existe entre una unidad de medida decimal y una unidad de medida sexagesimal.
¿Qué hacemos?
Iniciamos con nuestra clase del día de hoy, vas a conocer información relevante acerca de algunos deportes que practicamos.
Recuerda la importancia de realizar algún deporte para estar sano, por ejemplo, yo hago caminata diaria en la caminadora de mi casa, antes caminaba en el parque cercano a mi casa, pero a partir de la contingencia, lo evito.
Te quiero comentar que, desde la semana pasada, estoy registrando en unas tarjetas el tiempo que dedico para la caminata diaria, pero registré el tiempo en el sistema decimal y quiero saber a cuántos minutos equivalen en la unidad de medida sexagesimal.
Precisamente para que no se haga complicado, con este ejercicio será fácil convertir y conocer cuánto es lo que camino a diario en minutos.
Mira con ayuda de un cronómetro hice la siguiente tabla:
| Día | L | M | M | J | V | S | D |
| Tiempo recorrido | 1.3 Horas |
1.7 Horas |
1.1 Horas |
1.4 Horas |
1.2 Horas |
1.9 Horas |
1.5 Horas |
Para poder saber cuánto camino, primero necesitamos interpretar y explicar la diferencia que existe entre una unidad de medida decimal y una unidad de medida sexagesimal.
Recuerda que ya lo hicimos en la clase donde calculamos el tiempo de cada itinerario. El sistema sexagesimal se emplea como base el número 60 (sesenta), es decir, cada unidad se divide en 60 unidades de orden inferior. Se aplica en la medida del tiempo y también en la amplitud de los ángulos. Estas medidas angulares se utilizan para trazar rutas de aviones o barcos en un mapa y son el grado, minuto y segundo.
Por ejemplo: en el reloj 1 hora es igual a 60 minutos.
Precisamente para que no se te haga difícil, vamos a jugar con parejas de tarjetas con una expresión decimal (horas y fracciones decimales de horas) que son las que aparecen en mi registro y las otras expresadas en horas y minutos.
Observa las tarjetas muy bien. Después voy a sacar las tarjetas y hacer pares y te explico su relación.
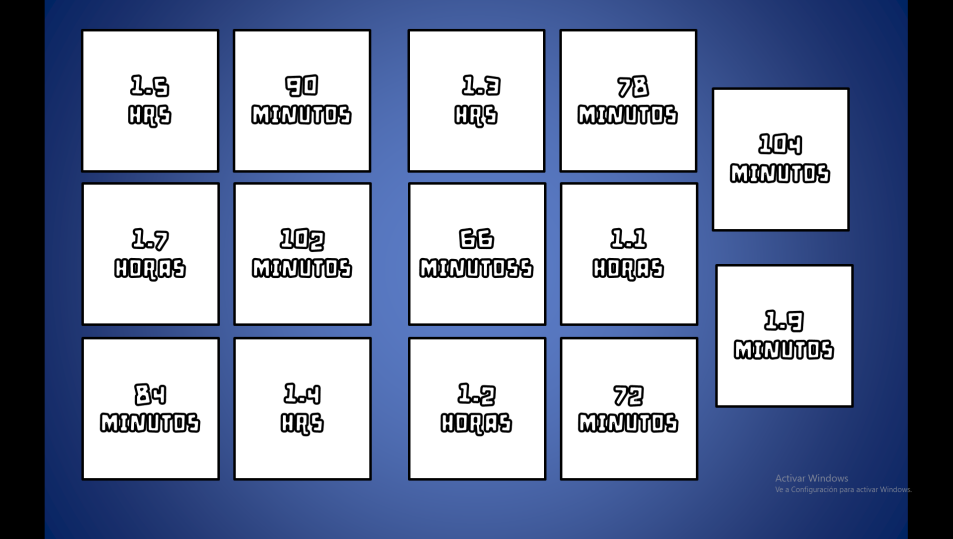
Me tocó: 1.5 horas y ahora tomo la otra que dice 90 minutos.
Porque si multiplicamos 1.5 x 60 (minutos que tiene una hora) = 90 minutos.
También podemos decir que 1 hora es igual 60 minutos más 5 décimas partes de una hora (60 minutos) que se escribe (.5 x 60) =30
Entonces sumamos 60+30 = 90 minutos.
También podemos decir que 1.5 h es igual a 1½ h que es lo mismo a 90 minutos.
Ahora me tocó: 1.7 horas y elijo otra que dice 102 minutos.
Multiplicamos 1.7 x 60 (minutos que tiene una hora) = 102 minutos.
También puede ser 60+(.7x60) =60 + 42 =102 minutos.
También puede ser de esta manera: 1 hora corresponde a 60 minutos y 0.7 corresponde a 7/10 de hora, si lo expresamos como fracción común. Ahora, debemos saber cuántos minutos es un décimo, la décima parte de una hora. ¿Cuál sería la décima parte de 60 minutos?
R = 6 minutos, ya que 6 x 10 = 60.
Entonces, si 6 minutos equivale a 1/10 de hora. ¿A cuántos minutos equivalen 7/10 de hora?
Multiplicamos 6 x 7 y nos dan 42 minutos.
Por lo tanto, 60 minutos + 42 minutos = 102 minutos.
Tengo la tarjeta con 66 minutos. La pareja es 1.1 horas.
Multiplicamos 1.1 x 60 (minutos que tiene una hora) = 66 minutos.
También puede ser 60+ (.1x60) =66 minutos.
Me tocó la tarjeta con 1.2 horas y voy a tomar la tarjeta con 72 minutos.
Porque si multiplicamos 1.2 x 60 (minutos que tiene una hora) = 72 minutos.
También puede ser 60 + (.2x60) = 60 + 12 =72 minutos.
Recuerda que también se puede hacer usando fracciones comunes.
Me tocó la tarjeta con 114 minutos y la otra tiene 1.9 horas.
Multiplicamos 1.9 x 60 (minutos que tiene una hora) = 114 minutos.
También puede ser 60+ (.9 x 60) = 60 + 54 = 114 minutos.
Me tocó 1.3 horas y tomo la otra que dice 78 minutos.
Multiplicamos 1.3 x 60 (minutos que tiene una hora) = 78 minutos.
Tengo la tarjeta con 84 minutos y la otra es 1.4 horas.
Multiplicamos 1.4 x 60 (minutos que tiene una hora) = 84 minutos.
También puede ser, 60 + (.4 x 60) = 60 + 24 = 84 minutos.
Ahora vamos a resolver un reto agregando más información a la tabla anterior.
| Día | L | M | M | J | V | S | D |
| Tiempo recorrido | 1.3 Horas |
1.7 Horas |
1.1 Horas |
1.4 Horas |
1.2 Horas |
1.9 Horas |
1.5 Horas |
| Distancia recorrida | 6.5 km |
8.5 km |
5.5 km |
7,0 km |
6.0 km |
9.5 km |
7.5 km |
Con los datos de la tabla, vamos a responder las siguientes preguntas:
- ¿Cuántos metros caminé en total, durante la semana?
- ¿Cuántos metros caminé el día jueves?
- ¿Cuántos minutos hay de diferencia entre mi caminata del día miércoles y la del domingo?
- ¿Cuántas horas y minutos caminé en total esta semana?
No es difícil, solo hay que recordar lo visto en las sesiones anteriores relacionadas con unidades de longitud y sus equivalencias.
PREGUNTA No. 1 ¿Cuántos metros caminé en total durante la semana?
R = 50,500 m.
Primero sumo los recorridos de cada uno de los días, la cual está en kilómetros.
| Día | Km. recorridos |
| L | 6.5 |
| M | 8.5 |
| Mi | 5.5 |
| J | 7.0 |
| V | 6.0 |
| S | 9.5 |
| D | 7.5 |
| TOTAL | 50.5 Km |
Después los convertí a metros, ya que esta es la pregunta, 50.5 x 1000 = 50,500 m.
Multipliqué por 1000 porque 1Km equivale a 1000 m.
PREGUNTA No. 2 ¿Cuántos metros caminé el día jueves?
R = 7000 metros.
El día jueves caminé 7 Km entonces hacemos la siguiente operación: 7 x 1000 = 7000 y la respuesta es igual a 7000 metros.
PREGUNTA No. 3 ¿Cuántos minutos de diferencia hay entre mi caminata del día miércoles y mi caminata del domingo?
R = 24 minutos.
Primero calculamos la diferencia entre 1.1 y 1.5, para saber la diferencia, restamos, 1.5-1.1 = 0.4.
Ahora que sé que la diferencia es 0.4, voy a convertirlo al sistema sexagesimal, así que debo multiplicar (.4 x 60) = 24.
También se puede obtener la respuesta convirtiendo cada uno de los tiempos mencionados en minutos.
1 x 60+ 1 x 6= 60 + 6 = 66; 1.1 h es igual a 66 minutos.
1 x 60+5 x 6= 60 + 30 = 90; 1.5 h es igual a 90 minutos.
Entonces la diferencia entre 90 y 66 = 24 minutos.
PREGUNTA No. 4 ¿Cuántas horas y minutos caminé en total esta semana?
R = 10 horas y 6 minutos.
Tenemos que sumar los tiempos de cada día, y luego convertirlos a la unidad de medida sexagesimal.
Entonces sumamos 1.3+1.7+1.1+1.4+1.2+1.9+1.5 y esto es igual a 10.1
Ahora hay que convertir 1 décimo de hora a minutos, y eso son 6 minutos, porque 6 minutos es la décima parte de 60 minutos.
Pero si lo quieres hacer con operación es (.1 x 60) = 6
El día de hoy, aprendiste a interpretar y explicar la diferencia que existe entre una unidad de medida decimal y una unidad de medida sexagesimal.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.





Login to join the discussion