La probabilidad teórica de un evento

La probabilidad teórica de un evento

Aprendizaje esperado: determina la probabilidad teórica de un evento en un experimento aleatorio.

Énfasis: introducir la noción de probabilidad teórica de un evento en un experimento aleatorio.

¿Qué vamos a aprender?

Indagarás y te introducirás en la probabilidad. Para ello, explorarás el concepto de probabilidad clásica o teórica, sus características y la noción de probabilidad teórica de un evento.

Es importante saber que la probabilidad permite tomar decisiones, incluso cuando se está jugando.

¿Qué hacemos?

Para iniciar, analiza la siguiente situación.

Situación, volados

A Isabel y Alfredo, dos estudiantes de segundo de secundaria, les gusta jugar a los volados con monedas. Isabel elige una de las caras, “águila”, mientras que Alfredo, al no tener otra opción, se quedó con “sol”.

Planteado lo anterior, entre Isabel y Alfredo, ¿quién piensas que pueda ganar?

¿Cómo es que se puede determinar?

Al lanzar una moneda al aire, sólo tienes dos opciones, es decir, dos resultados posibles: águila o sol. A todos los resultados posibles de un evento se les denomina espacio muestral.

Entonces, el espacio muestral del lanzamiento de una moneda es: águila y sol. Y si se contabiliza cuántos son, el número total de eventos o resultados posibles, son dos.

Entonces, ¿cómo puedes determinar matemáticamente lo que puede ocurrir?

Con la probabilidad, con ésta se puede determinar cuál es la posibilidad de que ocurra un evento y, con ello, saber quién tiene mayor posibilidad de ganar.

En el caso de Isabel, ella eligió águila, entonces, se considera un evento favorable del total de las posibilidades que se pueden presentar en un volado, que son dos. Esto, en términos matemáticos, se representa como 1 de dos o como 1 entre dos, o un medio.

Pero ¿qué sucede con Alfredo?

Alfredo también tiene un resultado favorable, que es “sol”, del total de resultados que pueden caer al lanzar la moneda, que son dos. Por lo tanto, Alfredo también tiene la misma probabilidad de ganar que Isabel, porque cada uno tiene un resultado favorable del total.

Reflexiona:

¿A qué evento está relacionado el que pueda ganar Isabel?

La probabilidad que tiene Isabel de ganar está relacionada con el evento de que caiga águila al lanzar una moneda; asimismo, la probabilidad de ganar para Alfredo está relacionada con el evento de que caiga sol.

La probabilidad de que caiga águila al lanzar una moneda es 1 de 2 o de un medio, y la probabilidad de que caiga sol también es de un medio. Por esta razón, se sabe que tanto Isabel como Alfredo tienen la misma probabilidad de ganar.

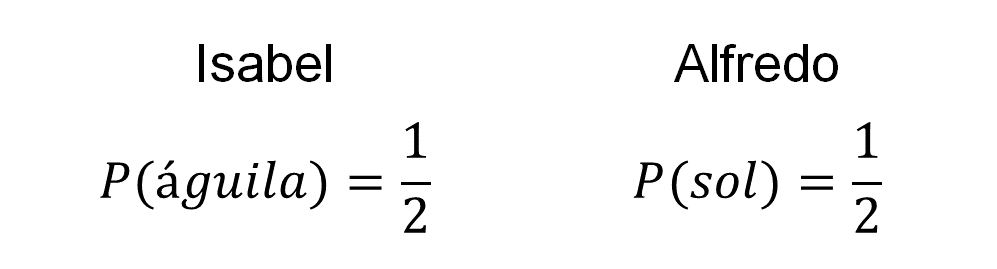
Analiza otra situación.

Situación, lanzar dados

Patricia y su hermano Antonio juegan a lanzar un dado. Cada uno debe elegir tres números diferentes de las caras del dado, sin que se pueda repetir ningún número.

En el primer juego, Patricia eligió las caras con los números 1, 4 y 6, y Antonio eligió las caras con los números restantes: 2, 3 y 5.

¿Entre ella y él, quién tiene mayor probabilidad de ganar con esa selección?

¿Cómo se puede determinar?

Cuando se lanza un dado al aire, puede caer 1, 2, 3, 4, 5 o 6, ya que es el espacio muestral para el lanzamiento de un dado, y se representa con la letra “omega” del alfabeto griego, aunque puedes encontrar en algunos textos que se representa con la letra “s”.

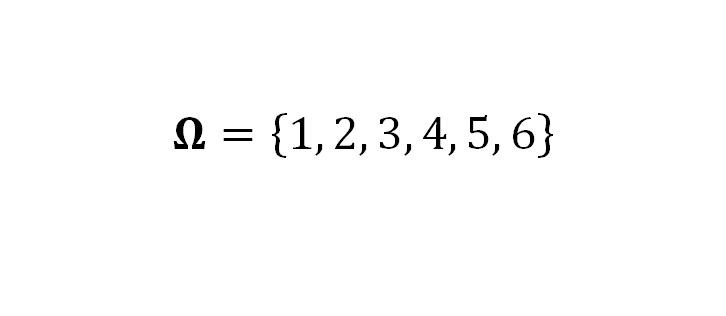
Es importante reconocer cuál es el espacio muestral cuando se propone un experimento, porque con él se realiza el conteo del número de resultados o eventos totales del experimento.

Se identifica que en total hay seis resultados o eventos posibles. Analiza:

De ellos, ¿cuántos son favorables para Patricia, que eligió las caras con los números 1, 4 y 6?

Son tres resultados favorables.

Entonces, ¿cuál es la probabilidad de que gane Patricia? Es decir, que al lanzar un dado caiga en alguna de las caras 1, 4 o 6.

Son tres resultados favorables del total de resultados o eventos posibles, que son seis; esto quiere decir que la probabilidad de que caiga 1, 4 o 6 al lanzar un dado, es de tres sextos.

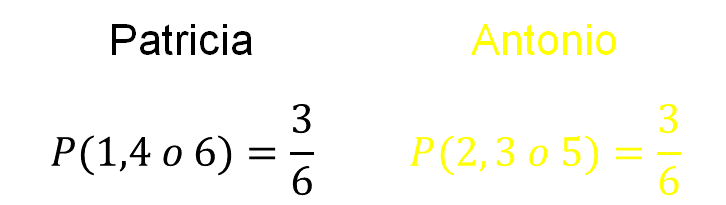
Ahora, analiza qué sucede con la selección de Antonio, quien también tiene tres resultados favorables de un total de seis.

Antonio eligió tres números del total de los posibles resultados, por lo que, la probabilidad de que caiga 2, 3 o 5 al lanzar un dado, es también de tres sextos.

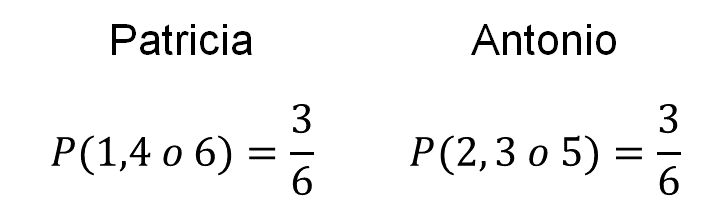
Se puede concluir que, si Patricia y Antonio eligen cada quien tres caras con números diferentes, ambos tienen la misma probabilidad de ganar, y ésta es de tres sextos o su equivalente, un medio, es decir, 0.5, que representa 50% del total de los resultados posibles.

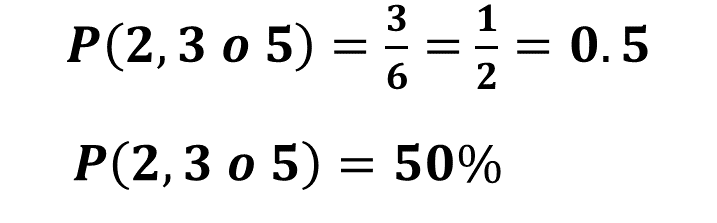
En el segundo juego Patricia elige las caras con los números 1, 3 y 5, y Antonio selecciona los números restantes: el 2, 4 y 6. Entre Patricia y Antonio, ¿quién tiene mayor probabilidad de ganar?

Analiza esta nueva situación. Patricia eligió tres resultados que son favorables de seis resultados totales posibles; entonces, la probabilidad de que al lanzar un dado caiga 1, 3 o 5, es de tres sextos, lo que equivale a un medio o cinco décimos, que representan 50% del total de los resultados posibles.

Por la misma razón, Antonio, al elegir los otros tres resultados de los seis posibles, obtiene que la probabilidad de que al lanzar un dado caiga 2, 4 o 6, sigue siendo de tres sextos, que es igual a un medio, y a su vez a 0.5, representando el otro 50% del total de los resultados posibles.

Por lo tanto, igualdad de condiciones puede dar igualdad de posibilidades. Ahora recapitula lo que has aprendido hasta este momento.

Has identificado que, al lanzar una moneda al aire, la probabilidad de que caiga sol o águila es de un medio o su equivalente, cinco décimos; es decir, hay 50% de probabilidad de que caiga sol o de que caiga águila; por esta razón, cuando dos personas juegan un volado, cualquiera de ellas tiene la misma probabilidad de ganar, aunque no efectúen el volado.

También analizaste que, al lanzar un dado, la probabilidad de que caiga 1, 3 o 5 es igual a la probabilidad de que caiga 2, 4 o 6, porque los resultados favorables, en cada caso, representan la mitad de los eventos totales. Por lo tanto, la probabilidad de que caiga 1, 3 o 5 es de tres sextos, igual a un medio o su equivalente de 0.5, representando 50% del total de los resultados posibles. Esto mismo ocurre cuando se calcula la probabilidad de obtener 2, 4 o 6.

Ahora, analiza otra situación.

Situación, ruleta

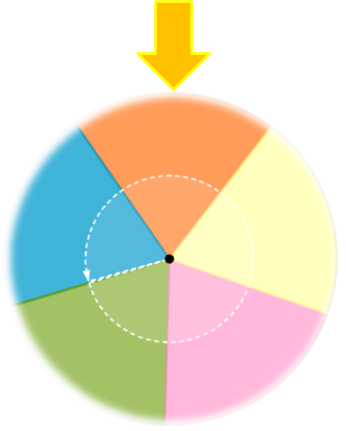
Una ruleta está dividida en cinco sectores circulares iguales, como se muestra en la siguiente imagen.

¿Cuál es la probabilidad de que al girar la ruleta el color naranja quede señalado con la flecha?

Al preguntar esto a tres estudiantes de segundo grado de secundaria, respondieron lo siguiente.

• Lucía mencionó que la probabilidad de que quede señalado el color naranja es uno de cinco.
• Rafael contestó que la probabilidad de que quede señalado el color naranja es de 20%.
• Y Sonia respondió que utilizó el ángulo central de 72 grados y lo dividió entre 360 grados.

Analiza cada uno de los razonamientos y verifica, ¿quién está en lo correcto?

Lucía mencionó que la probabilidad de que quede señalado el color naranja es uno de cinco, porque el área que representa el color naranja es una, parte de un total de cinco partes iguales.

Rafael, por su parte, contestó que es 20%, porque si 100% es todo el círculo, la quinta parte que tiene el color naranja representa 20%.

Mientras que Sonia utilizó el ángulo central del sector circular naranja; para ello, dividió 360 grados entre cinco partes iguales, obteniendo 72 grados. Posteriormente dividió 72 grados del ángulo central del sector naranja entre el total, que son 360 grados, y esto equivale a un quinto.

Eso significa que Lucía, Rafael y Sonia están en lo correcto.

El sector circular naranja representa la quinta parte del círculo, es decir, una parte de un total de cinco que lo componen. Por ello, la probabilidad de que quede señalado por la flecha el sector de color naranja intrínsecamente es un quinto, que a su vez representa 20% del total del círculo.

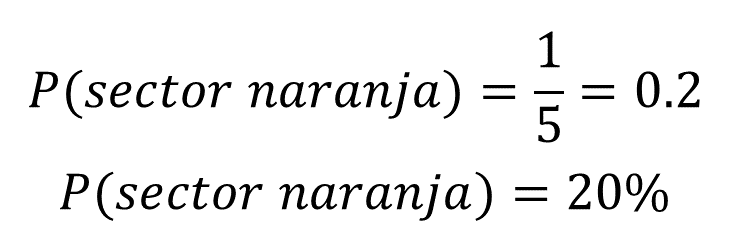
Con lo que has desarrollado, ya puedes contestar las siguientes preguntas:

¿Cuál es la probabilidad de que, al girar la ruleta, quede señalado el color verde? y ¿cuál es la probabilidad de que, al girar la ruleta, quede señalado el color rosa?

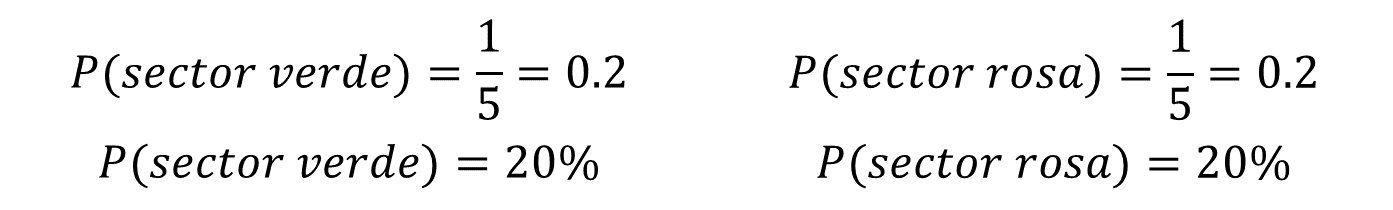
Puedes visualizar que la probabilidad de que quede señalado el color verde es igual a la que se obtuvo para el color naranja, ya que al tratarse de sectores que representan la quinta parte del círculo, la probabilidad de ocurrir es de 20%.

De la misma forma, la probabilidad de que al girar la ruleta quede señalado el color rosa, es de 20%.

Pero ¿qué ocurre cuando los sectores circulares no tienen áreas iguales?, ¿cuál es la probabilidad de que al girar la ruleta caiga en cualquiera de esos sectores circulares?

Analiza la siguiente imagen para que puedas responder a las preguntas.

A simple vista, ¿cuál de los sectores circulares consideras que tiene mayor probabilidad de quedar señalado? y ¿por qué?

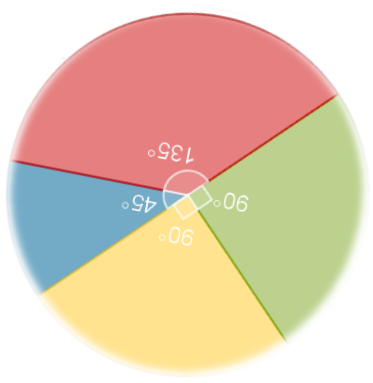
Como el área de cada sector es proporcional al ángulo central que lo forma, el sector rojo es el que tiene mayor probabilidad de quedar señalado, porque al compararlo con ángulos centrales de los otros sectores, el rojo es el de mayor amplitud.

Para calcular la probabilidad de cualquiera de los sectores circulares, basta con establecer las relaciones entre el ángulo central que forma cada uno de ellos con el ángulo total que conforma el círculo, que es de 360 grados.

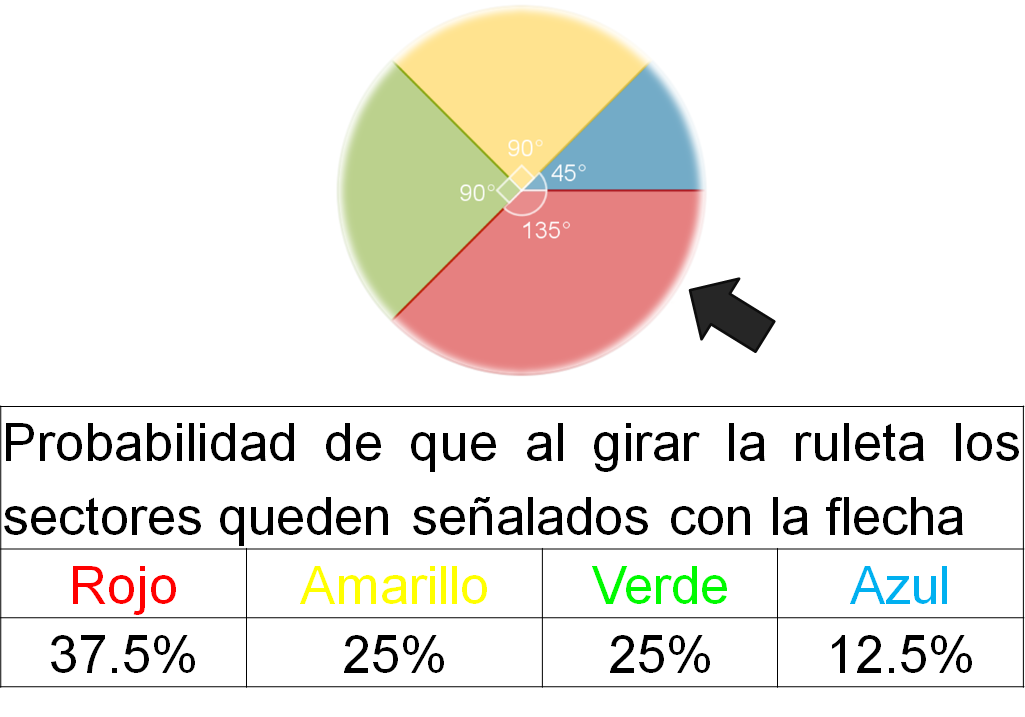
Probabilidad de que al girar la ruleta quede señalado el sector rojo:

Probabilidad de que al girar la ruleta quede señalado el sector amarillo:

Probabilidad de que al girar la ruleta quede señalado el sector verde:

Probabilidad de que al girar la ruleta quede señalado el sector azul:

Al comparar las probabilidades de que al girar la ruleta quede señalado alguno de estos sectores, se corrobora que el sector con color rojo es mayor que cualquier otro sector, por ello, se dice que hay mayor probabilidad de que ocurra ese evento. También se puede concluir que el sector que tiene menor probabilidad de quedar señalado es el azul.

Entonces, ¿cómo puedes obtener la probabilidad de cualquier evento al proponer un experimento aleatorio?

Reflexiona detenidamente en todas las situaciones que has analizado hasta este momento.

¿Te has dado cuenta de que no se ha realizado ningún experimento?

No has lanzado al aire una moneda ni un dado y tampoco has girado la ruleta; sin embargo, puedes obtener la probabilidad de un evento, como el obtener un águila al lanzar una moneda o que al lanzar un dado caiga un número par, o que al girar una ruleta quede señalado cierto sector circular sin haber realizado los experimentos.

A este tipo de probabilidad en la que no se realizan los experimentos, pero se consideran las características de los eventos, se le denomina probabilidad clásica o teórica.

Y es clásica por la consideración de que todos los eventos tienen la misma ponderación previa a la experimentación, en contra de la frecuencial, cuyos valores provienen de un experimento y, por lo tanto, varían.

A continuación, realiza lo siguiente:

Construye y escribe con tus palabras la definición de la probabilidad clásica o teórica. Revisa tu libro y compara tu definición con la incluida en éste.

Es importante saber que la probabilidad permite tomar decisiones, incluso cuando se está jugando.

Ahora, resuelve el siguiente ejercicio.

Situación, moneda y dado al aire

Al lanzar una moneda y un dado al aire al mismo tiempo…

• ¿Cuál es la probabilidad teórica de que caigan sol y número par?
• ¿Cuál es la probabilidad teórica de que caigan águila y un múltiplo de 3?
• ¿Cuál es la probabilidad teórica de que caigan sol y el número 5?
• ¿Cuál es la probabilidad teórica de que caigan águila y un número mayor a 4?
• ¿Cuál es la probabilidad teórica de que caigan sol y un número menor o igual a 4?

Para resolver este ejercicio, primero identifica el espacio muestral: lo harás en una tabla o en un cuadro de doble entrada, aunque también puedes obtener el espacio muestral con un diagrama de árbol.

El número total de eventos son: seis, que corresponden al águila de la moneda, combinada con el 1, 2, 3, 4, 5 y 6 del dado, y otros seis, que corresponden al sol de la moneda, con el 1, 2 ,3 ,4, 5 y 6 del dado. Entonces, el número total de eventos son 12.

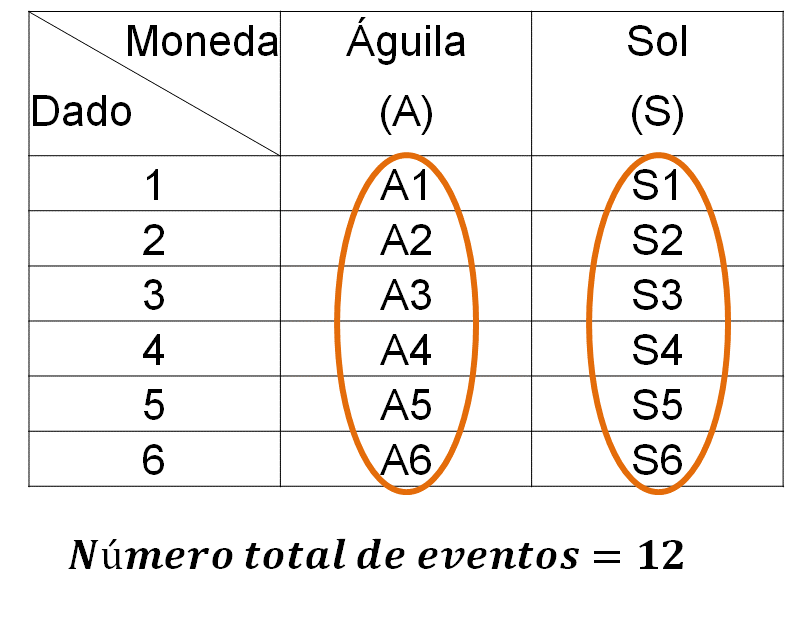
Con el número total de eventos, puedes obtener la probabilidad de cualquiera de los eventos planteados en el ejercicio.

Primera pregunta:

Para determinar… ¿cuál es la probabilidad teórica de que caigan sol y número par?

Identifica los eventos favorables en el cuadro, que son: sol-2, sol-4 y sol-6, por lo tanto, el número de eventos favorables es 3, y el número total de eventos es 12. Como la probabilidad teórica “P” de que ocurra un evento “e” es el número de eventos favorables entre el número total de eventos, tienes que la probabilidad teórica de que caiga sol y número par es tres doceavos, que equivalen a un cuarto o veinticinco centésimos, correspondiente a 25 por ciento del total de resultados.

Por lo tanto, es necesario identificar cuáles son los eventos favorables en el espacio muestral y cuántos son.

Segunda pregunta:

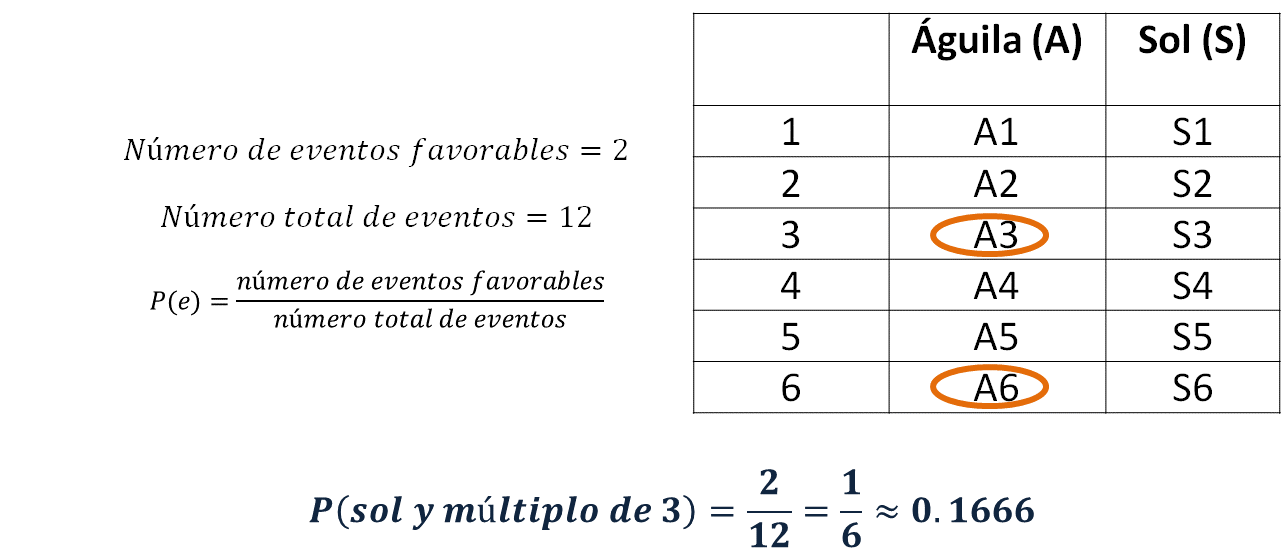
Para determinar, ¿cuál es la probabilidad teórica de que caigan águila y un múltiplo de 3?

Como los múltiplos de tres que aparecen en el dado son tres y seis, los eventos favorables que se identifican en el cuadro son: águila-3 y águila-6, es decir, el número de eventos favorables es dos, mientras que el número total de eventos son doce. Como la probabilidad teórica “P” de que ocurra un evento “e” indica el número de eventos favorables entre el número total de eventos, entonces, la probabilidad de que caigan águila y un múltiplo de tres es igual a 2 entre doce, y simplificándolo se obtiene un sexto. Esto quiere decir que existe una probabilidad de aproximadamente 16.66% de que, al lanzar una moneda y un dado, caigan águila y un múltiplo de 3.

Pregunta 3:

Para determinar, ¿cuál es la probabilidad teórica de que caigan sol y el número 5?

Identifica en el espacio muestral, que está contenido en el cuadro, que el número de eventos favorables es sólo uno (el sol-5), y el número total de eventos sigue siendo 12. Entonces, la probabilidad de que caiga sol y el número 5, es un doceavo. Esto implica que aproximadamente existe 8.33 por ciento de probabilidad de que, al lanzar una moneda y un dado, caigan sol y el número 5.

Pregunta 4:

Para determinar, ¿cuál es la probabilidad teórica de que caigan águila y un número mayor a 4?

Lo primero es reconocer los números mayores a 4 que están en el dado, éstos son 5 y 6. Entonces, en el cuadro donde se encuentra el espacio muestral se identifica que los eventos favorables son: águila-5 y águila-6; por lo tanto, se tiene que el número de eventos favorables es 2, y como el número total de eventos es 12, la probabilidad de que caiga águila y 5 o 6 es dos doceavos o su equivalente, un sexto.

Finalmente, la pregunta 5:

Para determinar, ¿cuál es la probabilidad teórica de que caigan sol y un número menor o igual a 4?

Primero establece cuáles son los números menores o iguales a 4 que se encuentran en el dado, éstos son 4, 3, 2 y 1. Después, identifica en la tabla aquellos en los que además caiga sol, éstos son: sol-1, sol-2, sol-3 y sol-4; por ello, los eventos favorables son 4, y como el número total de eventos es de 12, entonces la probabilidad de que caiga sol y 1, 2, 3 o 4 es de cuatro doceavos o su equivalente, un tercio, que expresado en porcentaje representa, aproximadamente, 33.33 por ciento de probabilidad de que caigan sol y 1, 2, 3 o 4.

Has contestado todas las preguntas con el apoyo del maestro Eduardo, usando la definición de probabilidad teórica de un evento.

Es muy importante identificar el espacio muestral, ya que con él puedes reconocer cuáles y cuántos son los eventos totales, y esto permite determinar la probabilidad teórica.

El reto de hoy:

Analiza y resuelve las siguientes situaciones-problema:

Situación-problema, Dados con número par y múltiplos de tres

Patricia y su hermano Antonio juegan a lanzar un dado. Patricia elige las caras con número par, es decir, 2, 4 y 6; mientras que Antonio seleccionó aquellas caras que tienen múltiplos de tres, es decir, 3 y 6.

Determina: ¿quién de ellos tiene mayor probabilidad de ganar? y ¿por qué?

Para contestar las preguntas anteriores, te puedes guiar resolviendo los siguientes cuestionamientos:

¿Cuál es la probabilidad de que al lanzar un dado caiga número par? y ¿cuál es la probabilidad de que al lanzar un dado caiga un múltiplo de tres?

Situación-problema, mismo número o suma 7

Rosa dice que tiene mayor probabilidad de ganar si al lanzar dos dados elige que en ambos caerá el mismo número, que si elige que la suma de sus caras sea de 7. ¿Estás de acuerdo con ella? Argumenta tu respuesta.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/