Números decimales

Aprendizaje esperado: Lectura, escritura y comparación de números naturales, fraccionarios y decimales. Explicitación de los criterios de comparación.

Énfasis: Reflexionar sobre el criterio de: “A mayor número de cifras decimales, más grande es el número”.

¿Qué vamos a aprender?

Aprenderás a reflexionar sobre el criterio de: A mayor número de cifras decimales, más grande es el número, a través de la lectura, escritura y comparación de números naturales, fraccionarios y decimales.

Para explorar más puedes revisar el libro de texto de Desafíos matemáticos de 6º se explica el tema a partir de la página 13

https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/13

¿Qué hacemos?

A continuación, te presentamos información y algunas actividades que te ayudarán a profundizar en tu conocimiento y comprensión sobre los números decimales.

En la clase de hoy comenzaremos a resolver el desafío 4 del libro de Desafíos matemáticos para sexto grado, denominado, ¿Qué pasa después del punto? El propósito es comprobar si un número decimal con mayor número de cifras es mayor o menor que otro número decimal con menos cifras; para ello, vamos a recordar cómo se leen los números decimales y los compararemos para determinar qué número es mayor.

¿Recuerdas qué tipos de números usamos en el Desafío 1 “Los continentes en los números”, y en el Desafío 2 “Sin pararse”?

En el Desafío 3 “Carreras de robots”, viste números fraccionarios, pero todavía te faltan otros tipos de números por conocer. Hoy, por ejemplo, vamos a estudiar con otros números que ya hemos visto en ciclos escolares anteriores: los números “decimales”.

Antes de empezar con el desafío aclaremos algunos puntos relacionados con los números decimales. Un número decimal es la expresión de un número no entero que tiene una parte decimal.

“El número entero y la parte decimal se separan por un punto; el entero se escribe a la izquierda del punto, y la parte decimal a la derecha del punto”.

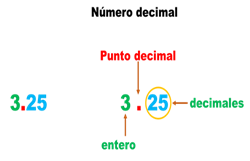
“El número que está en verde es entero, luego tenemos el punto decimal y, al final, el número en azul corresponde a los números decimales”.

“Cuando un número decimal no tiene parte entera, se coloca un cero a la izquierda del punto”.

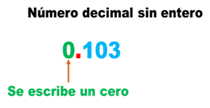
A las cifras de los decimales se les llama subórdenes.

Las cifras que forman el número decimal tienen un valor que depende del lugar del suborden que ocupen.

Cuando hablamos de décimos, nos referimos a un entero que ha sido dividido en 10 partes iguales, los décimos constituyen el primer suborden.

Si son centésimos, el entero se ha dividido en cien partes iguales y forman el segundo suborden.

Si son milésimos, se ha dividido en mil partes iguales, forman el tercer suborden, y así sucesivamente.

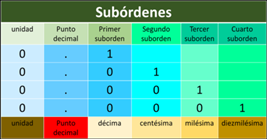
Los décimos constituyen el primer suborden, los centésimos el segundo suborden, los milésimos el tercer suborden y, por lo tanto, ¿A qué corresponde el cuarto suborden?

Los números decimales se leen de la siguiente manera:

“Cuando se lee un número decimal usando los valores posicionales se debe mencionar primero la parte entera, luego la parte decimal, en su totalidad, diciendo las partes más pequeñas que contiene el número, por ejemplo, el número 54.006 se lee así: cincuenta y cuatro enteros seis milésimas ; el número 27.583 veintisiete enteros quinientos ochenta y tres milésimas ; el número 34.0098 treinta y cuatro enteros, noventa y ocho diezmilésimas ; y, por último, el número 9,846.02202524 nueve mil ochocientos cuarenta y seis enteros, dos millones doscientos dos mil quinientas veinticuatro cien millonésimas .

¿Cómo podemos comparar números decimales?

Una forma es ir comparando decimal por decimal, iniciando por los décimos. Quien tenga la cifra mayor en los décimos, será el mayor. Si tienen igual cantidad en los décimos, comparas los centésimos. Si también son iguales, comparas milésimos, y así sucesivamente.

Por ejemplo, si tomas una tira de cartón que mide 1 metro, ese es tu entero, esta tira que resulta de dividir en 10 partes iguales a nuestro entero, ¿Qué fracción representa del entero?

Si tienes una calculadora puedes dividir 1 entre 10

Si divides 1 entre cien, ¿Qué resulta?

Ahora si tomamos la tira de 50 centímetros, ¿Esto qué parte de la tira grande es? eso ¿Cómo podemos representarlo en número fraccionario y en número decimal?

El Reto de Hoy:

Completar la siguiente tabla. No puedes escribir en las casillas sombreadas y la suma de los números que escribas en las otras casillas de cada renglón te debe dar el número de la primera columna.

Número	Unidades	Décimos	Centésimos	Milésimos
0.6
1.8
3.2
5.12

Si en tu casa hay otros libros relacionados con el tema, consúltalos, así podrás saber más, si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.

También te recomendamos explorar el Cuaderno de Trabajo para el estudiante “Vamos de Regreso a Clases”

https://educacionbasica.sep.gob.mx/multimedia/RSC/BASICA/Documento/202008/202008-RSC-d9F6pLUg19-6.odePrimariaEstudiantesVF.pdf

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.