Ángulos y polígonos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06
Ángulos y polígonos
Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: examinar las relaciones entre las medidas de los ángulos interior, exterior y central de polígonos regulares.
¿Qué vamos a aprender?
Examinarás y determinaras los ángulos interior, exterior y central de polígonos regulares y la relación que existe entre ellos.
Lleva un registro de las ideas principales, preguntas y reflexiones que surjan durante el desarrollo de la sesión.
¿Qué hacemos?
Analiza la siguiente situación.
Se desea construir dentro de un centro de rehabilitación infantil y juvenil cuatro áreas especializadas para este fin:
La primera estará destinada para que las niñas, los niños y jóvenes hagan ejercicio en una bicicleta dentro de una alberca.
La segunda es para ejercitarse en una caminadora dentro de otra alberca.
La tercera está destinada para ayudarles a caminar en una banda con sensores de movimiento y detectar los músculos o articulaciones que deben fortalecerse.
Y la cuarta, para obtener flexibilidad en todo el cuerpo con la ayuda de ejercicios con un balón.

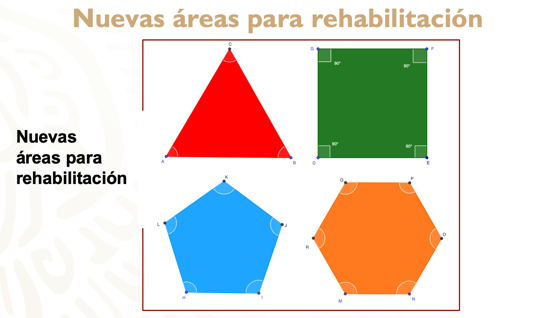
Lo que se pretende es que estas áreas tengan formas de polígonos regulares diferentes.
¿Recuerdas qué es un polígono regular?
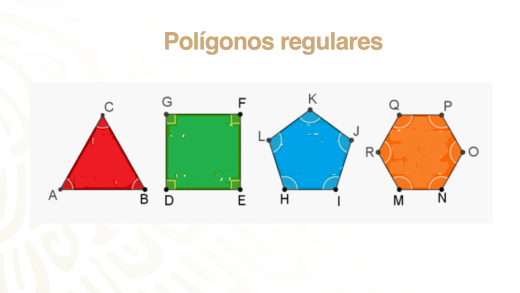
Los primeros cuatro polígonos regulares son: el triángulo equilátero, el cuadrado, el pentágono regular y el hexágono regular.
El triángulo equilátero.
¿Qué características tiene un triángulo equilátero y en qué es diferente de un escaleno o un isósceles?
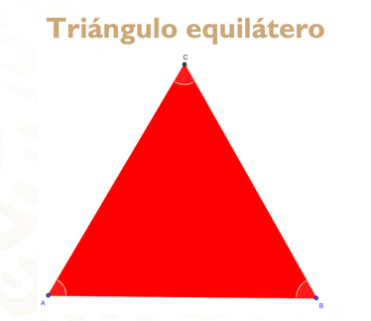
En el triángulo equilátero los tres lados son iguales, es decir, tienen la misma longitud.
Analiza ahora el segundo polígono regular, el cuadrado.
Como ya sabes, éste tiene cuatro lados iguales; ahora observa sus ángulos interiores, ¿cómo son?
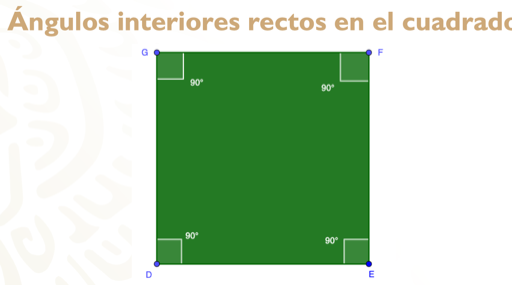
Son iguales o congruentes y miden 90 grados, es decir, son ángulos rectos.
Entonces diremos que, para que un polígono sea regular, debe cumplir con dos condiciones, que sus lados y sus ángulos interiores sean iguales.
Esto también ocurre en el pentágono y en el hexágono regulares: sus lados y ángulos interiores son iguales.
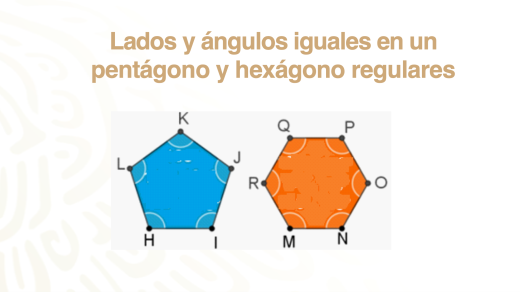
Date tiempo para revisarlos y trazarlos en tu cuaderno.
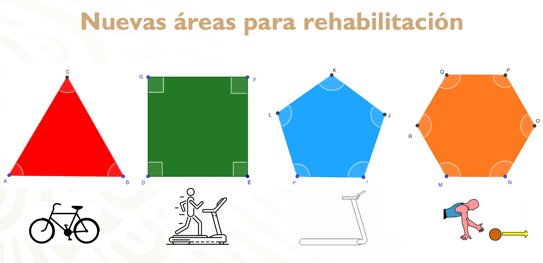
Ya que sabes cuáles son algunas características de los polígonos regulares, puedes proponerlo como modelo para tu construcción en las nuevas áreas de especialidad en el centro de rehabilitación de niñas, niños y jóvenes. ¿Cómo los asignarías?
- El triángulo para la alberca con bicicleta sumergible.
- El cuadrado para la alberca con caminadora sumergible.
- El pentágono regular para la banda caminadora sobre piso.
- Y el hexágono regular para el ejercicio con balón en piso.
Hemos hablado de los ángulos interiores de los polígonos regulares, pero ¿qué características tienen estos ángulos?, ¿y qué otros ángulos se puedes identificar en los polígonos regulares además de los ángulos interiores?
Recuerda anotar las preguntas que se plantean para darles seguimiento y respuesta a lo largo de la clase.
Recupera los conceptos más relevanates de lo has revisado hasta ahora.
Has visto que los polígonos regulares tienen lados y ángulos interiores iguales y de los ángulos interiores de esos polígonos.
Ahora, aprenderás cómo calcular los ángulos interiores de cualquier polígono regular y, a partir de este conocimiento, poder definirlo. Ya sabes que los ángulos interiores de los polígonos regulares son iguales, pero ¿cómo podemos calcularlos dependiendo el tipo de polígono del que se trate?
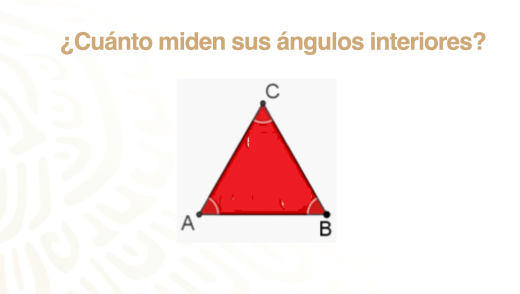
Comienza con el triángulo equilátero.
¿Cuánto miden sus ángulos interiores?
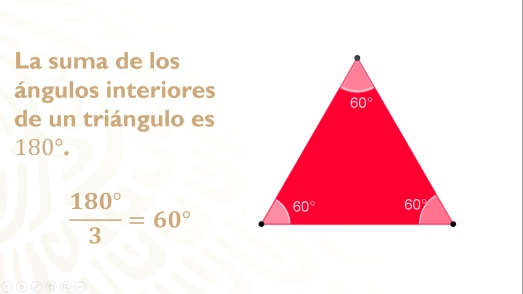
Partiremos de un hecho que ya conoces muy bien: “La suma de los ángulos interiores de un triángulo es igual a 180 grados”.
Por lo tanto, como los tres ángulos interiores son iguales, dividimos 180 entre 3 y el resultado es 60 grados por ángulo.
Observa que los tres ángulos interiores son iguales y tienen un valor de 60°.
De hecho, en cualquier triángulo construible o existente se cumple que la suma de sus ángulos interiores es 180 grados.
Aprovecharemos esta característica para determinar la medida de los ángulos interiores de los demás polígonos regulares.
Considerando que ya sabes trazar las diagonales en un polígono desde uno de sus vértices, identifica cuántos triángulos se forman dentro de cada uno de los siguientes polígonos regulares.
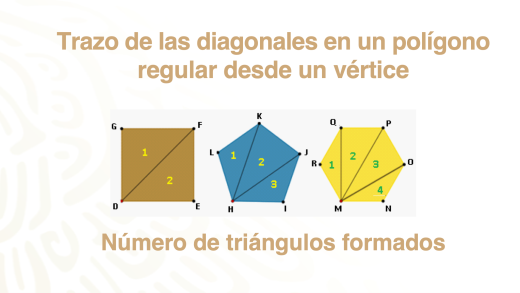
- En el cuadrado se forman 2.
- En el pentágono regular se forman 3.
- En el hexágono regular se forman 4.
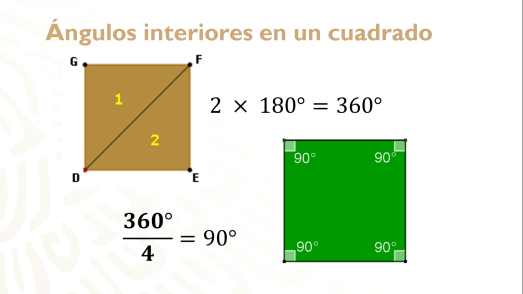
En el cuadrado, la suma de los ángulos interiores es igual al número de triángulos formados en su interior, que son 2 por 180°, esto es, 360°; ahora sólo divides esta suma entre los 4 lados y el resultado es 90°.
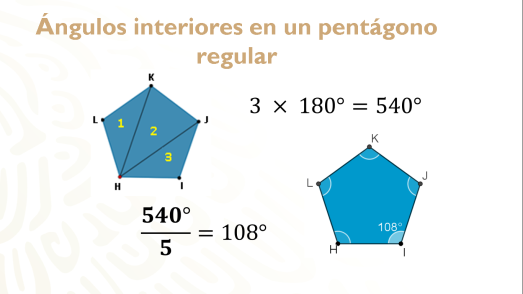
En el caso del pentágono regular, se formaron en su interior 3 triángulos, entonces, la suma de sus ángulos es equivalente a 3 por 180 grados igual a 540°. Ahora, dividiendo esta suma entre 5 lados, tienes que cada ángulo interior es de 108°. Entonces, el ángulo interior de un pentágono regular es de 108°.
Finalmente, en el hexágono regular se formaron 4 triángulos en su interior, entonces, 4 por 180° es igual a 720°, y 720° entre 6 lados es igual a 120°. El ángulo interior en un hexágono regular es de 120°.
¿Qué pasa si sigues este procedimiento con otros polígonos regulares?
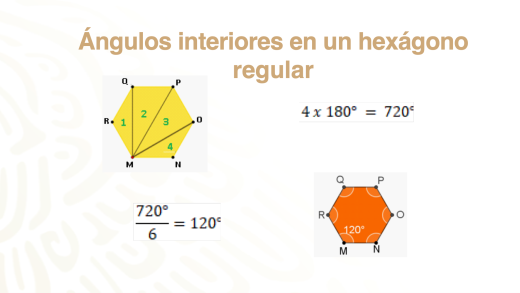
Podrías calcular el valor de los ángulos interiores de cualquier polígono regular.
Para encontrar una fórmula o una generalización que te diga cómo calcular el ángulo interior de cualquier polígono, recurre a una tabla y examina su contenido para después encontrar o modelar una expresión general.
En la tabla llena la columna del número de lados de cada polígono regular después completa la columna del número de triángulos que se forman, en la siguiente columna multiplica el número de triángulos por 180° para encontrar la suma de los ángulos interiores de cada polígono y, para encontrar el valor del ángulo interior, simplemente divide esta suma entre el número de lados.
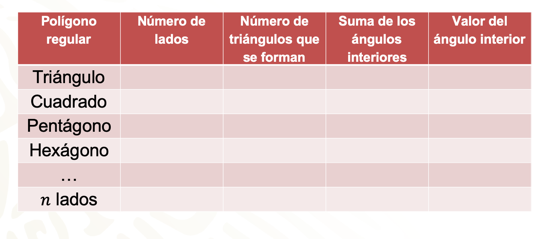
Recopila la información que has analizado y completa la tabla.
Para un triángulo, el número de lados es 3, para un cuadrado es 4, para un pentágono es 5, en un hexágono son 6, y así sucesivamente.
Ahora completa la tercera columna. El número de triángulos que se forman en un triángulo es uno, en un cuadrado son 2, para un pentágono son 3, en un hexágono son 4, y así sucesivamente.
En la cuarta columna, como ya lo has analizado, la suma de los ángulos interiores de un polígono depende del número de triángulos. En un triángulo la suma de los ángulos interiores es uno por 180 grados, es decir, 180 grados. En un cuadrado tienes 2 por 180 grados, esto es, 360 grados. Para un pentágono es 3 por 180 grados, igual a 540 grados. En un hexágono son 4 por 180 grados, igual a 720 grados, y así sucesivamente.
Para obtener la amplitud de cada ángulo interior, basta con dividir la suma de los ángulos interiores del polígono entre el número de lados. De esta forma, para un triángulo equilátero, divide 180 grados entre 3 y obtendrás que cada uno de los ángulos interiores tiene una amplitud de 60 grados.
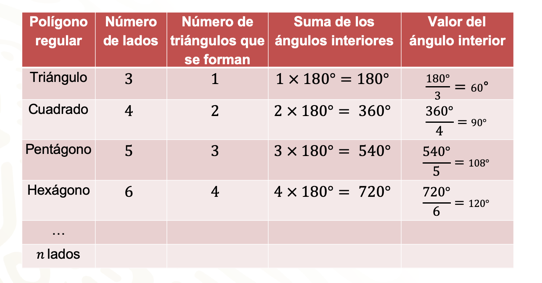
De forma análoga, cada uno de los ángulos interiores del cuadrado se obtiene al dividir 360 grados entre 4, esto es, 90 grados. En un pentágono, es 540 grados entre 5, igual a 108 grados. Para el hexágono son 720 grados entre 6, igual a 120 grados.
¿Qué pasa si sigues así?
Llegarás a un polígono regular de ene lados, el cual colocas en la primera columna en la tabla que tendrá n lados, dato que colocas en la segunda columna, y se formarán n-2 triángulos en su interior, información que llenas en la tercera columna, y que, multiplicados por 180 grados, te darán la suma de ángulos interiores que colocarás en la cuarta columna, y finalmente divides ésta entre el número de lados, que es “ene”, para determinar así el ángulo interior de un polígono de n lados.
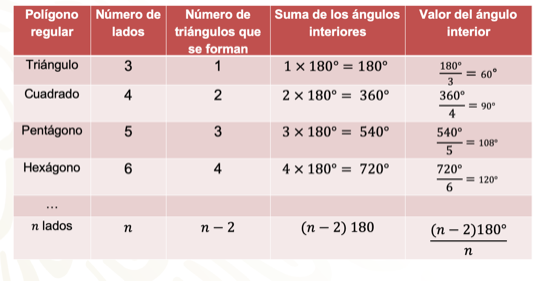
Como puedes notar, has construido una fórmula que te indica cómo calcular el ángulo interior de cualquier polígono regular: n -2 por 180 grados entre n, en donde ene representa el número de lados del polígono.

Hasta ahora has aprendido cómo calcular o determinar el ángulo interior de un polígono regular, pero ¿qué es el ángulo interior?
¿Cómo puedes definirlo después de haber trabajado con él?
Analízalo e identifica el ángulo interior en un hexágono regular.
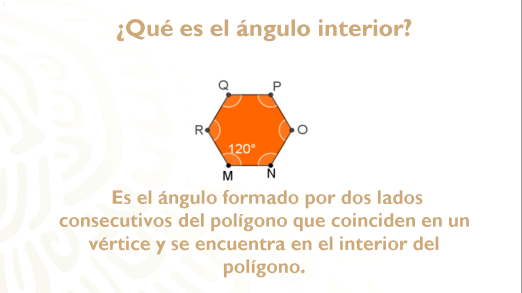
Ahora observa que el ángulo se forma entre dos lados consecutivos del polígono. Puedes entonces decir que: “El ángulo interior de un polígono regular es el que está formado por dos lados consecutivos de éste”.
Esto quiere decir que tienen un vértice en común y, además, este ángulo se encuentra dentro del polígono.
Ahora vas a identificar otros ángulos relacionados con el ángulo interior de un polígono regular.
¿Sabes cómo se llaman los otros ángulos que pueden identificarse en un polígono regular?
Observa el siguiente pentágono regular y uno de sus ángulos interiores.
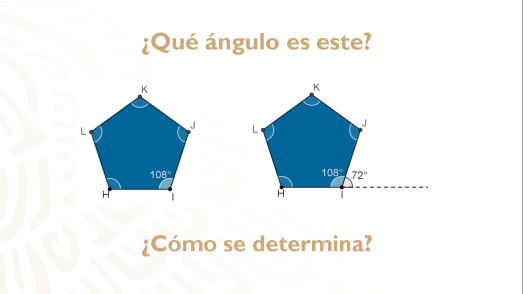
Ahora prolonga uno de sus lados, el adyacente a su ángulo interior.
Se forma un ángulo.
¿Qué ángulo es este?
¿Cómo puedes determinarlo?
¿Cómo se llama ese ángulo?

Una forma de conocerlo es midiéndolo con un transportador. Y vemos que mide aproximadamente 72 grados, decimos aproximadamente, porque podemos cometer un error de medición. A este ángulo lo llamaremos ángulo exterior.
¿Cómo podrías definirlo?
¿Qué características tiene?
Examina el ángulo exterior del pentágono regular, ¿cómo lo definirías?
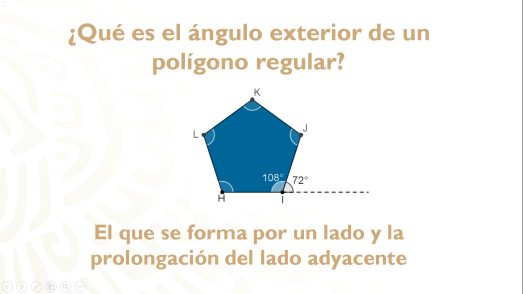
El ángulo exterior de un polígono regular es el que se forma por uno de sus lados y la prolongación del lado adyacente.
Entonces, el ángulo exterior de un pentágono regular es de 72 grados, de acuerdo con la medición que hiciste.
Y todos los ángulos exteriores del pentágono regular son iguales.
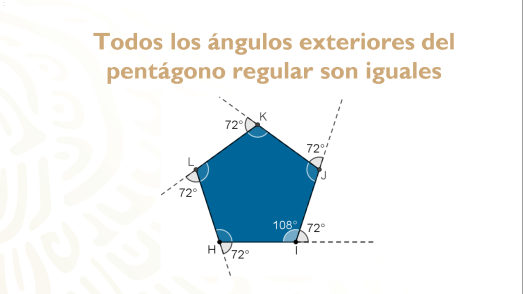
Pero ¿cómo obtienes el ángulo exterior de cualquier polígono regular sin medirlo?
Para el caso del pentágono regular, observa el ángulo interior y el exterior.
¿Cuántos grados suman los ángulos interior y exterior?
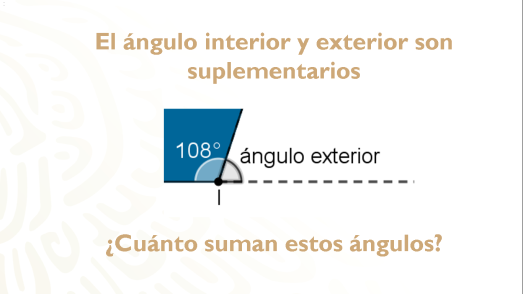
Correcto, 180°. El ángulo interior más el ángulo exterior es igual a 180 grados.
Ya tienes una expresión que relaciona el ángulo exterior con el ángulo interior.
Entonces, para todo polígono regular se tiene que: El ángulo exterior es igual a 180 grados menos el ángulo interior.
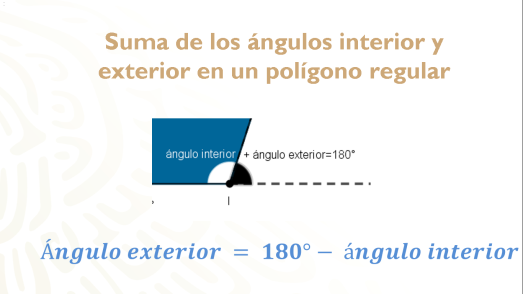
Así, para el pentágono tenemos que:
El ángulo exterior es: 180° menos 108°, igual a 72°, que corresponde al ángulo que habíamos medido.
¿Piensas que esta es la única forma de determinar el ángulo exterior de un polígono regular?

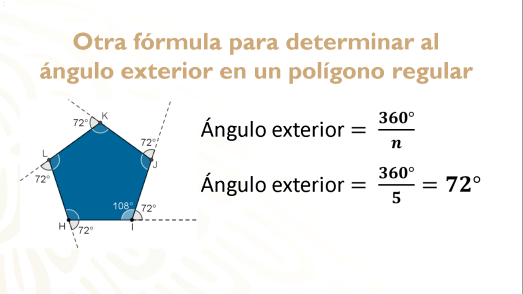
Analiza la siguiente situación: ¿cuánto suman los ángulos exteriores de un polígono?
En el caso del pentágono, son 72° por 5, igual a 360 grados.
Entonces, otra fórmula que encontrarás para determinar el ángulo exterior es dividir 360 grados entre el número de lados.
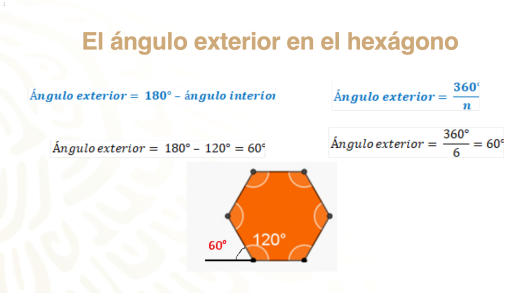
Practica con el hexágono regular, ¿qué valor tiene su ángulo exterior?
Para obtenerlo, aplica la fórmula que obtuvimos primero, la del ángulo suplementario: 180 grados menos 120 grados es igual a 60 grados.
Y con la otra fórmula, 360 grados entre 6 es igual a 60 grados.
Con ambos procedimientos obtienes el mismo resultado.
Ahora, con estas fórmulas, puedes determinar el ángulo exterior de cualquier polígono regular.
Continua con el otro ángulo que puedes identificar en un polígono regular.
¿Recuerdas la situación del centro de rehabilitación infantil y juvenil?
La bicicleta sumergible para la rehabilitación de niñas, niños y jóvenes, que se encuentra en la alberca que se instaló en un área con forma de triángulo equilátero, y tiene ruedas con seis rayos.
Y un niño la observa y se pregunta: ¿cuál será el ángulo entre los rayos de la bicicleta?
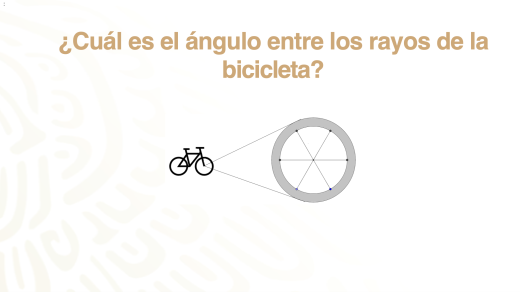
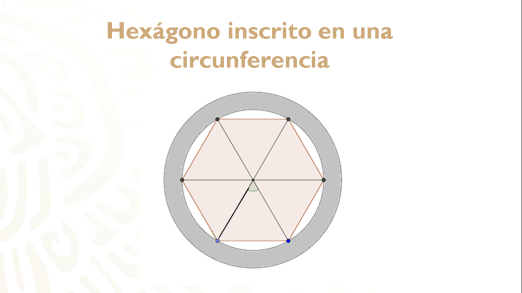
Para responder su pregunta, puedes hacer lo siguiente: tomar el modelo de la rueda de la bicicleta, trazarlo e inscribir un hexágono regular dentro de su circunferencia.
¿Cuántos triángulos se formaron y de qué tipo dentro del hexágono?
Se formaron seis triángulos equiláteros que conforman el hexágono.
Ahora observa el ángulo que se forma entre dos rayos consecutivos.
¿Cómo se llamará este ángulo?
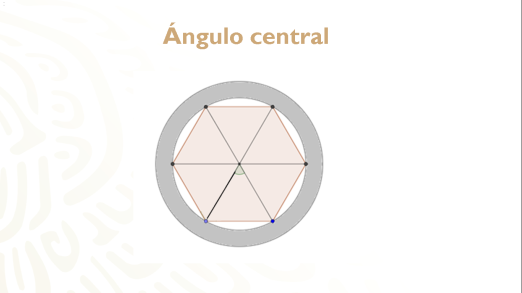
Se llama ángulo central.
Nota que el centro del polígono regular está a la misma distancia de los vértices.
¿Cómo encontramos el centro?
En este caso en que el polígono tiene un número de lados par, el centro del polígono regular coincide con la intersección de algunas de sus diagonales.
¿Cómo determinas el ángulo central?
Primero identificas el ángulo central.
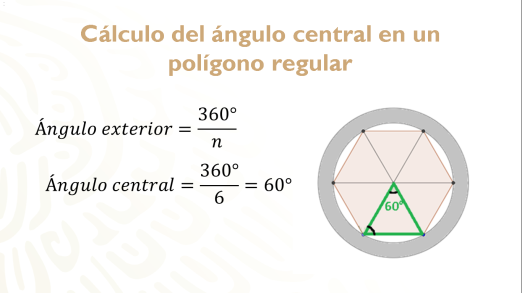
Como puedes apreciar, el ángulo central es igual al ángulo interior de un triángulo equilátero que lo conforma, y si recuerdas su valor, es de 60 grados.
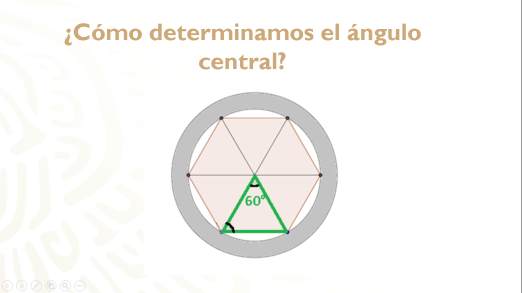
Si analizas que la circunferencia tiene 360° y que será repartida en n lados, entonces el ángulo central lo encontrarás con la fórmula: trescientos sesenta entre ene.
Así que 360° entre 6 es igual a 60 grados.
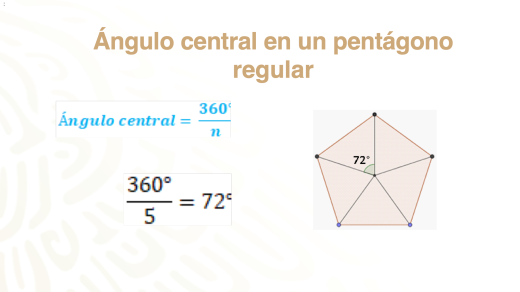
Ahora que sabes cómo determinar el ángulo central, calcula el de un pentágono regular.
¿Cómo lo harás?
Ya sabes que para calcularlo sólo dividirás 360 grados entre 5 y obtendrás 72 grados.
El ángulo central en un pentágono regular es igual a 72°.
¿Te es familiar este ángulo?
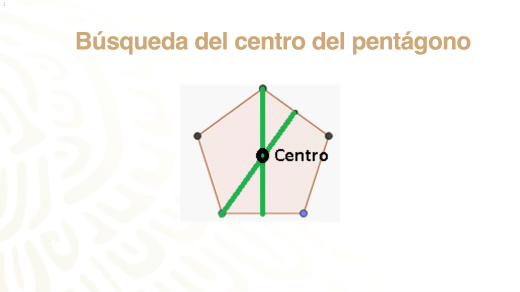
Pero, geometricamente, ¿cómo encuentras el centro del pentágono, si en este caso es un polígono de número de lados impar?
Ya no usarás las diagonales, ahora utilizarás las mediatrices o los segmentos que van del punto medio de un lado del polígono hasta su vértice opuesto, esto mismo se hace sobre los lados para que obtengamos una intersección que corresponderá al centro del polígono regular.
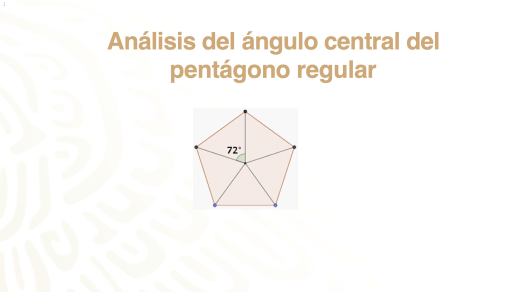
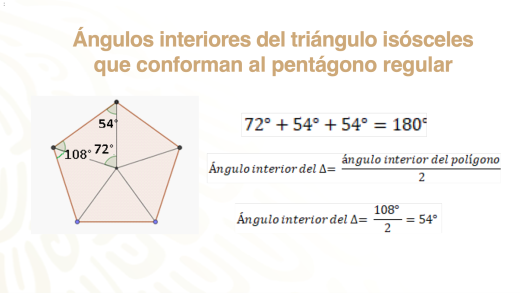
Una vez ubicado el centro, a partir de éste, traza los segmentos que lo unen con los vértices. Observa que se forman 5 triángulos, pero ahora ya no son equiláteros, sino isósceles.
Ya sabes que un ángulo interior del triángulo isósceles, el central, tiene un valor de 60°, ¿qué valor tienen los otros dos ángulos interiores del triángulo isósceles que se formó?
Si la suma de los ángulos en un triángulo es de 180 grados, y ya tienes el valor del ángulo central, los otros dos deben tener un valor de 54 grados porque: 72°+ 54° + 54° = 180°
Entonces, para calcular el ángulo interior adyacente al lado de los triángulos que forman el pentágono, basta con dividir entre dos el ángulo interior del pentágono.
Así, 108 entre 2 es igual a 54 grados.
Recapitulando:
En esta sesión has aprendido qué son los ángulos interior, exterior y central de un polígono regular, también has aprendido a determinarlos o calcularlos.

Ahora establecerás las relaciones que existen entre estos ángulos.
¿Qué relación existe entre los ángulos interior, exterior y central?
Como ya lo has calculado, ahora obsérvalos en un pentágono y en un hexágono regular
Para el pentágono regular:
El ángulo interior es 108°, el exterior es 72° y el central es 72°.
¿Cuáles de ellos son iguales?
El ángulo central es igual al ángulo exterior.
Y el ángulo interior y el ángulo exterior son suplementarios, es decir, suman 180 grados.
Ahora ve al hexágono regular: si su ángulo central es de 60 grados, su ángulo exterior será también de 60 grados y el ángulo interior será de 180° menos 60°, igual a 120°.
Observa si esto se cumple para cualquier polígono regular, analízalo para un triángulo equilátero.
El ángulo central lo obtienes al dividir 360° entre 3, igual a 120°, y su ángulo interior sabes que es de 60°, por lo tanto, el ángulo exterior es de 180° menos 60°, es decir, 120°; con ello corroboras que, en efecto, el ángulo central es igual al ángulo exterior.
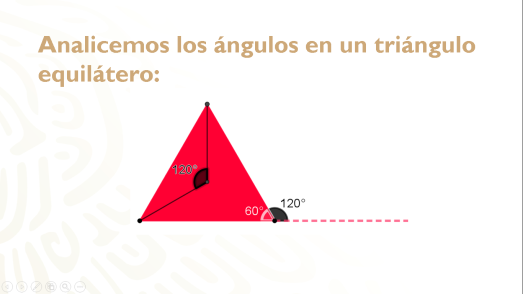

Generalizando las relaciones entre los ángulos de los polígonos regulares, tienes que el ángulo central es igual al ángulo exterior, además, el ángulo interior y el exterior son suplementarios, es decir, suman 180°.
Te has preguntado: ¿para qué nos sirve reconocer la relación entre los ángulos interior, exterior y central en un polígono regular?
El conocer estas relaciones te permite construir e identificar polígonos regulares, mismos que se encuentran en el universo o forman parte de nuestra vida cotidiana; por ejemplo, un panal hexagonal construido por las abejas, la forma pentagonal que tienen las estrellas de mar, los mosaicos hexagonales de adoquín para la construcción, la rueda de la fortuna de forma dodecagonal en una feria o la forma hexagonal que tienen las moléculas de una sustancia química llamada benceno.
El reto de hoy:
Determina el ángulo central en un octágono regular y, a partir de éste, determina su ángulo interior y exterior, y bosqueja el polígono indicando sus ángulos y marcándolos con diferentes colores. Describe con tus palabras los pasos que seguiste para lograr el objetivo.
Ahora reflexiona:
- ¿En qué situaciones se necesitará determinar los ángulos de uno o varios polígonos regulares?
- ¿En qué otras cosas puedes encontrar polígonos regulares?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/






Login to join the discussion