Problemas multiplicativos II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57
Problemas multiplicativos II
Aprendizaje esperado: resolver problemas que impliquen la multiplicación entre una fracción o un decimal y un número natural mediante procedimientos no formales.
Énfasis: resolver problemas que impliquen la multiplicación entre una fracción o un decimal y un número natural mediante procedimientos no formales. (2/2)
¿Qué vamos a aprender?
Aprenderás a resolver problemas que impliquen la multiplicación entre una fracción o un decimal y un número natural mediante procedimientos no formales.
Para explorar más puedes revisar el libro de texto de Desafíos matemáticos de 6º, se explica el tema a partir de la página 19.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/19
¿Qué hacemos?
A continuación, tienes información y algunas actividades que te ayudarán a resolver problemas que impliquen la multiplicación entre una fracción o un decimal y un número natural mediante procedimientos no formales.
En esta sesión resuelve la segunda parte del desafío 8 titulado “El equipo de caminata”. Trabaja con números naturales, fracciones y decimales.
Aplica los conocimientos de las sesiones anteriores, incluida la de ayer: Conceptos básicos de enteros y fracciones.
- Numerador y denominador.
- Fracciones equivalente con decimales: ½=0.5 ¼= 0.25 1/10 = 0.1
- Una vuelta completa al circuito representa nuestra unidad.
- Existen trayectos, conocidos también como circuitos, que inician en el mismo punto y termina una vuelta completa.
Antes de continuar con el ejercicio que estuvimos viendo la clase anterior, debemos integrar un nuevo conocimiento en esta clase.
Vamos a recordar el tema de la división.

Para recuperar lo que realizaste ayer, es momento de leer la consigna del desafío. Lo encuentras en la página 19 del libro de Desafíos Matemáticos, precisamente en el Desafío número 8, se titula “El equipo de caminata”.
Recupera algunos conceptos que aprendiste en la sesión anterior, recuerda los datos o palabras clave que te brinda el texto:
- Equipo de caminata.
- Circuito de 4 km.
- Vueltas.
- Kilómetros recorridos.
Observa ahora la tabla con los datos que obtuviste ayer.

Muy bien, ya recuperaste información importante que te permitirá continuar aprendiendo y resolver la parte pendiente de la tabla, de la primera parte que hiciste anteriormente qué puedes concluir:
- Una vuelta es un entero.
- El entero es de 4 km.
- Entre más vueltas más kilómetros.
- La vuelta se puede partir, dividir o fraccionar en partes iguales.
- Expresar el recorrido en fracciones propias.
- El numerador nos indica cuántas partes del entero recorrió Víctor.
- El denominador nos indica en cuántas partes iguales se divide el entero.
- Podemos usar una división.
Puedes hacer la suma de fracciones, por ejemplo: Cuatro kilómetros entre cuatro es igual a un kilómetro, es decir, un cuarto del circuito equivale a un kilómetro.
4 km entre 4 = 1 km
¼ del circuito equivale a 1 km.
Si la tabla dice que recorrió ¾, entonces: Un cuarto, más un cuatro, más un cuarto, es igual a tres cuartos.

Y como un cuarto es equivalente a un kilómetro del circuito, entonces tendremos que un kilómetro, más un kilómetro, más un kilómetro nos da como resultado, 3 kilómetros.
Actividad 1
Después de recordar estos datos, comienza a resolver la segunda parte del desafío matemático¿qué tan claro quedó el trabajo realizado? Continua con la segunda parte de la tabla.

Según dice, Silvio recorrió 4/5 del circuito. ¿Y qué hiciste para conocer la distancia recorrida? El denominador dice que el entero está dividido en 5 partes, de las cinco partes, ¿Cuántas recorrió Silvio?
Ahora aplica una operación ¿Cuál puede ayudarte a fraccionar 4 km en cinco partes iguales?
Serían 4 kilómetros entre 5, realiza la operación ¿Qué sucede cuando el 5 no cabe en el cuatro? Tienes que emplear el punto decimal correctamente para que el resultado que obtengas sea correcto. Resuelve la división.
El 5 no cabe en el cuatro, en el cociente, arriba del 4 coloca 0.

Junto al 4 coloca el punto decimal y también lo colocas en el cociente, en la misma posición.
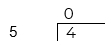
Ahora sí, coloca un cero después del punto que está junto al 4.

Una vez que hiciste lo anteior, sin pensar que tienes un punto entre el 4 y el 0, juntos, ¿Qué número forman? De esa manera, sí puedes pensar en cuántas veces cabe el 5 en el 40, entonces, ¿Qué número multiplicado por 5 te da 40?

Ahora si completas la división: Coloca el 8 arriba y 8X5 = 40 así que en el residuo queda 0.

Por lo tanto, 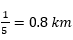 pero Silvio recorrió 4/5.
pero Silvio recorrió 4/5.

Continua, el recorrido de Eric es como puedes observar, se trata de una fracción mixta, pues tienes enteros y partes del siguiente entero.
¿Cómo puedes saber cuántos km recorrió Eric? Puedes trabajar primero los enteros y luego la fracción.
Muy bien, entonces, si recorrió dos vueltas completas, son 2 enteros y ya sabes que cada vuelta es de 4 km, así que 2 vueltas son 8 km. Ya encontraste una parte de la respuesta.
Ahora, ¿Cómo le haces? Aplica lo que realizaste con algunos de los ejercicios anteriores. La fracción es 7/ 8.
Así que tienes que dividir el entero, 4km, en 8 partes iguales, como indica el denominador. Realiza una división utilizando el punto decimal

Por lo tanto, tienes que un octavo es igual a medio kilómetro, es decir, punto cinco.

Así que en 7/8 lo puedes visualizar de esta forma: es decir que 7/8 = a 3.5 km.

Recuerda que Eric recorrió ya habias calculado que 2 enteros eran 8 km, a eso le sumes los 3.5 km de los 7/8 por lo tanto, Eric recorrió 11.5 km.

Continua con el recorrido de Irma, el cual indica que caminó 0.75 del circuito, tu ya sabes que los números decimales también pueden expresarse como fracciones.

La información que acabas de recordar te puede ayudar a encontrar los km del recorrido de Irma.
El siguiente ejemplo: 0.75 es lo mismo que ¾, sólo que uno es un número decimal y el otro es una fracción. Si divides 4 km entre 4 partes, ¼= 1 km, y tomas 3, que es lo que indica el numerador, obtienes 3 km, el recorrido de Irma de 0.75= ¾= 3 km.

Ahora observa el recorrido de Adriana 1.25 vueltas ¿Cómo lo resolverías? el 1 representa 1 entero= 4 km.
En el ejercicio anterior ya identificaste que 0.25= ¼=1 km, así que suma 4 km del entero y 1 km del 0.25 y te da como resultado 5 km por lo tanto, el recorrido de Adriana es de 5 km. El recorrido de Luis es de 1.3 vueltas ¿Ya identificaste por qué? Tienes 1 entero=4 km y 0.3=3/10 cada vez el proceso es más fácil, porque has avanzado poco a poco, así llegas a problemas más complicados, pero como estás muy atento a la sesión, se va haciendo menos difícil.
Tienes que dividir 4 km en 10 partes iguales porque necesitas 3/10.

Por lo tanto, el resultado del recorrido de Luis, de 1.3 vueltas, es igual a 5.2 km. ¡Ya sólo falta uno!
Así que no te desespes, este no es un tema sencillo y necesitas de toda tu atención.

El recorrido de María es de 2.6 vueltas del circuito, es un ejercicio que requiere hacer lo mismo que el anterior, intenta hacerlo solo, para que comparemos resultados. mientras tú lo haces voy llenando los resultados que hoy trabajaste.
Si el recorrido de María es de 2.6 vueltas. 2 vueltas = 8 km. Como 0.6 = 6/10. En el problema anterior vimos que 1/10 representa 0.4 km.

2.6 vueltas = 8 km + 2.4 km = 10.4 km, entonces María recorrió 10.4 km

¿Obtuviste el mismo resultado? muy buen trabajo. Anota los resultados para que realices la autoevaluación en casa, si no te salieron iguales, no te preocupes, sigue practicando este tema muy de cerca.

El reto de hoy:
Revisar el tema en el portal de Aprende en casa II por cualquier cosa que no hayas entendido.
Si en tu casa hay libros relacionados con el tema, consúltalos, así podrás saber más, si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion