Propiedades de los polígonos irregulares

Propiedades de los polígonos irregulares

Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.

Énfasis: desarrollar el razonamiento deductivo al examinar las propiedades de los polígonos irregulares.

¿Qué vamos a aprender?

Continuarás con el estudio de problemas que implican obtener el número de diagonales que pueden trazarse desde un vértice, el número de diagonales en total y la suma de los ángulos interiores. En esta sesión, te enfocarás en los polígonos “irregulares”.

¿Qué hacemos?

Retoma el problema de la casa de Alma que se abordó la sesión pasada. Ahora, analizarás los polígonos irregulares.

Problema 1

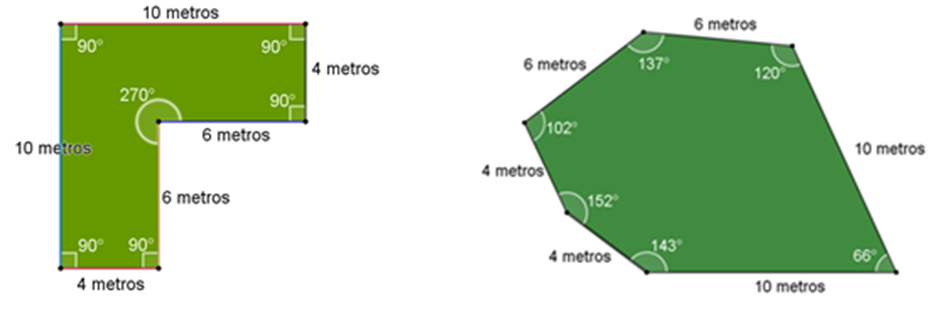
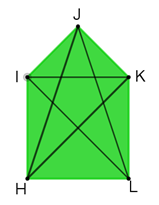
Alma tiene una casa en el interior de un terreno, como se muestra en la siguiente figura:

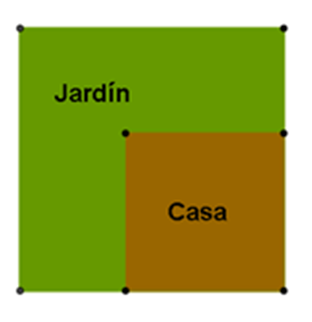
¿Qué forma tienen la casa y el jardín?

La casa está construida sobre un terreno cuadrado, y el área restante que le corresponde al jardín es un hexágono porque tiene seis lados.

En la sesión pasada identificaste que el área de la casa es un cuadrado, el cual es un polígono regular, sin embargo, la forma que tiene el jardín no lo es.

Reflexiona en lo siguiente:

¿Cómo puedes diferenciar los polígonos regulares de los irregulares?

Los polígonos regulares se diferencias de los irregulares porque en los polígonos regulares la amplitud de todos sus ángulos interiores es la misma, es decir, son congruentes, y también todos sus lados tienen la misma longitud, a diferencia de los irregulares donde no se cumple una de estas condiciones.

Ahora, analiza los lados y los ángulos del terreno del jardín.

Cuenta con seis lados, con ello sabes que se trata de un hexágono, pero ¿a qué tipo de hexágono corresponde la forma que tiene el jardín?

Para contestar esta pregunta, debes examinar cómo son sus lados y sus ángulos.

Primero examina: ¿cuál es la longitud de cada uno de los lados del terreno en el cual se encuentra el jardín?

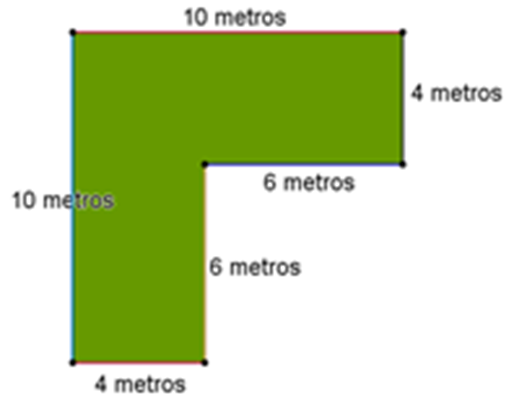
Las longitudes de sus lados son de 4, 6, 6, 4, 10 y 10 metros, es decir, dos de sus lados miden 4 metros, otros dos miden 6 metros y los otros dos miden 10 metros.

Esto indica que la forma que tiene el terreno de Alma corresponde al de un hexágono irregular, ya que sus lados no tienen la misma longitud.

Ya que conoces la longitud, analiza los ángulos interiores en el hexágono.

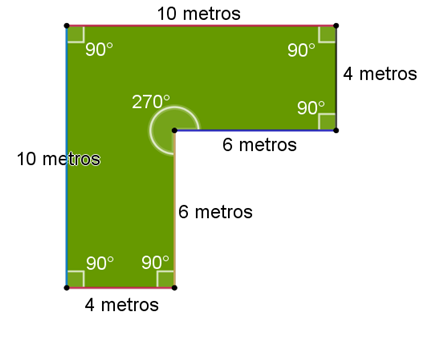
Se puede identificar que cinco ángulos miden 90 grados, y otro ángulo mide 270 grados.

Con esto se corrobora que este hexágono no es un polígono regular, porque sus lados no tienen la misma longitud y sus ángulos interiores tampoco tienen la misma amplitud.

Reflexiona:

¿Se puede trazar un hexágono irregular con las mismas medidas de los lados que tiene el jardín de Alma, pero que cada uno de los ángulos interiores mida menos de 180º?

Ahora, realiza lo siguiente:

Comprueba lo anterior y traza en tu cuaderno un hexágono irregular en el que las longitudes de 10, 10, 6, 6, 4 y 4 metros sean contiguas, es decir, que aparezcan una seguida de la otra, de tal forma que todos los ángulos interiores sean menores de 180 grados.

Seguramente trazaste diferentes hexágonos irregulares, sin embargo, aunque su forma es parecida a la de un hexágono regular, no lo es, ya que las longitudes de sus lados no son iguales.

Probablemente dibujaste un hexágono similar al siguiente:

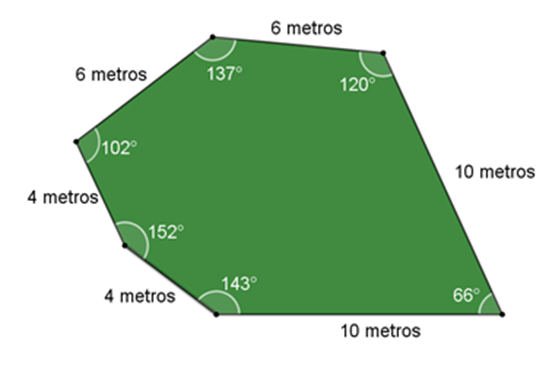
Los ángulos interiores no son iguales, pero todos ellos miden menos a 180º. Sus ángulos miden 66, 120, 137, 102, 152 y 143 grados.

Ahora compara los hexágonos con los que has trabajado hasta este momento.

¿Cuáles son las semejanzas y las diferencias entre los hexágonos anteriores?

Primero, ambos polígonos tienen seis lados, por lo tanto, son hexágonos.

Segundo, en ambos polígonos las longitudes de sus lados son diferentes, por ello, son hexágonos irregulares.

Tercero, uno de los ángulos del primer hexágono es mayor de 180 grados, mientras que todos los ángulos en el segundo hexágono son menores a 180 grados.

¿Cuál de ellos se parece a una figura circular o redondeada?

El polígono que se parece más a una figura redondeada es el de la derecha, esto sucede cuando sus ángulos interiores miden menos de 180 grados; a este tipo de figuras se les llama polígonos convexos.

Y a los polígonos que tienen uno o más ángulos interiores mayores de 180 grados se les denomina cóncavos, como la forma que tiene el jardín de Alma.

De acuerdo con esta clasificación, realiza lo siguiente:

Reflexiona si puede haber polígonos regulares cóncavos o polígonos regulares convexos, y anota en tu cuaderno los argumentos mediante los cuales puedes determinarlo.

Recapitula.

Para determinar que un polígono es irregular, basta con saber que no todos sus lados tienen la misma longitud, o que no todos sus ángulos interiores tienen la misma amplitud.

Los polígonos se pueden clasificar, de acuerdo con sus ángulos interiores, como convexos o cóncavos.

Los polígonos convexos son aquellos que tienen sus ángulos interiores menores a 180 grados, mientras que los cóncavos tienen uno o más ángulos interiores mayores a 180 grados.

A continuación, a través del siguiente problema, analiza las diagonales que pueden trazarse desde un vértice y las diagonales totales de los polígonos irregulares.

Problema 2

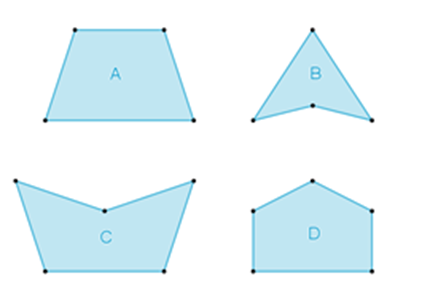
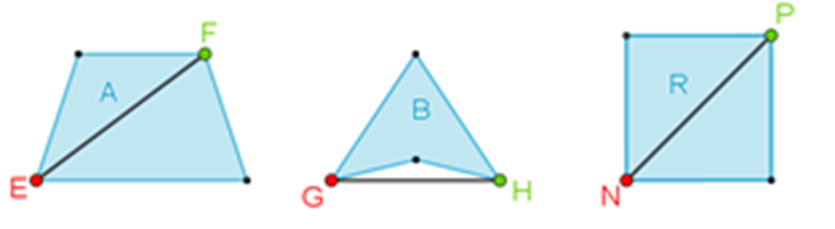
En un balneario se tienen cuatro diferentes diseños de albercas, como se muestra en la siguiente figura:

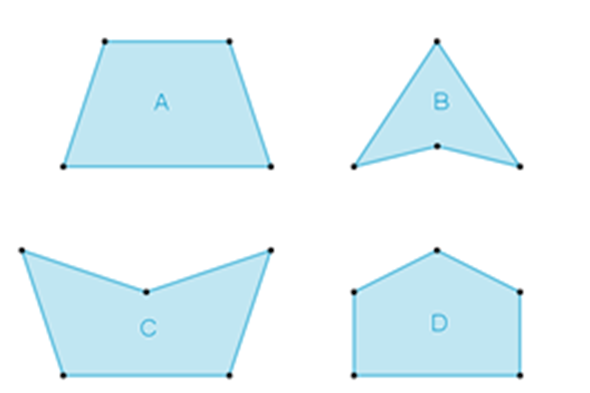
Los estudiantes que asisten al balneario quieren seleccionar las albercas en las que puedan nadar de un vértice a otro vértice no consecutivo sobre sus diagonales, partiendo de cualquiera de los vértices.

Recuerda que las diagonales son segmentos de recta que se pueden trazar desde un vértice hacia otro vértice no consecutivo. De acuerdo con esta especificación, ¿cuáles albercas elegirías?, ¿por qué?

Para resolver este problema, es necesario que analices a detalle la forma que cada una de las albercas tiene, e identifiques en las que sí se podría nadar de un vértice a cualquier otro vértice no consecutivo a través de sus diagonales, partiendo de cualquiera de sus vértices.

Examina cada una de las albercas.

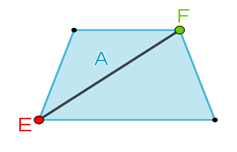
En la alberca “A”.

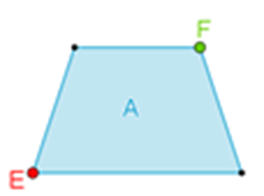
Se identifica que tiene 4 lados, dos de ellos son paralelos y los otros dos no lo son, entonces se trata de una alberca con forma de trapecio.

Todos los ángulos interiores del trapecio son menores de 180 grados, por ello, se puede decir que el polígono es convexo. Además, si te colocas en cualquiera de sus vértices, puedes nadar hacia el vértice no contiguo, es decir, a través de sus diagonales.

Marca la diagonal que se puede trazar desde el vértice “E” hasta el vértice “F”.

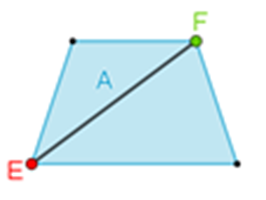
¿Es posible nadar desde el punto “E” hasta el “F” por medio de su diagonal?

Se reconoce que sí se puede nadar desde “E” hasta “F” por medio de su diagonal. Y si te colocas en cualquiera de los vértices, puedes darte cuenta de que sí puedes nadar por medio de sus diagonales.

Alberca “B”.

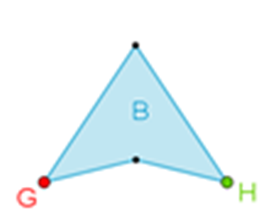
La alberca “B” tiene cuatro lados, entonces es un cuadrilátero; además, tiene dos lados con la misma longitud y los otros dos lados con otra misma longitud, pero no tiene lados paralelos.

Uno de sus ángulos interiores es mayor de 180 grados, esto quiere decir que la alberca tiene forma de un polígono cóncavo.

Marca la diagonal que se puede trazar desde el vértice “G” hasta el vértice “H”.

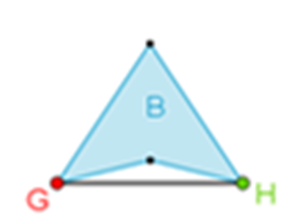
¿Es posible nadar desde el punto “G” hasta el “H” por su diagonal?

No se puede nadar desde “G” hasta “H”, podrías caminar por fuera de la alberca, pero no es posible nadar.

Reflexiona: ¿por qué no es posible nadar desde el punto “G” hasta el “H”?

No es posible nadar desde “G” hasta “H” porque esta diagonal se encuentra en el exterior de la alberca, es decir, en el exterior del polígono, pero podrías nadar por otra de sus diagonales.

Alberca “C”.

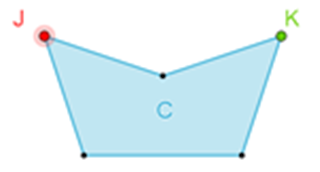
La alberca “C” tiene cinco lados, entonces su forma es pentagonal; además, tiene dos pares de lados de la misma longitud y otro de sus lados tiene mayor longitud, por lo tanto, el pentágono es irregular.

Se advierte que uno de sus ángulos interiores es mayor de 180 grados, por lo cual se puede decir que es un pentágono irregular cóncavo.

Marca la diagonal que se puede trazar desde el vértice “J” hasta el vértice “K”.

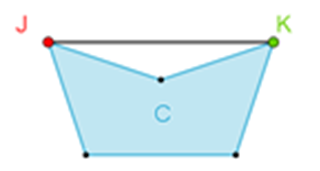
¿Es posible nadar por medio de esa diagonal?

No se puede nadar por medio de esa diagonal porque ésta se encuentra en el exterior de la alberca; sin embargo, hay otras dos diagonales que sí permiten nadar siguiendo su trayectoria.

Alberca “D”.

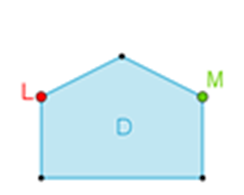
Esta alberca tiene forma de un pentágono irregular, tiene dos lados paralelos y todos sus ángulos interiores son menores a 180 grados, entonces se trata de un pentágono irregular convexo.

Ahora marca la diagonal que se puede trazar desde “L” hasta “M”.

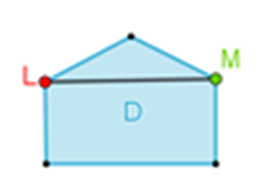
Imagina todas las diagonales que se pueden trazar desde todos los vértices. Todas sus diagonales que se encuentran en el interior de la alberca, por lo tanto, sí se puede nadar a través de sus diagonales.

Has analizado los cuatro diseños de las albercas, y se destaca de que en los diseños “A” y “D” sí se puede nadar siguiendo la trayectoria de sus diagonales partiendo desde cualquiera de los vértices, porque sus diagonales se encuentran en el interior de ellas. Pero en los diseños “B” y “C” una de sus diagonales se encuentra en el exterior, y es por ello que no se podría nadar siguiendo la trayectoria de esas diagonales.

Reflexiona acerca de esta situación:

¿Qué forma debe tener la alberca para que sea posible nadar de vértice a vértice por medio de las diagonales partiendo desde cualquiera de sus vértices? Es decir, ¿qué tipo de polígono permite nadar a través de cualquiera de sus diagonales?

En los diseños “A” y “D”, las albercas tienen forma de polígonos irregulares convexos y sí es posible nadar siguiendo la trayectoria de sus diagonales partiendo desde cualquiera de sus vértices.

En los diseños “B” y “C”, las albercas tienen forma de polígonos irregulares cóncavos y no en todos los casos es posible nadar siguiendo la trayectoria de sus diagonales partiendo desde cualquiera de sus vértices. Cabe aclarar que, aunque algunas de sus diagonales se encuentran en el interior de las albercas, por lo menos una de ellas se encuentra en el exterior.

Entonces, ¿a qué se debe que las diagonales se encuentren en el interior o en el exterior de la alberca?, ¿qué tipo de polígonos deben ser?

Para que las diagonales se encuentren en el interior de la alberca o de cualquier polígono, éstos deben ser convexos.

Has aprendido a identificar los polígonos irregulares, a clasificarlos de acuerdo con los ángulos en convexos o cóncavos, y a determinar, con base en esto, si las diagonales se encuentran en el interior o en el exterior del polígono.

Para saber cómo obtener el número de diagonales que se pueden trazar desde un vértice, y el número de diagonales totales que se pueden trazar en un polígono irregular, analiza el siguiente problema.

Problema 3

Considerando el diseño de las cuatro albercas, ¿cuántas diagonales se pueden trazar desde un vértice?

En el diseño “A”, se puede trazar una sola diagonal si se coloca en el vértice “E”.

Para el diseño “B”, que también es un cuadrilátero, se puede trazar una sola diagonal si se coloca en el vértice G.

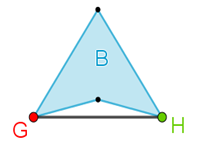
¿Qué sucede si se comparan las diagonales que se pueden trazar desde un vértice con las de un polígono regular? Es decir, ¿cuál será el número de diagonales que tiene un cuadrado?

Para un cuadrado, el número de diagonales que se pueden trazar desde un vértice sólo es una. De lo anterior, se puede concluir que para cualquier tipo de cuadrilátero sólo es posible trazar una diagonal desde un vértice. 

¿Sucede lo mismo en los pentágonos?

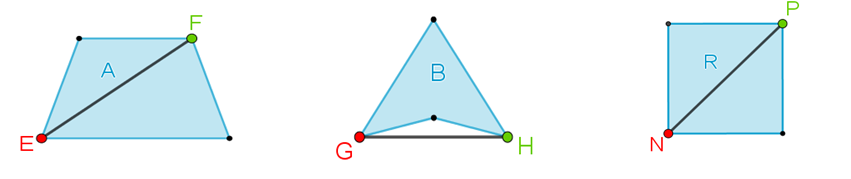
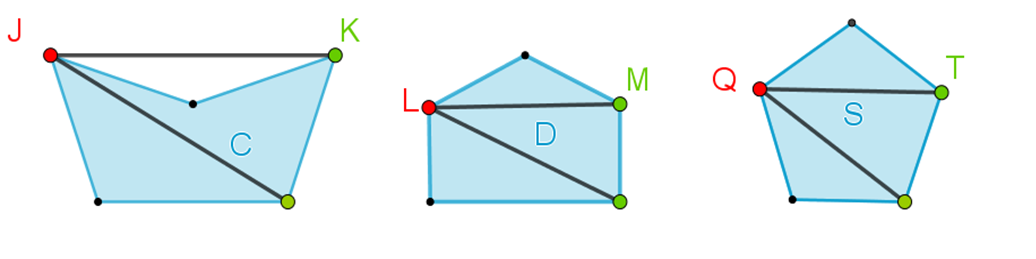
Analiza las albercas “C” y “D”, y agrega la alberca pentagonal regular “S”.

¿Cuántas diagonales se pueden trazar desde los vértices J, L y Q para las albercas C, D y S, respectivamente?

Desde los puntos “J”, “L” y “Q” se pueden trazar sólo dos diagonales para cada pentágono, sean o no polígonos cóncavos o convexos, irregulares o regulares.

¿Se puede predecir cuántas diagonales se podrían trazar desde un vértice para un hexágono sin marcarlas en el polígono?

Para un cuadrilátero se puede trazar una diagonal desde un vértice, y para un pentágono se pueden trazar dos, entonces para un hexágono serán tres y así sucesivamente.

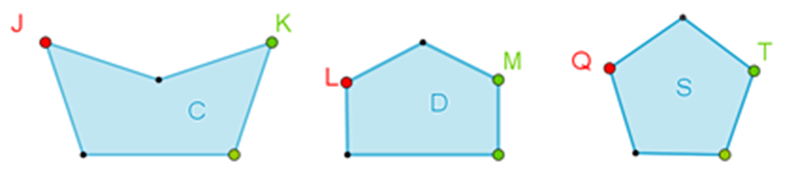
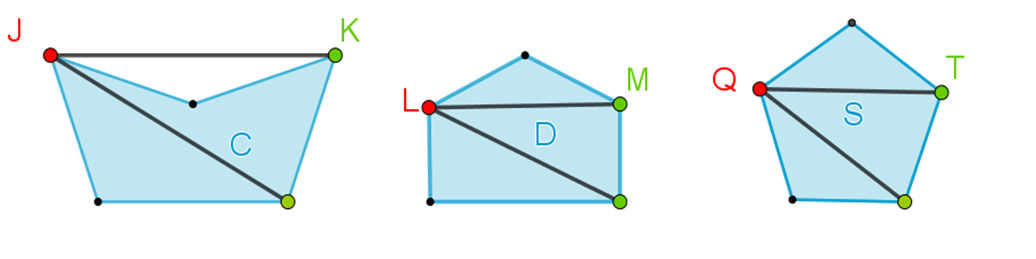
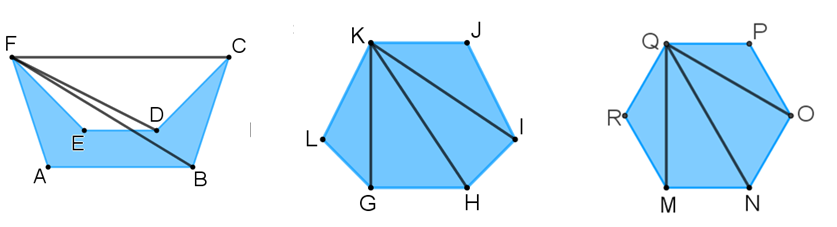
Corrobora que por cada vértice en un hexágono se pueden trazar tres diagonales. Examina los siguientes tres hexágonos:

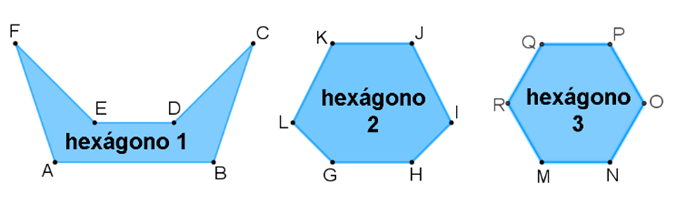
Ahora, elige un vértice para cada uno de los hexágonos.

Selecciona el vértice F para el hexágono 1:

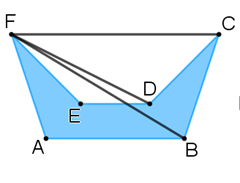
Se comprueba en este hexágono irregular cóncavo que tiene tres diagonales desde un vértice.

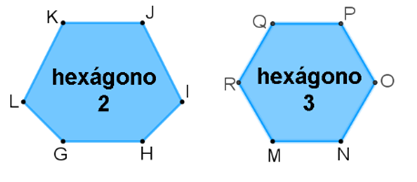
Continúa con los otros dos hexágonos convexos, 2 y 3:

Marca las diagonales que se pueden trazar desde los vértices “K” y “Q” en ambos hexágonos.

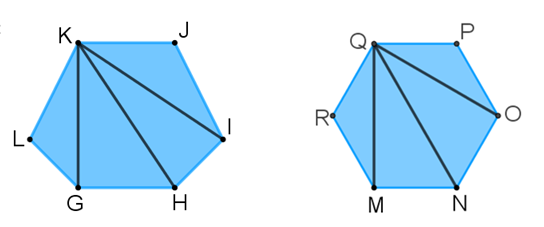
Para un hexágono regular o irregular, cóncavo o convexo, son tres el número de diagonales que se pueden trazar desde un vértice.

Ahora, consigue una generalización que te permita calcular el número de diagonales que pueden trazarse desde un vértice para un polígono irregular.

Recuerda que, para un polígono regular de “n” lados, el número de diagonales que se pueden trazar desde un vértice es:

n - 3

Reflexiona:

¿Cumple esta generalización para cualquier tipo polígono?

Para cualquier cuadrilátero, por un vértice, se puede trazar una sola diagonal. Ahora obtén el número de diagonales usando la generalización n-3.

En un cuadrilátero, n = 4, al sustituirlo en n-3, se obtiene:

Número de diagonales que se pueden trazar

desde un vértice = n - 3 = 4 – 3 = 1

¿Consideras que n-3 es una expresión general válida para obtener el número de diagonales que se pueden trazar desde un vértice en cualquier polígono regular o irregular, cóncavo o convexo?

Confirma si esto se cumple para los pentágonos y para los hexágonos que has analizado anteriormente.

En los pentágonos el número de diagonales que se pueden trazar desde un vértice son dos.

En un pentágono, n = 5, al sustituirlo en la generalización n - 3, se tiene:

Número de diagonales que se pueden trazar

desde un vértice = n - 3 = 5 – 3 = 2

Por lo tanto, es el mismo número de diagonales que se obtuvo al realizar el análisis.

Para los hexágonos, el número de diagonales que se pueden trazar desde un vértice son tres.

En un hexágono, n = 6, al sustituirlo en la generalización n - 3, se tiene:

Número de diagonales que se pueden trazar

desde un vértice = n - 3 = 6 – 3 = 3

Por lo tanto, con la expresión algebraica “n – 3”, puedes obtener el número de diagonales que pueden trazarse desde un vértice para cualquier tipo de polígono, sea regular o irregular, cóncavo o convexo.

Reflexiona en lo siguiente:

¿Por qué a “n” hay que restarle tres?

Analiza esta situación con el hexágono 2.

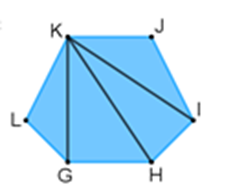
Teniendo en cuenta que la diagonal es un segmento de recta que une dos vértices no consecutivos en un polígono, los segmentos de recta que unen al vértice “K” con los dos vértices contiguos “J” y “L” no son diagonales, sólo son dos de los lados del polígono, por esta razón no se pueden considerar los vértices “J” y “L”.

Ahora, ¿has pensado cómo puedes obtener una expresión que te permita calcular el número de diagonales totales para cualquier polígono regular o irregular, convexo o cóncavo?

Analiza cuántas diagonales se pueden trazar en total en los polígonos irregulares. Para ello, recurre a examinar los primeros polígonos.

¿Cuántas diagonales tiene un triángulo?

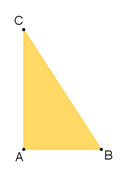
Un triángulo no tiene diagonales, ya que, si se toma como referencia el vértice “A”, los vértices “B” y “C” son contiguos, y para que fueran diagonales, tendrían que ser vértices consecutivos.

¿Cuántas diagonales en total tiene un cuadrilátero?

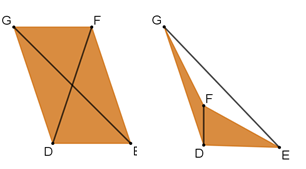
Tanto el cuadrilátero convexo como el cóncavo cuentan con dos diagonales.

¿Cuántos vértices en total tiene un pentágono?

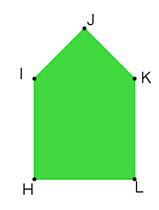
El pentágono cuenta con 5 vértices, el “H”, el “I”, el “J”, el “K” y el “L”.

¿Cuántas diagonales se pueden trazar por cada vértice?

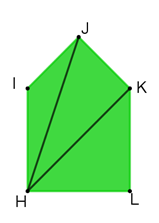
Se pueden trazar dos diagonales por cada vértice. Si usas la expresión “n - 3”, y como “n” es igual a 5, ya que corresponde al número de lados del polígono, entonces se tiene 5 – 3 = 2.

Si tienes dos diagonales por cada vértice y tienes cinco vértices, ¿cuántas diagonales tendrías en total?

Son cinco, pero si se multiplica el número de vértices, 5, por el número de diagonales que se pueden trazar desde un vértice, que son dos, parece que son diez diagonales en total y no cinco.

¿Por qué sucede esto?

Porque al multiplicar 5 por dos, que es “n”, por n - 3, se están considerando dos veces cada una de las diagonales. Por ejemplo, la diagonal “L-J” y la diagonal “J-L” es la misma, y la se está contabilizando dos veces.

Para que esto no suceda, ¿qué se debe de hacer?

Dividir entre dos, es decir:

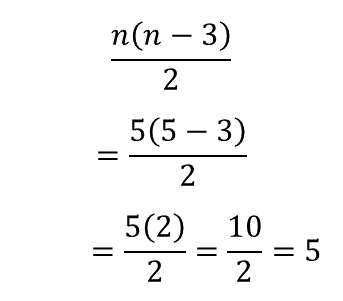
De acuerdo con la expresión anterior, ¿cuántas diagonales totales tiene un hexágono irregular?

Un hexágono tiene seis lados, entonces “n” es igual a 6, al sustituirlo en la expresión:

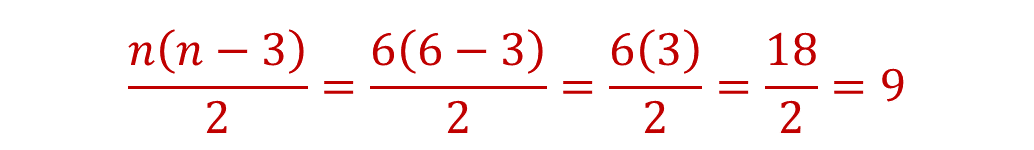
Son nueve todas las diagonales que se pueden trazar en un hexágono irregular.

Observa las siguientes figuras y compruébalo:

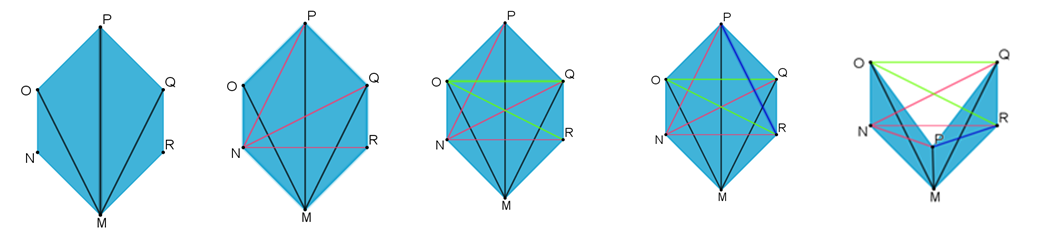
En total son nueve.

Como puedes observar, el número de diagonales que se pueden trazar en un polígono no se modifica si éste es convexo o cóncavo.

En conclusión, para determinar el número de diagonales totales que se pueden trazar en cualquier tipo de polígono, se puede usar la expresión:

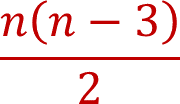
Has aprendido a generalizar por medio de una expresión el número de diagonales que se pueden trazar desde un vértice para cualquier tipo de polígono. También obtuviste una expresión que te permite calcular el número de diagonales totales que se pueden trazar en cualquier tipo de polígono.

Finalmente, para obtener la suma de los ángulos interiores de cualquier tipo de polígono, analiza los siguientes polígonos irregulares:

Comienza con el triángulo:

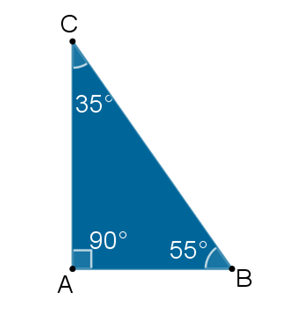
En este triángulo, cada uno de sus ángulos interiores mide 90, 55 y 35 grados. ¿Cuánto mide la suma de sus ángulos interiores?

La suma de los ángulos interiores de este triángulo es:

90° + 55° + 35° = 180°

La suma de los ángulos interiores en un triángulo equilátero es de 180 grados; asimismo, sin importar si el triángulo es regular o irregular, la suma de sus ángulos interiores será de 180°.

Continúa con el pentágono:

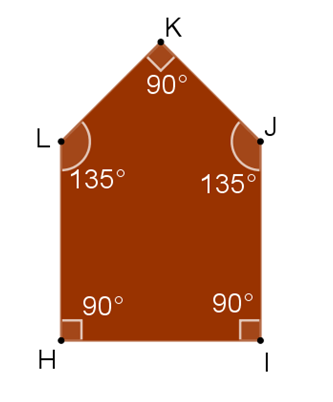
Este polígono irregular tiene cinco ángulos interiores, tres de ellos miden 90 grados y los otros dos restantes miden 135 grados. Por lo tanto, la suma de los ángulos interiores se obtiene de la siguiente manera:

3 (90°) + 2 (135°) = 270° + 270° = 540 °

La suma de los ángulos interiores en un pentágono regular también es de 540 grados. Entonces, sin importar si el pentágono es regular o irregular, la suma de sus ángulos interiores será de 540°.

Por lo tanto, la suma de los ángulos interiores para los polígonos irregulares es igual a la de sus polígonos regulares correspondientes.

¿De qué depende la suma de los ángulos interiores de cualquier polígono?

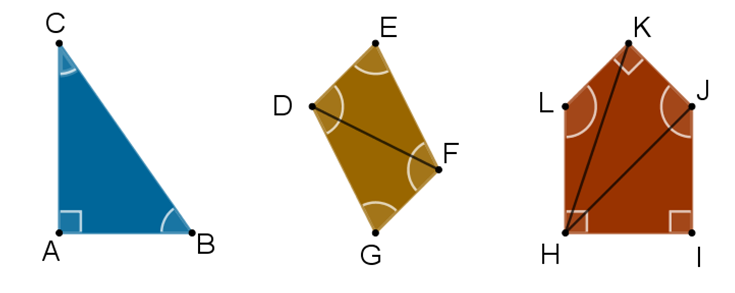
Depende del número de triángulos en los que puede dividirse el polígono mediante las diagonales que pueden trazarse desde uno de sus vértices.

En resumen, para un polígono irregular también se cumple que:

• El número de diagonales que se pueden trazar desde un vértice es:
  n – 3
• El número de diagonales totales es:
  
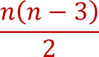
• Y la suma de los ángulos interiores de un polígono es de:

180 grados (n – 2)

El reto de hoy:

Elabora tus notas considerando las ideas más importantes del tema de esta sesión.

Consulta tu libro de texto de matemáticas y resuelve los ejercicios referentes a los polígonos irregulares.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/