El método más pertinente

El método más pertinente

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas y verificar que el resultado es la respuesta de la situación planteada.

¿Qué vamos a aprender?

Analizarás diferentes problemas que se representan matemáticamente utilizando sistemas de dos ecuaciones con dos incógnitas, así mismo estudiarás la utilidad de los diversos métodos para su resolución y conocerás la importancia de comprobar que el resultado cumpla con las condiciones establecidas en el planteamiento inicial del problema.

Encontrar la solución de un sistema de ecuaciones 2x2, significa obtener los valores de las dos incógnitas, es decir, los valores que hacen verdaderas simultáneamente, ambas ecuaciones.

Para la resolución de problemas-situaciones a través de un sistema de ecuaciones 2x2, lo importante es comprender los procedimientos, y pensar en cómo usar las relaciones y las propiedades de los números y las operaciones para su resolución.

Asimismo, hay técnicas que te pueden ayudar a resolver los sistemas de dos ecuaciones lineales con dos incógnitas, como la técnica del ensayo y refinamiento, o el registro tabular. Todos estos recursos, métodos y estrategias ayudan y mejoran tu capacidad para resolver y plantear problemas matemáticos.

En esta clase identificarás, de los métodos de resolución que se han visto hasta este momento, cuál es el método más adecuado para resolver una situación-problema que requiere representarse a través de un sistema de dos ecuaciones con dos incógnitas:

• Método gráfico.
• Método de igualación.
• Método de sustitución.
• Método de suma y resta o de eliminación.

¿Qué hacemos?

Analiza la siguiente situación-problema y resuelve a través de un sistema de dos ecuaciones con dos incógnitas utilizando el método más conveniente.

Situación-problema 1

Un terreno rectangular tiene un perímetro de 380 metros y mide 50 metros más de largo que de ancho.

¿Cuáles son las dimensiones del terreno?

1. ¿Cuáles son las incógnitas?
   “x" y “y”, donde “x” representa la medida del largo del terreno, y “y” la medida de su ancho.
2. ¿Qué sistema de ecuaciones representa la situación?
   
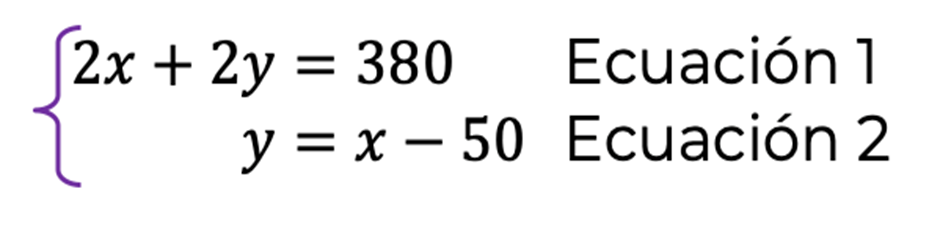
   Ecuación 1. Lo cual significa que, si al sumar dos veces la medida de lo largo, más dos veces la medida de lo ancho, se obtiene el perímetro del rectángulo.
   Ecuación 2. Lo cual significa que, si a la medida de lo largo se le restan 50, se obtiene la medida de lo ancho.
3. ¿Qué características tiene el sistema de ecuaciones? Sin resolverlo, ¿qué método te parece más eficiente de usar?

Método de sustitución.

¿Por qué?

En este caso, ya está despejada la incógnita “y” y se puede sustituir en la ecuación 1. 

Usarás los métodos de sustitución, igualación, de suma y resta, y finalmente, el gráfico. Esto con la finalidad de comprobar si el método de sustitución era el adecuado.

Método de Sustitución

Como ya se tiene despejada la incógnita “y” en la segunda ecuación. Se procede a sustituir el valor algebraico de “y” en la ecuación 1:

Para despejar la incógnita “x”, se utilizaron las propiedades de los números y las operaciones, entonces se canceló “cien” en el primer miembro de la igualdad al sumar 100, en ambos miembros de la ecuación. Por lo que se obtuvo el resultado, x=120.

Se sustituye x=120 en la ecuación 2:

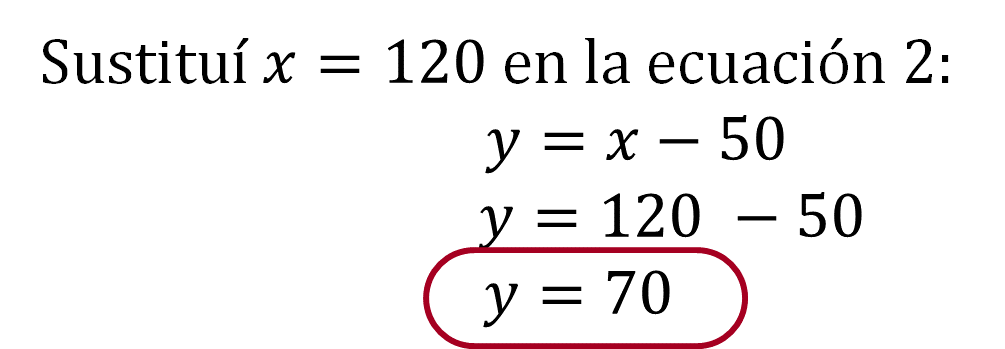
Después de haber obtenido el resultado de la incógnita “y”, se comprueba en la ecuación 1:

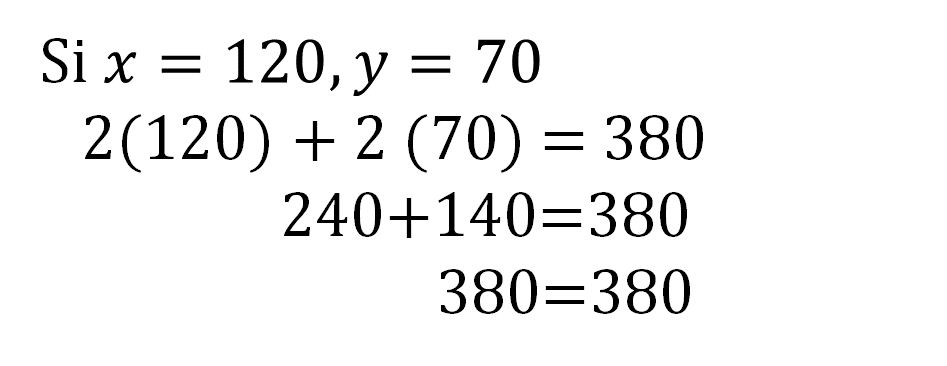
Por lo tanto, las medidas del largo y ancho del terreno rectangular que tiene un perímetro de 380 son 120 m y 70 m; al comparar ambos números, se sabe que el largo mide 50 metros más que el ancho. Se obtuvo la solución del sistema de dos ecuaciones con dos incógnitas, mediante el método de sustitución.

Método de Igualación

Para resolver el mismo sistema, ahora con el método de igualación, se tiene que despejar la misma incógnita en ambas ecuaciones e igualar las expresiones que resulten.

Se puede suponer que ambas valen lo mismo; esa es la base para afirmar que pueden ser igualadas. Al igualar las expresiones se forma una ecuación con una incógnita, la cual se resolverá al hacer los despejes necesarios.

Una vez obtenido el resultado, se despeja en alguna ecuación original para calcular el valor de la otra incógnita.

Sistema de ecuaciones:

Se despeja la incógnita “y”, en la ecuación 1:

Se usaron las propiedades de los números y las operaciones para cancelar (2x) en el primer miembro de la igualdad al sumar su inverso aditivo, que es (-2x), en ambos miembros de la ecuación. Por lo tanto, se obtiene el despeje de la incógnita “y”, en la ecuación 1.

Como ya se cuenta con el despeje de “y” de la ecuación 2 desde el inicio, se procede a igualar el despeje de “y” en ambas ecuaciones, 2 y 1:

Se suma el inverso aditivo de (-x) que es (x), para obtener el resultado de la incógnita:

Después, se sustituye “x” en la ecuación 2 para obtener el valor de “y”:

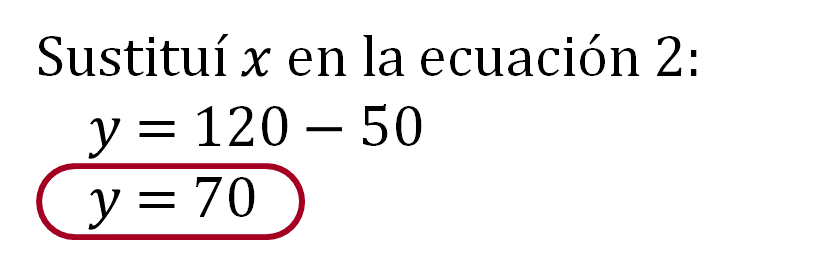
Finalmente, se comprueba en la ecuación 2:

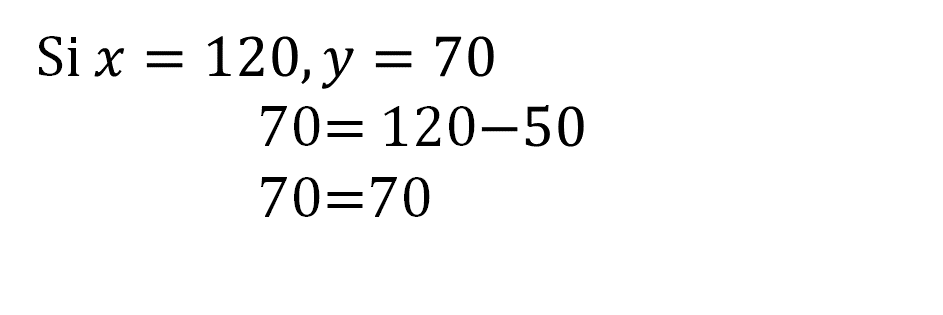
Con ambos métodos se obtiene la misma solución al sistema de dos ecuaciones con dos incógnitas. La diferencia radica en la manera en cómo se razona para su resolución, y en la aplicación de las propiedades de los números y las operaciones.

Método de Suma y Resta

El método de suma y resta consiste en operar con las dos ecuaciones del sistema, la finalidad es eliminar algunos de los términos, es decir, reducir términos semejantes, con la intención de encontrar una ecuación lineal con una incógnita. Para ello se deben hacer simétricos los coeficientes de la incógnita que se quiere reducir.

Primero se ordenan términos semejantes, en la ecuación 2. Para igualar los coeficientes de las ecuaciones, se multiplica la ecuación 2 por dos, para que las incógnitas sean iguales a la ecuación 1.

Se establece la suma. Y se realiza la operación en las dos ecuaciones.

Por lo tanto, se obtiene el valor de “y”, igual a 70.

Ahora, se sustituye “y” en la ecuación 2 del sistema.

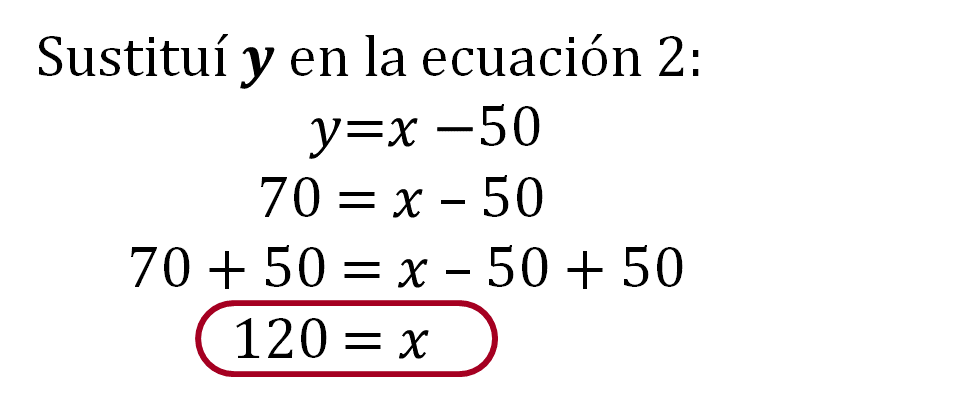
Finalmente, se utilizan los valores de x=120 y de y=70, y se comprueba utilizando la ecuación 1.

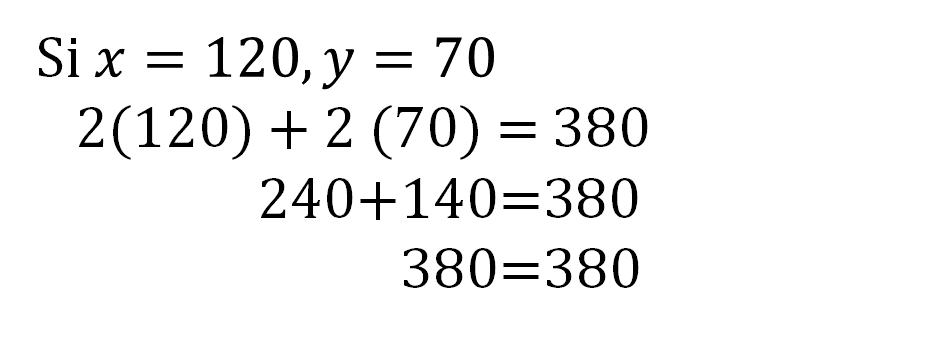
Método Gráfico

Es un procedimiento de resolución que consiste en representar las gráficas asociadas con cada ecuación del sistema.

Para realizarlo, es necesario tabular las ecuaciones, despejando en particular la incógnita (y) y asignando posibles valores a la otra incógnita (x) y así, obtener pares ordenados que representan las coordenadas en el plano cartesiano. La coordenada (x, y) del punto donde coinciden las gráficas es la solución del sistema.

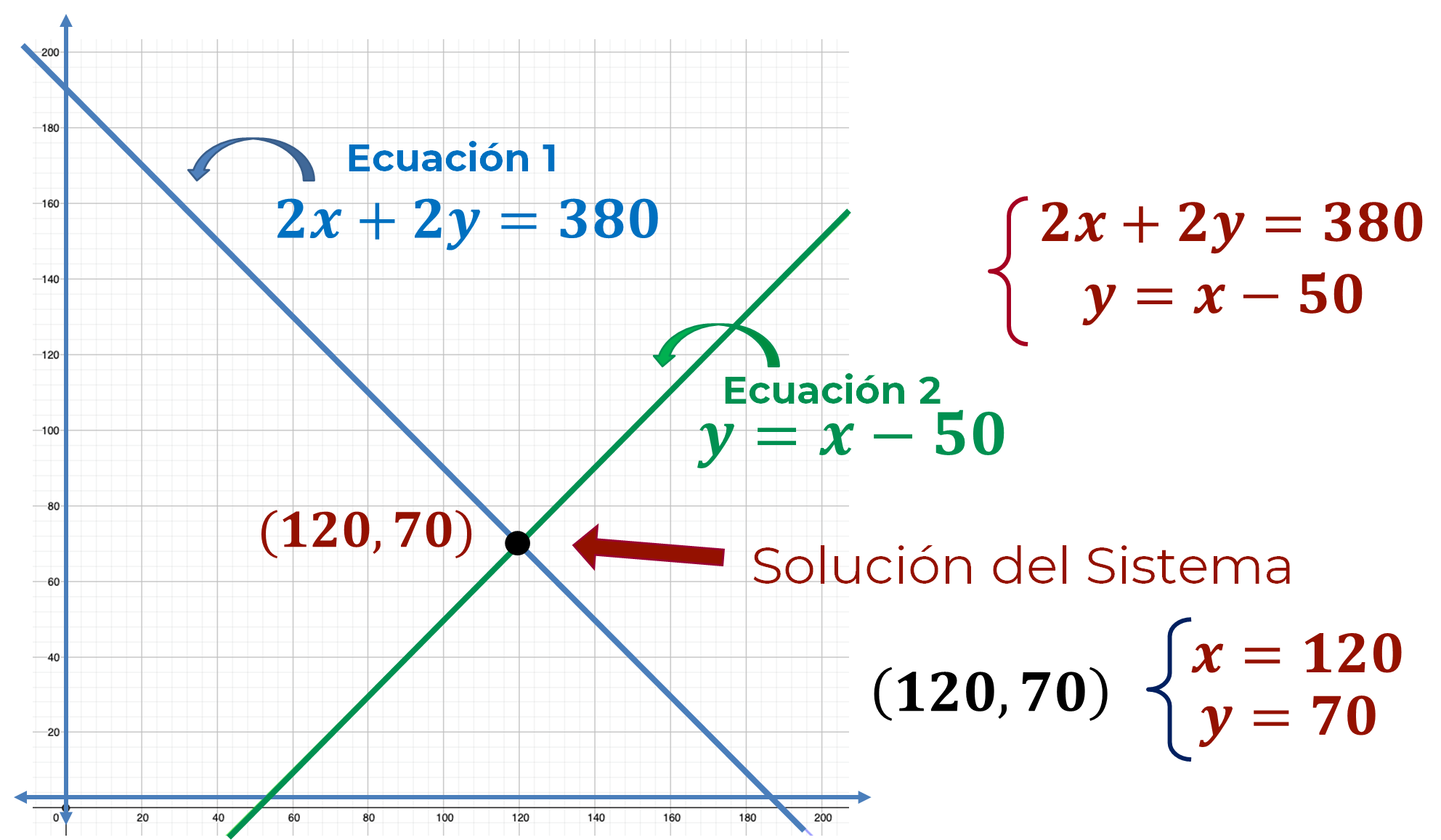
De esta manera, se identifica que el punto donde se intersecan las gráficas es (120, 70); que es la solución del sistema.

En este caso, el sistema tiene una solución única, ya que “x” = 120 y “y” = 70, son los únicos valores que satisfacen las dos ecuaciones del sistema.

Después de haber resuelto la situación-problema a través de un sistema de dos ecuaciones con dos incógnitas utilizando diferentes métodos, responde las siguientes preguntas:

¿Cómo te fue con cada método?

¿Descubriste algo nuevo al aplicar los métodos para resolver un mismo problema?

¿Qué método te pareció más eficiente para resolver el problema?

Un sistema de ecuaciones puede resolverse aplicando diferentes métodos, y siempre que se apliquen apropiadamente, llegarás a la solución del problema.

Sin embargo, puedes elegir un método de solución que resulte más conveniente, de acuerdo con las características que presenta cada ecuación.

También, la selección para utilizar un método de solución respecto a otro es la dificultad o facilidad que se tenga al despejar las ecuaciones, al aplicar las propiedades de los números y las operaciones, ya que en unos casos es más favorable y resulta más sencillo un método en comparación con otro.

Recuerda que, sin importar el método de solución utilizado, es indispensable comprobar los valores de las dos incógnitas, “x” y “y”, en ambas ecuaciones, para verificar que la igualdad se cumple.

Comprobación

Se comprueban los valores obtenidos en las dos ecuaciones sustituyéndolos en ambas ecuaciones del sistema.

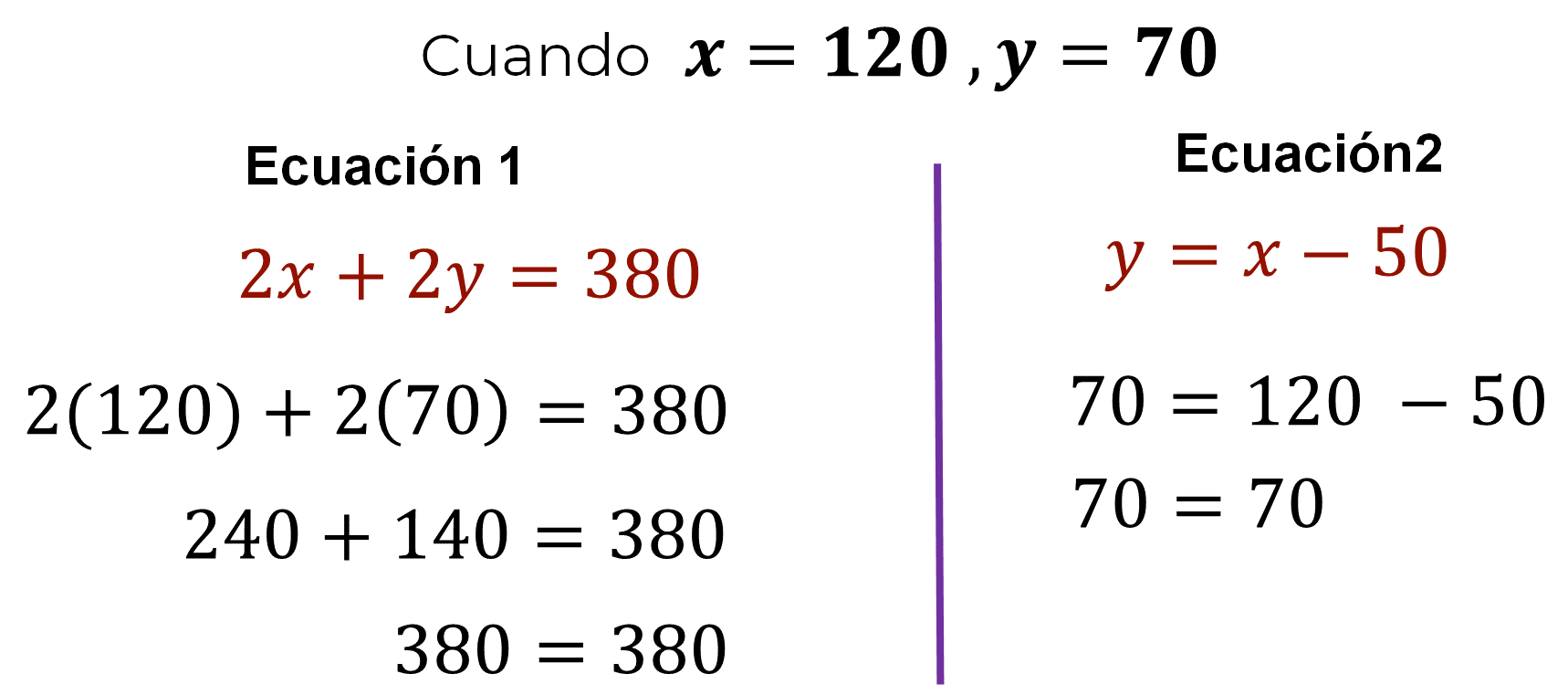
Se ha comprobado que la solución satisface la igualdad de las ecuaciones del sistema.

A continuación, revisa la siguiente situación-problema para que te ayude a elegir el método más conveniente de acuerdo con las características de las ecuaciones del sistema.

Situación-problema 2

Una empresa de focos ahorradores obtiene una ganancia por cada foco ahorrador que sale de ella y funciona de manera correcta, pero se produce una pérdida por cada uno que sale y está defectuoso. Un día en el que se fabricaron 2,100 focos, se obtuvo un beneficio de $968.80 por el total de focos en buen estado y defectuosos. 

• La ganancia por un foco en buen estado es de 60 centavos.
• La pérdida por un foco defectuoso es de 80 centavos.

¿Cuántos focos en buen estado se produjeron ese día? ¿Y cuántos focos defectuosos?

¿Consideras posible que sea mayor la cantidad de focos en buen estado que los defectuosos?

Antes de decidir y elegir el método de resolución para resolver el problema de los focos, es necesario plantear el sistema de ecuaciones, a partir de las condiciones que se establecen.

Analiza el enunciado del problema, con la finalidad de entender de qué trata, y establecer las relaciones entre los datos conocidos y las interrogantes. Después se traducirá a lenguaje algebraico lo que describe el problema.

Después de comprender el enunciado del problema, se desconoce la cantidad de focos en buen estado y la cantidad de focos defectuosos que se produjeron ese día; por esta razón la literal “x” representa los focos defectuosos, y la literal “y” representa los focos en buen estado; se iguala con 2100 que representa el total de focos producidos ese día en la fábrica.

De esta manera se forma el primer modelo matemático, es decir, la primera ecuación:

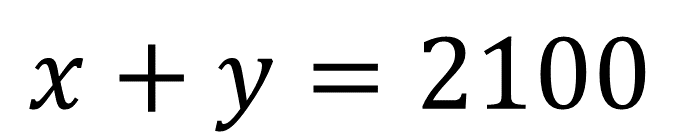
Para plantear la segunda ecuación, “x” representa la pérdida de los focos defectuosos, y en la literal “y” representa la ganancia de los focos en buen estado. Se escribe la ecuación de la siguiente manera:

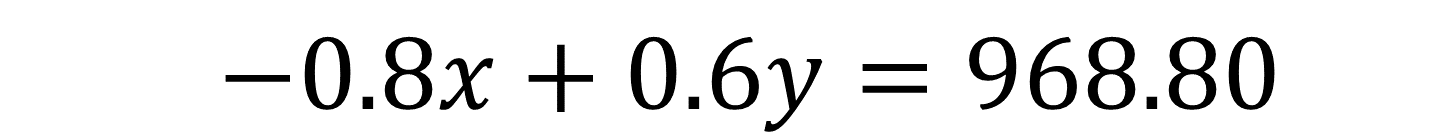
Las dos ecuaciones planteadas son ecuaciones lineales. De esta manera se establece el sistema de ecuaciones:

Para elegir el método de resolución, analiza la forma de las ecuaciones del sistema; observa que fácilmente se puede despejar a una de las literales de la ecuación uno, y así resolverlo por el método de sustitución.

También, puedes igualar los coeficientes de la incógnita que deseas reducir, y usar el método de suma y resta.

O podemos despejar la misma incógnita en ambas ecuaciones e igualar las expresiones, para resolverlo por el método de igualación, pero en este caso, implica un proceso más largo para llegar a la solución respecto al método de sustitución.

En cuanto al método gráfico, si se realiza con un recurso tecnológico, sería más rápido y sencillo. Pero en este caso es más complicado. Si tienes acceso a uno, puedes realizarlo por este método.

Con base en las características anteriores:

¿Qué método piensas que es conveniente utilizar?

Resuelve el sistema de ecuaciones mediante el método de sustitución. Recuerda que este método consiste en despejar una de las incógnitas, en cualquiera de sus dos ecuaciones y luego sustituir el despeje en la otra ecuación. De esta manera se obtiene una ecuación lineal que se resuelve permitiendo hallar el valor de una de las literales, para posteriormente encontrar el valor de la otra.

Método de Sustitución

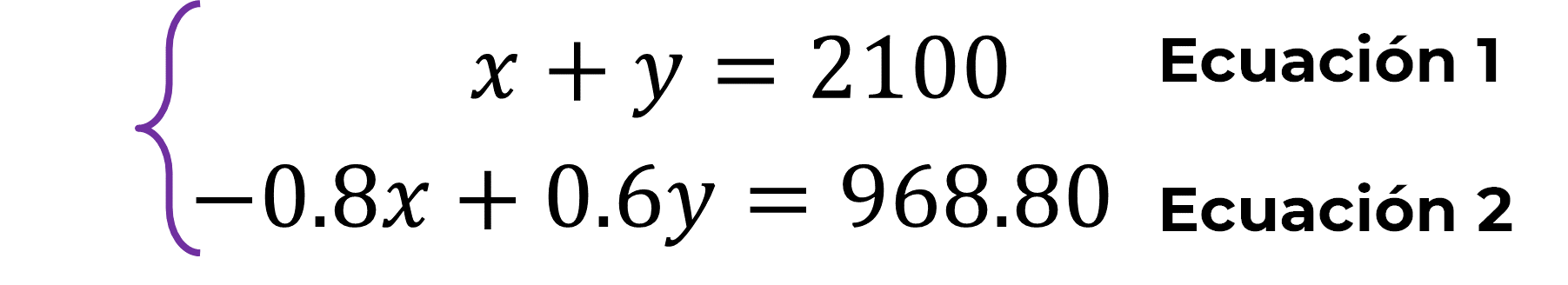
En la ecuación 1, se despeja la incógnita “y”.

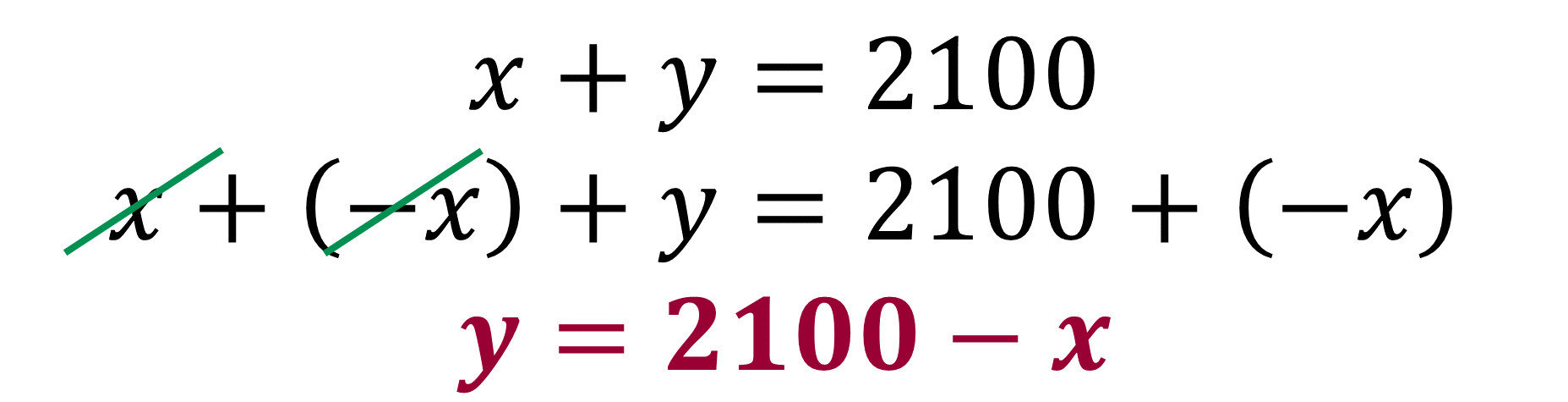
En la ecuación 1, la incógnita “y” quedó despejada.

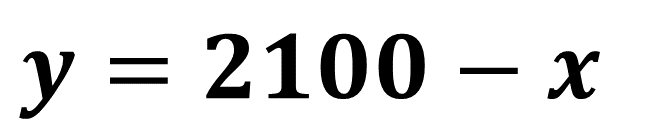
El despeje obtenido se sustituye en la ecuación 2.

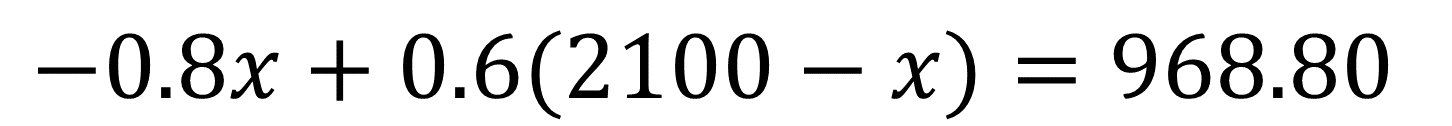
Se resuelve la ecuación de primer grado o ecuación lineal con una incógnita.

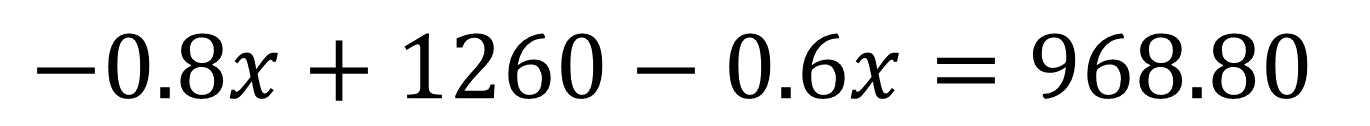
Se resuelve la ecuación de primer grado con una incógnita.

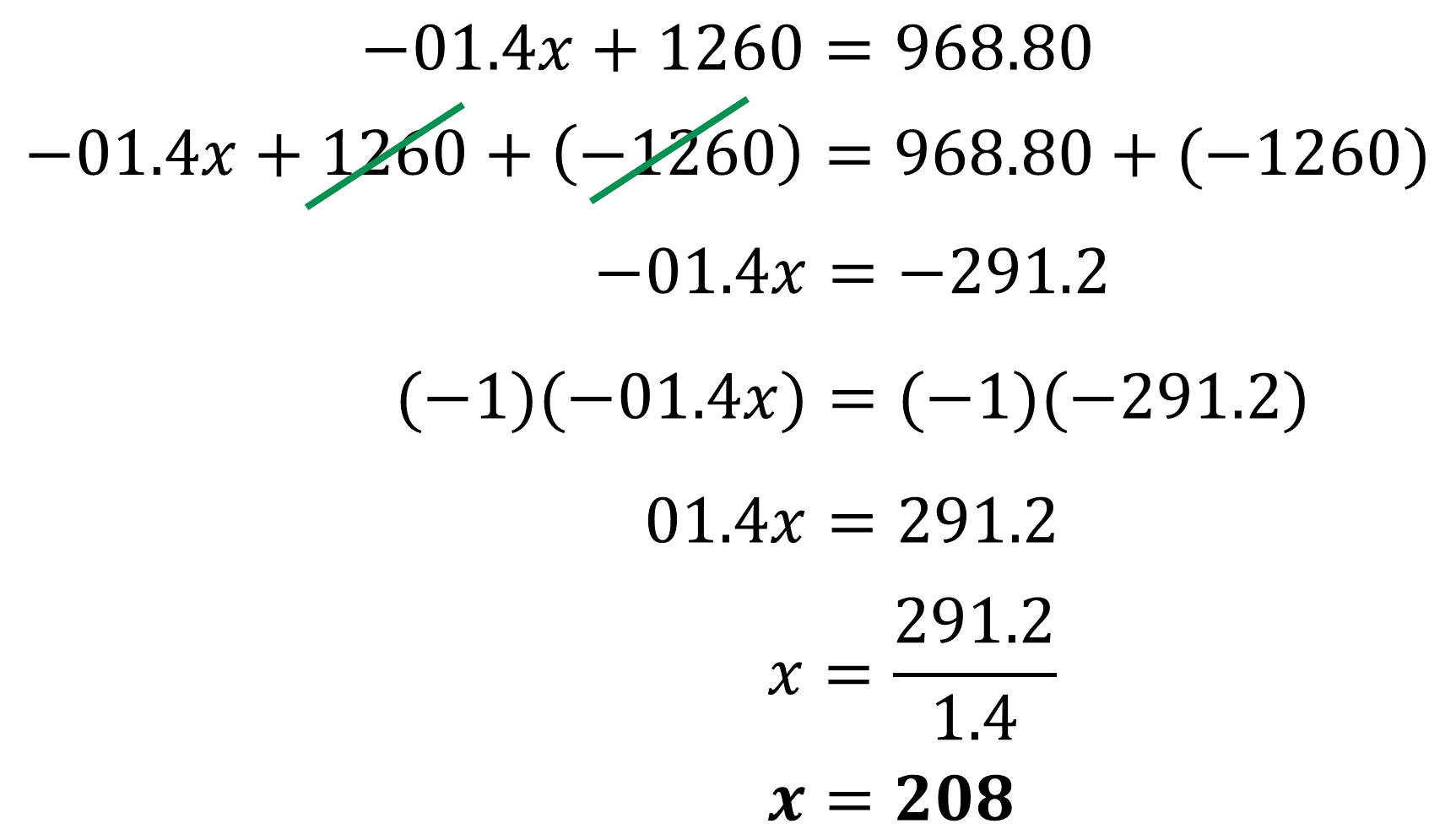
Se sustituye el valor encontrado, en este caso, en la ecuación 1, para encontrar el valor de la otra incógnita.

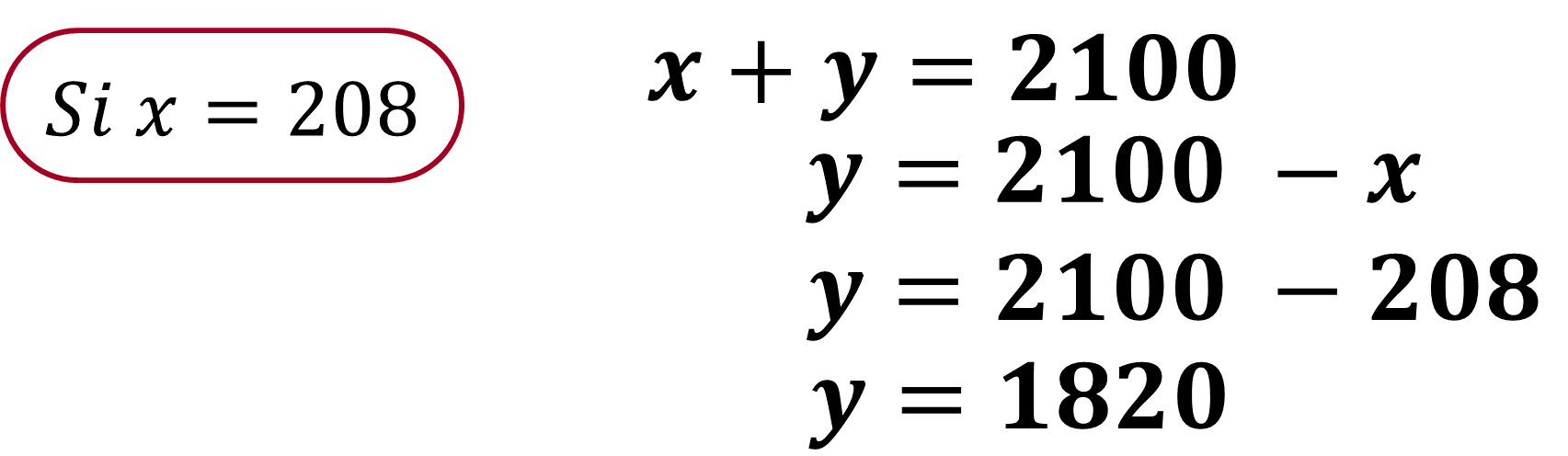
Los valores obtenidos son:

Comprobación. Se comprueban los valores obtenidos en las dos ecuaciones sustituyendo los valores encontrados en ambas ecuaciones.

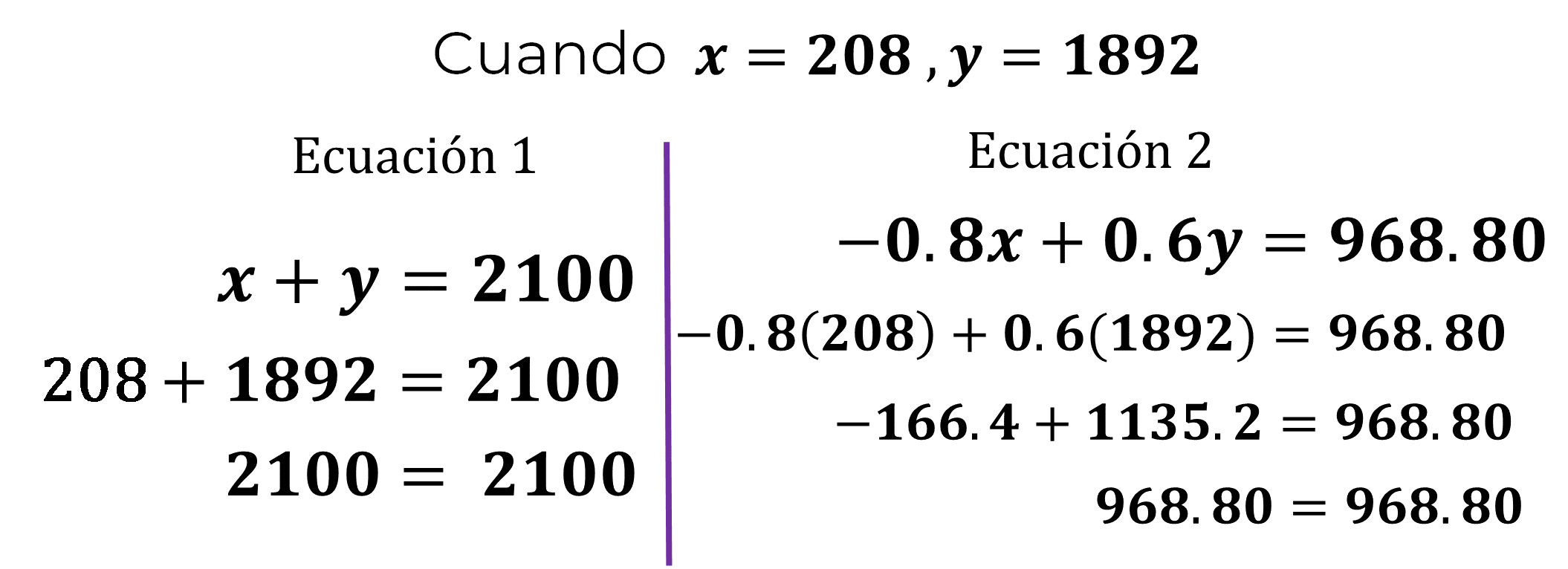
Después de resolver el sistema de ecuaciones y comprobar el resultado, ahora sabes que, en la fábrica se produjeron 208 focos defectuosos y 1892 focos en buen estado.

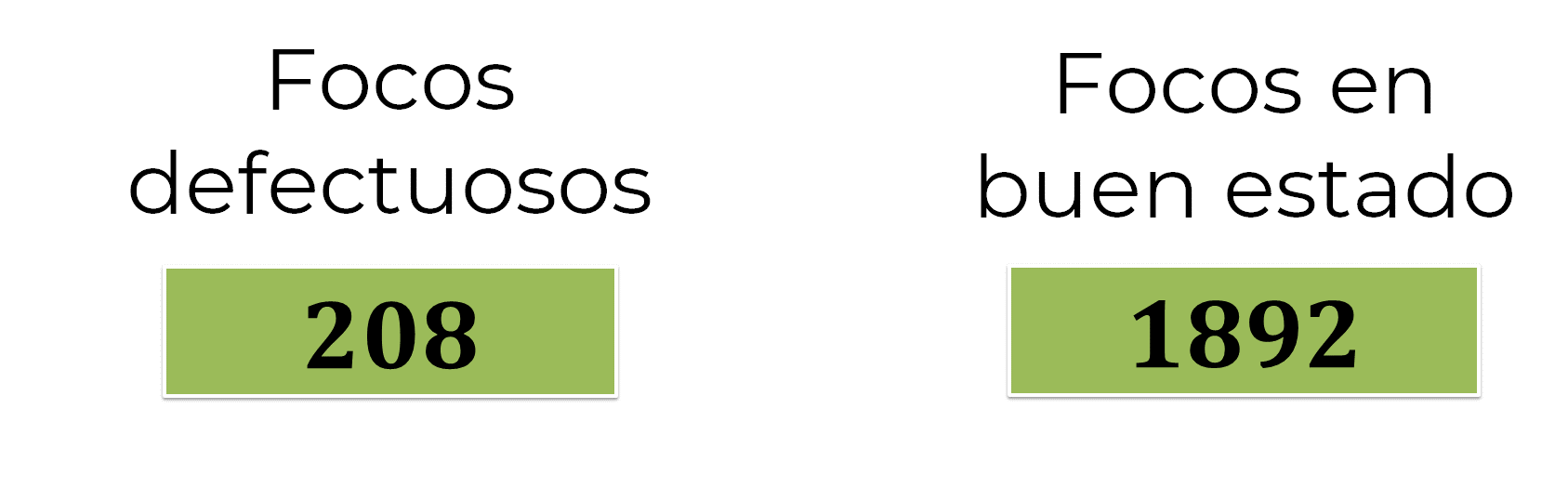
A continuación, analiza el siguiente sistema de dos ecuaciones con dos incógnitas, y argumenta con qué método de solución puede ser más práctica su resolución.

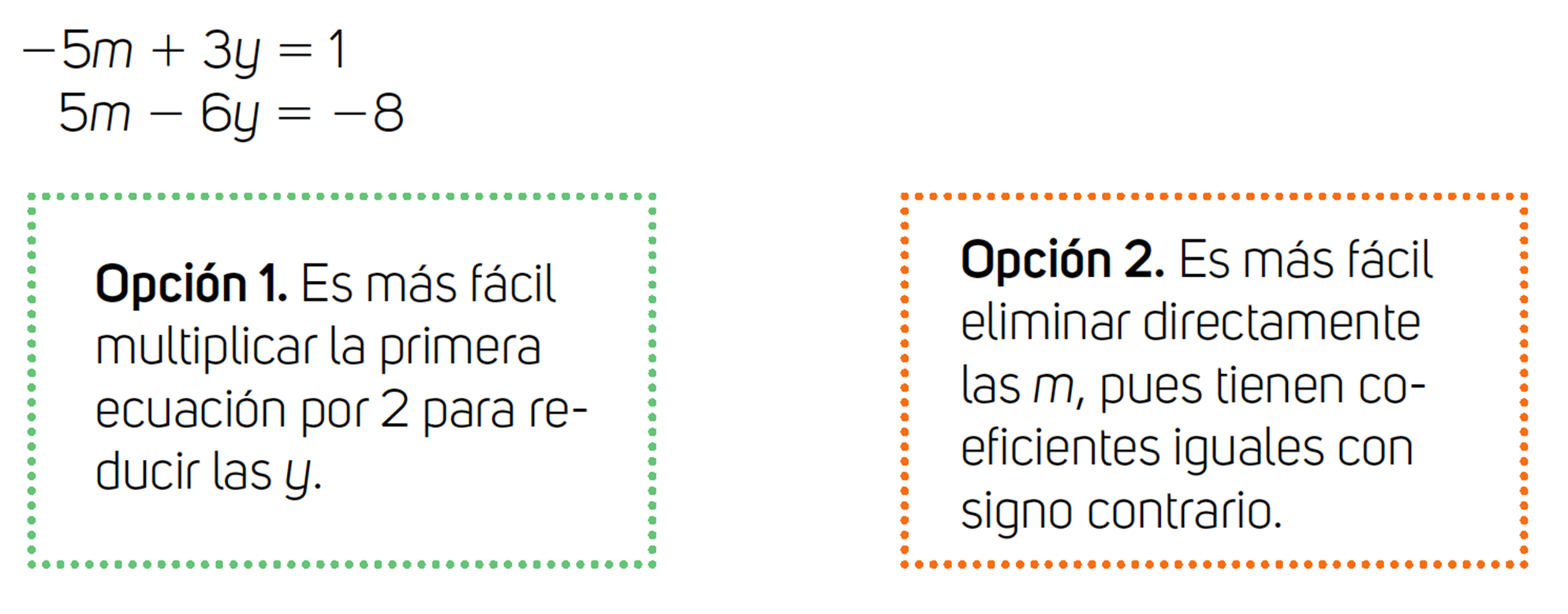
Analiza las opciones:

Opción 1. Si se multiplican ambos miembros de la ecuación -5m + 3y = 1 (por 2). Se obtiene -10m + 6y = 2. Y luego, se suman los términos semejantes de ambas ecuaciones. El realizar esta multiplicación para reducir la incógnita “y” en cada ecuación, lleva a realizar dos pasos.

Opción 2. Es más fácil eliminar directamente las “m”, pues tienes coeficientes iguales con signo contrario. Esta sugerencia te permite identificar que puedes reducir términos semejantes, y que puedes aplicar el método de suma y resta. Es decir, se realiza un paso menos respecto a la opción 1.

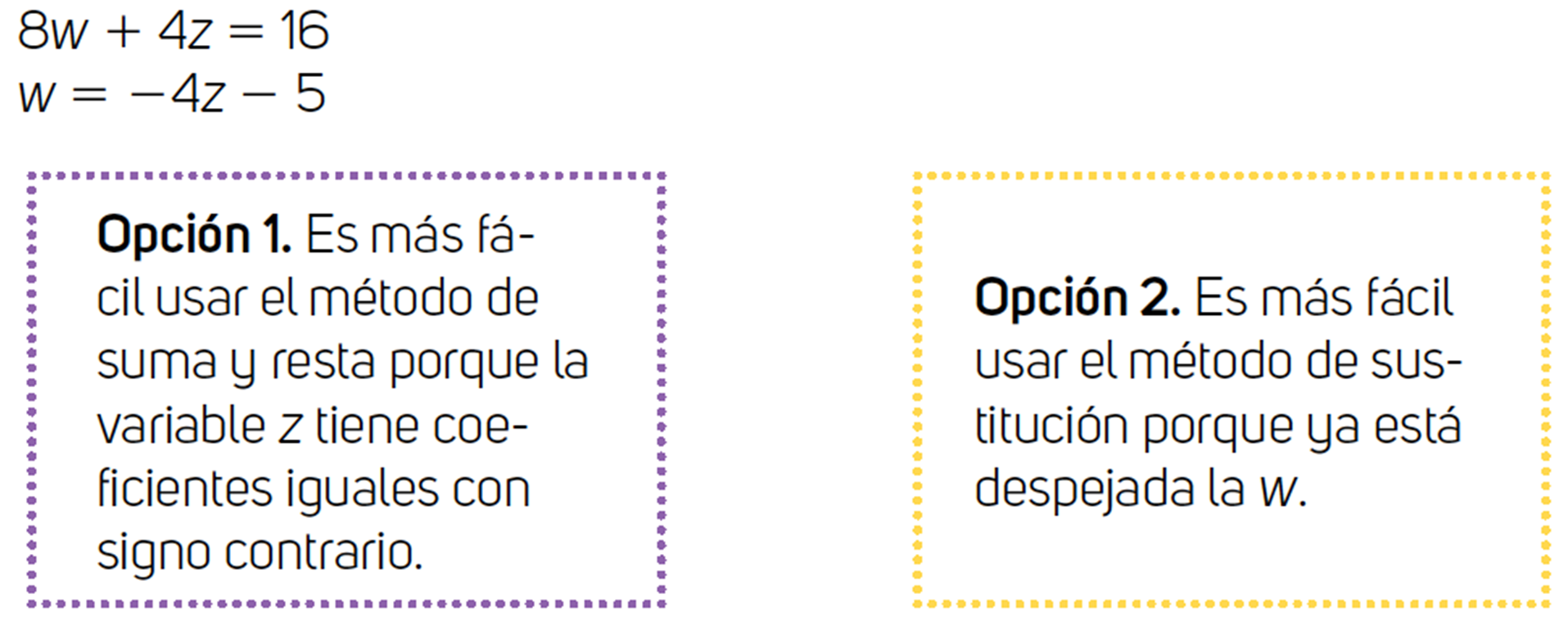
Ahora analiza un segundo sistema de dos ecuaciones con dos incógnitas y argumenta con qué método de solución puede ser más práctica su resolución.

Opción 1. Efectivamente si se decide usar el método gráfico, ayuda tener la incógnita despejada para tabular las ecuaciones y obtener los pares ordenados que representan los puntos en el plano cartesiano, pero este procedimiento requiere más tiempo. Puedes usarlo si te gusta graficar en el plano cartesiano, o si utilizas un recurso tecnológico para hacer las gráficas.

Opción 2. En el sistema de ecuaciones ya tienes despejada la misma incógnita, por lo que puedes igualarlas y formar una ecuación con una incógnita, la cual puedes resolver despejando la literal “x”. Por lo que puedes usar el método de igualación. Para este caso, este método puede facilitar su resolución de manera eficiente en comparación con el método gráfico.

Has revisado diversos sistemas de dos ecuaciones con dos incógnitas y has resuelto algunos. Además, analizaste sus características para determinar cuál método puede ser más práctico para obtener su solución. Sin embargo, en Matemáticas no hay métodos mejores que otros, pero sí más eficientes o prácticos.

En esta clase, revisaste la resolución de algunos problemas y profundizaste sobre cuál es el método más conveniente de acuerdo con las características de las ecuaciones del sistema.

Recuerda que una ecuación lineal o también llamada ecuación de grado uno, es una igualdad que involucra una o más incógnitas con exponente igual a uno, y no contiene productos entre ellas, es decir, una ecuación que contiene solamente sumas y restas de múltiplos constantes de una literal a la primera potencia.

Un sistema de ecuaciones lineales está formado por dos ecuaciones de grado uno, y encontrar la solución de un sistema de ecuaciones 2x2 significa obtener los valores de las dos incógnitas, es decir, que los valores hacen verdaderas simultáneamente ambas ecuaciones.

A lo largo de estas sesiones, has estudiado cuatro métodos para la resolución de sistemas 2 x 2:

• Gráfico. Se despeja la incógnita “y” en ambas ecuaciones y se asignan valores posibles para encontrar la coordenada del punto en que coinciden.
• Suma y Resta. Se busca eliminar una incógnita sin realizar despejes en la medida de lo posible.
• Sustitución. Se hace un despeje para sustituir en la otra ecuación.
• Igualación. Se despeja la misma incógnita de ambas ecuaciones para obtener una ecuación lineal con una incógnita.

Revisa y practica lo aprendido, puedes usar tu libro de texto de Matemáticas de segundo grado.

El reto de hoy:

Analiza el siguiente sistema de dos ecuaciones con dos incógnitas y argumenta con qué método de solución puede ser más práctica su resolución. Después, encuentra los valores de las incógnitas:

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/