El método de sustitución
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06El método de sustitución
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: resolver problemas mediante el planteamiento y resolución de sistemas de ecuaciones lineales con dos incógnitas utilizando el método de sustitución.
¿Qué vamos a aprender?
Conocerás cómo resolver problemas mediante el planteamiento y resolución de sistemas de ecuaciones lineales con dos incógnitas, utilizando el método de sustitución.
Anteriormente has reflexionado que un sistema de dos ecuaciones lineales con dos incógnitas está formado por dos ecuaciones de primer grado que están relacionadas entre sí mediante las dos incógnitas. Cada ecuación representa una condición o restricción del problema, por lo que, encontrar la solución significa obtener los valores de las incógnitas que resuelven, o hacen verdaderas, simultáneamente ambas ecuaciones.
En esta sesión, profundizarás en el método de sustitución para resolver problemas.
El método de sustitución para resolver sistemas de dos ecuaciones lineales con dos incógnitas consiste en despejar una de las incógnitas en cualquiera de las dos ecuaciones para sustituir el valor algebraico en la otra ecuación que forma el sistema.
Una vez resuelta, se calcula el valor de la segunda incógnita, y al final se comprueba que los valores numéricos de las incógnitas hacen verdaderas las dos ecuaciones.
¿Qué hacemos?
Reflexiona en lo siguiente:
¿Para qué te servirá aprender a resolver problemas que se modelan con un sistema de dos ecuaciones lineales con dos incógnitas?
Resolver una situación-problema de un sistema de ecuaciones lineales con dos incógnitas, es de utilidad para desarrollar el pensamiento matemático. También para plantearte desafíos que pongan a prueba lo que has aprendido, y para resolver problemas cada vez más complejos, ya sea en el contexto de las propias matemáticas o en el de las ciencias.
Un estudioso de las matemáticas, Nicolás Balacheff, dice en alguno de sus estudios: “es importante despertar en nosotros el deseo de certitud”, esto quiere decir, buscar la satisfacción intelectual, sentirnos felices por el solo hecho de saber que se encontró la solución correcta a un problema matemático. Es cubrir la necesidad de estar en lo correcto.
A continuación, analiza una situación-problema en la que emplearás un sistema de dos ecuaciones con dos incógnitas.
Situación-1.
En México como en muchos lugares del mundo, existen lugares a lo que se les llama deshuesaderos. En estos lugares se realiza la venta de refacciones y partes de diversos vehículos, como motos o automóviles, que tuvieron alguna colisión.
Martha lleva el inventario de un deshuesadero, y sabe que en el último semestre ingresaron 55 vehículos incluyendo automóviles y motos.
Ella sabe que el total de llantas de los 55 vehículos es de 170. Pero desconoce el número de automóviles y de motos que hay.
¿Cuántos automóviles y cuántas motos ingresaron en ese semestre al deshuesadero?
Resuelve la situación-problema planteada, para ello necesitas comprender el problema.
Se sabe que:
- La suma de automóviles y motos que entraron al deshuesadero ese semestre es igual a 55.
- La suma de todas las llantas es igual a 170.
- Cada automóvil tiene 4 llantas.
- Y cada moto tiene 2 llantas.
Para modelar la situación-problema con ecuaciones algebraicas para formar un sistema, realiza lo siguiente:
Representa la cantidad de automóviles con la literal “x”, y a la cantidad de motos con la literal “y”. Estas literales, “x” y “y”, serán las incógnitas.

En la segunda ecuación, se considera “4x”, ya que cada automóvil tiene 4 llantas y “2y” porque cada moto tiene 2 llantas.
Entonces el sistema de ecuaciones queda integrado como:
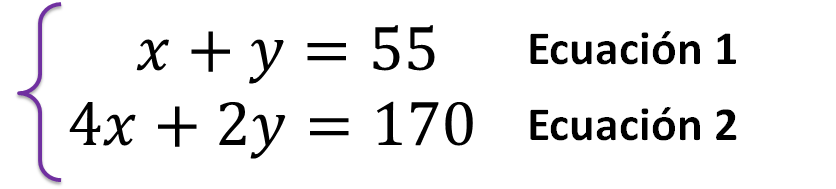
Para usar el método de sustitución en la resolución de la situación problema, realiza el despeje de una incógnita, en cualquiera de las dos ecuaciones.
Por lo tanto, se identifican 4 opciones posibles para iniciar la solución de la situación utilizando el método de sustitución.
Ecuación 1:
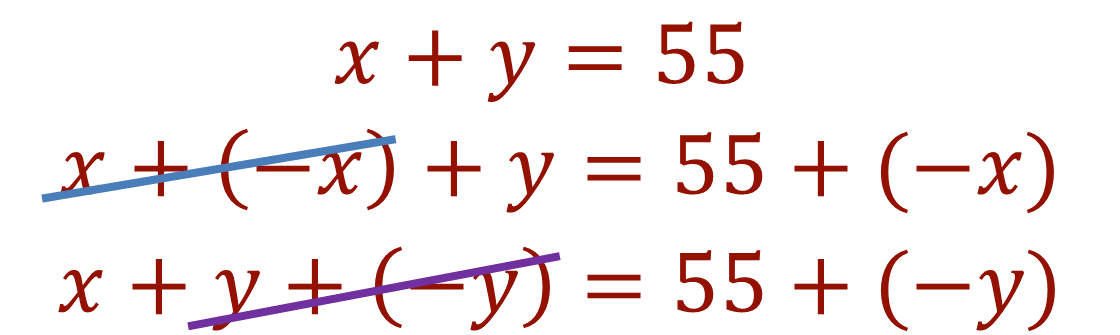
Se puede despejar cualquiera de las dos incógnitas que se tienen:
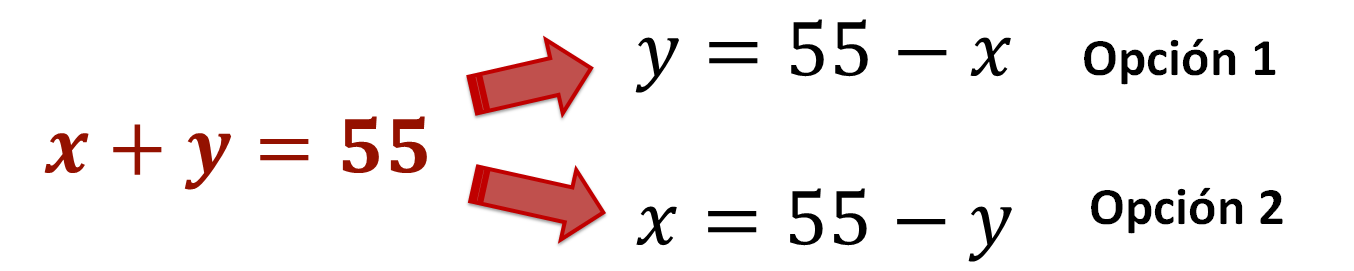
De esta manera se tiene: y = 55 – x, que es la opción 1. Y, x = 55 – y, que es la opción 2. Anota ambas opciones.
Ahora, presta atención en cuáles son las otras dos opciones para trabajar con el método de sustitución en la Ecuación 2.
Ecuación 2:
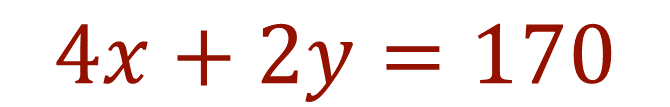
De la cual también puedes hacer dos despejes:
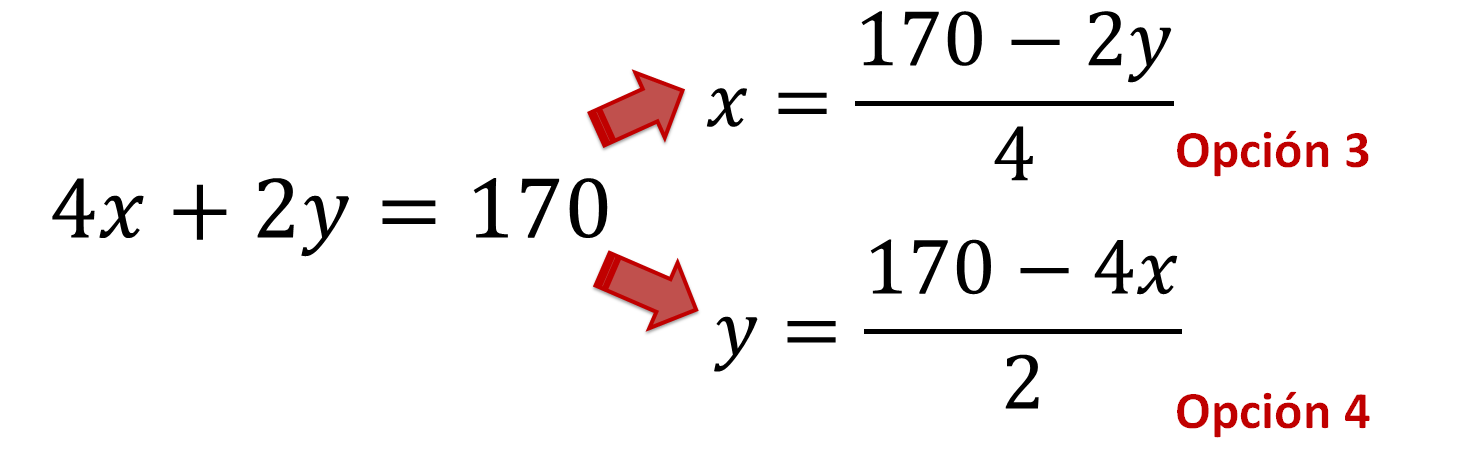
Ahora que tienes los 4 despejes o 4 opciones, puedes decidir con cuál de ellos trabajarás la sustitución, para poder dar solución al problema-situación.
Esta vez, trabaja primero con el despeje de “x”, de la Ecuación 1.
Es importante señalar que, para hacer la sustitución del valor algebraico de la incógnita elegida, debe realizarse en la otra ecuación, es decir, si se elige el despeje de una incógnita de la ecuación 1, se debe hacer la sustitución en la ecuación 2. De este modo tienes el despeje de la incógnita “x” de la Ecuación 1, por lo que realizarás la sustitución del valor algebraico en la ecuación 2.
El despeje de la incógnita “x” de la Ecuación 1 es:
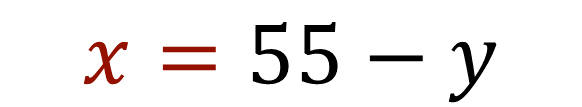
Este despeje será sustituido en la Ecuación 2:
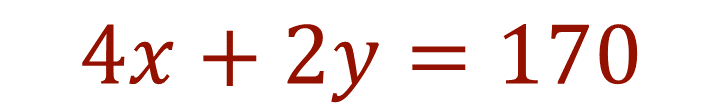
Obteniendo:

En el lugar de la incógnita “x” se anota el valor de la igualdad del despeje de “x” en la Ecuación 2.
Se realiza la multiplicación 4 (55-y) de la ecuación:
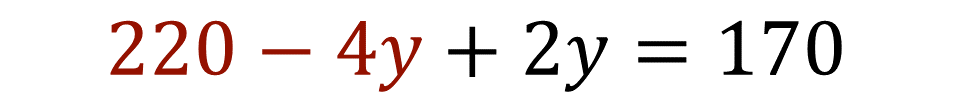
Utilizando las propiedades de los números y las operaciones, elimina el 220 del primer miembro de la ecuación al sumar su inverso aditivo, que es 200 negativo, en ambos miembros de la ecuación:
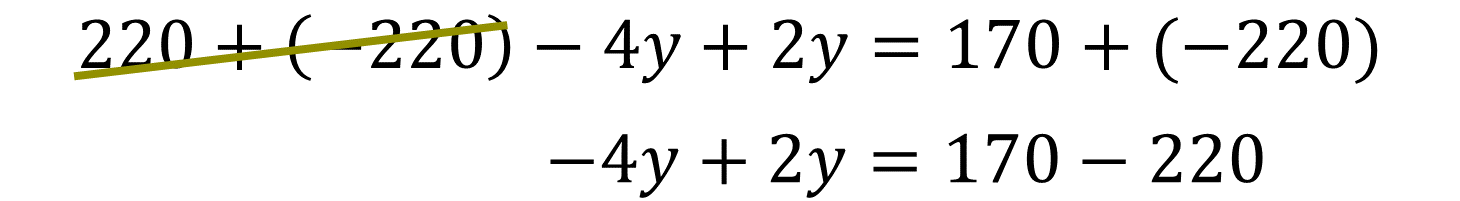
Reduce los términos semejantes:
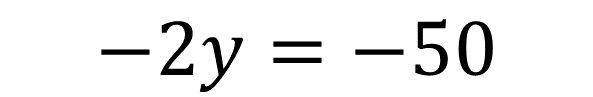
Si observas, tienes ambos miembros de la ecuación con valores negativos, para resolverla puedes multiplicar ambos miembros de la ecuación por -1 para operar con valores positivos. De este modo tienes que:
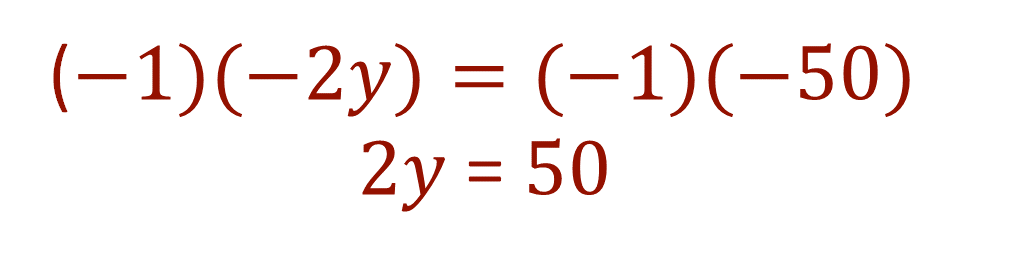
“Si 2 veces el valor de “y” es 50, ¿cuál será el valor de “y”?
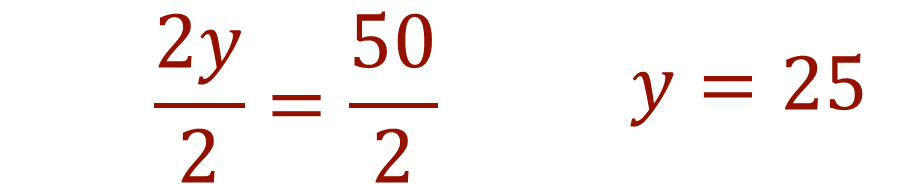
Al final tienes que y = 25
“y” representa la cantidad de motos que ingresaron al deshuesadero el primer semestre del año. Ahora Martha ya tiene esa información.
Una vez hecho esto, has hallado el valor de la incógnita “y” o bien, la cantidad de motos que ingresó al deshuesadero en el primer semestre del año, pero aún falta hallar el valor de la incógnita “x” o cantidad de automóviles que ingresaron al deshuesadero.
Para determinar el valor de “x”, sustituye ahora el valor numérico de la incógnita “y” en cualquiera de las dos ecuaciones, realiza la sustitución en la ecuación 1.
En lugar de escribir la incógnita “y”, escribe 25, que es el valor que has calculado. Entonces la ecuación queda de la siguiente manera:
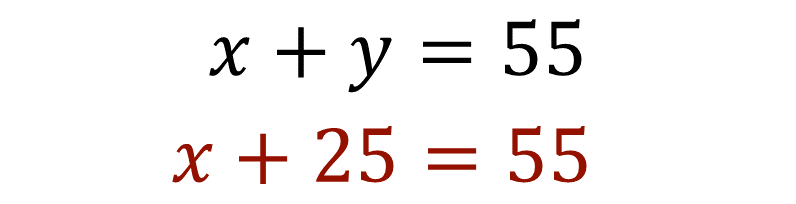
¿Cuál debe ser el valor de “x” para que al sumarle 25 el resultado sea 55?
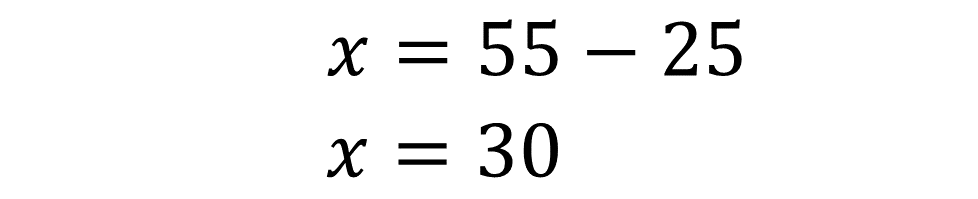
Por lo tanto “x = 30” y sabes que en el sistema de ecuaciones “x”, representa la cantidad de automóviles.
La cantidad de automóviles en el deshuesadero es de 30.
Para concluir con el método de sustitución, al igual que con cualquier otro método para resolver sistemas de dos ecuaciones lineales con dos incógnitas; comprueba los resultados.
Ya se conocen los valores numéricos de ambas incógnitas. Ahora, comprueba que se cumpla la igualdad de la ecuación.
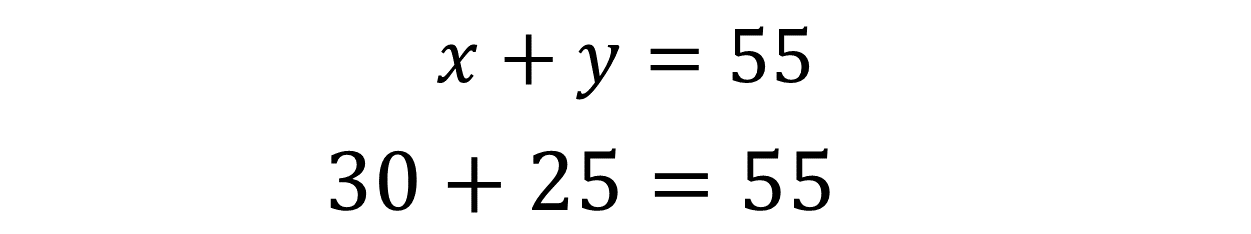
La ecuación con la sustitución queda de la siguiente manera:
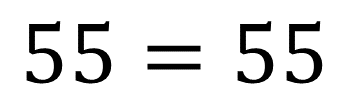
Ahora, comprueba con la ecuación 2:
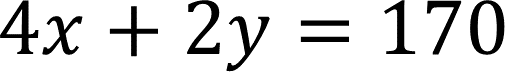
Realiza la sustitución de las incógnitas por los valores numéricos que representan. Por lo tanto, la ecuación queda:
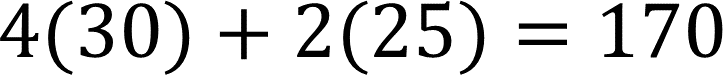
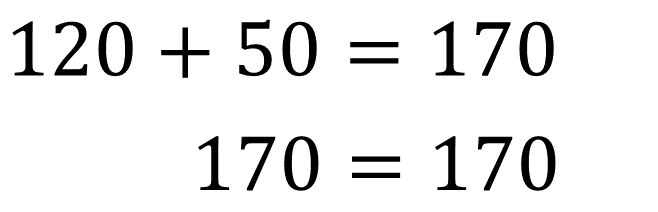
Recuerda que, si tienes alguna duda, puedes anotarla y consultar en tu libro de texto; o preguntarle a tu profesor de matemáticas.
Para fortalecer lo aprendido, resuelve otra situación-problema, mediante el planteamiento y resolución de un sistema de ecuaciones con el método de sustitución.
Identifica las incógnitas en la siguiente situación-problema:
Situación- 2.
Juan Carlos tiene $120 en monedas de $5 y $2, si tiene 33 monedas en total.
¿Cuántas monedas son de $5 y cuántas monedas son de $2?
Inicia con el análisis del problema.
- La suma de las monedas que tiene Juan Carlos son 33.
- La suma total de dinero es $120 pesos.
- Juan Carlos tiene monedas de $5 y $2 pesos.
Ahora plantearás el sistema de ecuaciones que modela la situación-problema.
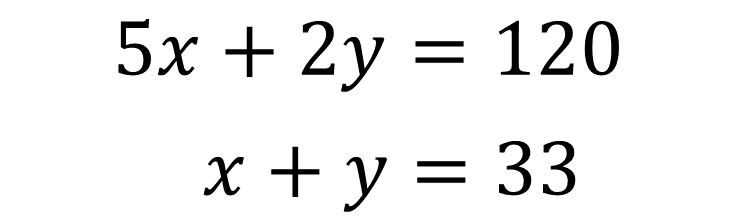
El sistema queda integrado como:

Ahora que tienes el sistema establecido, aplica el método de sustitución. En esta ocasión realiza el despeje de “y” en la ecuación 2.
Se despeja la incógnita “y” en Ecuación 2:
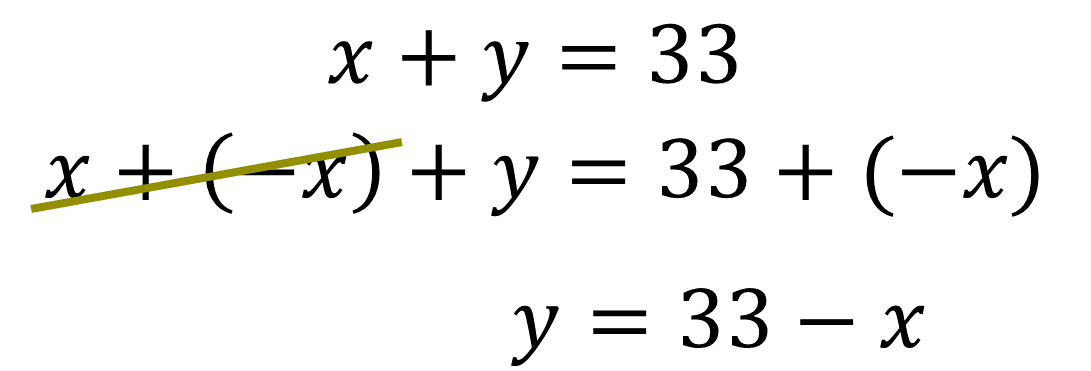
Una vez que tienes el despeje de la incógnita “y”, realiza la sustitución del valor algebraico en la ecuación 1, dado que se despejó la ecuación 2.
Trabaja con el despeje de “y” de la Ecuación 2:

Ahora sustituye en la ecuación 1 y obtienes:
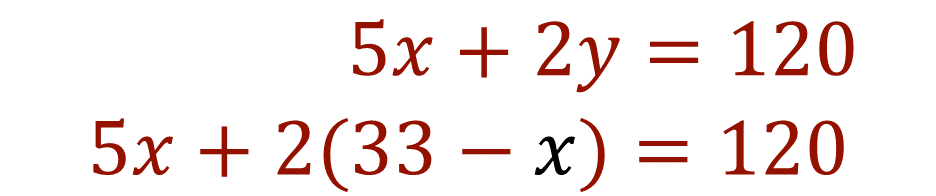
En el lugar de la incógnita “y” se sustituye el valor algebraico del despeje de “y” en la ecuación 1.
Al multiplicar 2(33-x) en la ecuación, obtienes:
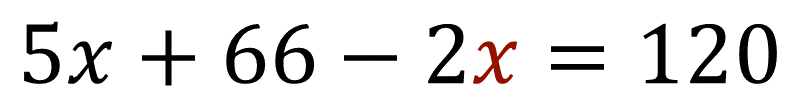
Resuelve aplicando las propiedades de los números y las operaciones inversas, suma en ambos miembros de la ecuación al inverso aditivo de 66, que es 66 negativo:
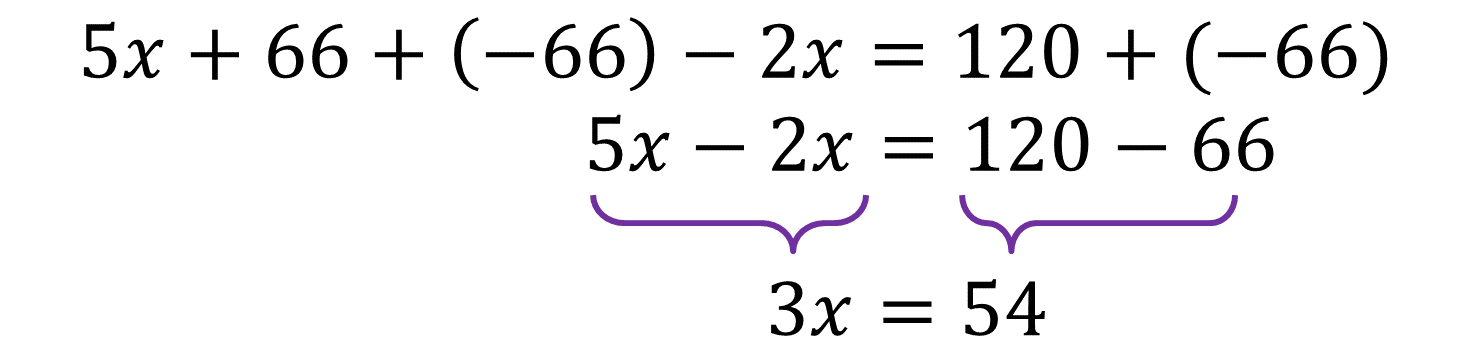
Para encontrar el valor de 3x=54, puedes hacer la siguiente interpretación:
¿Qué número multiplicado por 3 da como resultado 54?
Puedes calcular el resultado de dividir 54 entre 3 y el cociente es 18. Por lo que tienes:
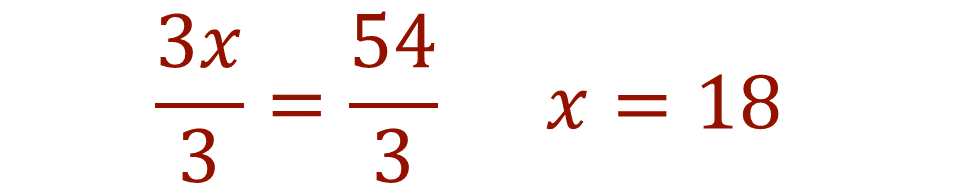
“x” representa la cantidad de monedas de $5 que tiene Juan Carlos.
Se sabe que: x=18
Ahora que ya sabes que Juan Carlos tiene 18 monedas de $5, puedes determinar cuántas monedas tiene de $2.
Para esto, realiza la sustitución de la incógnita “x” por su valor numérico en la ecuación 2.
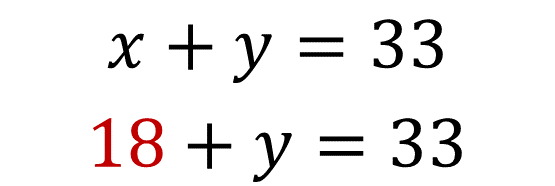
Resuelve la ecuación utilizando las propiedades de los números y las operaciones:
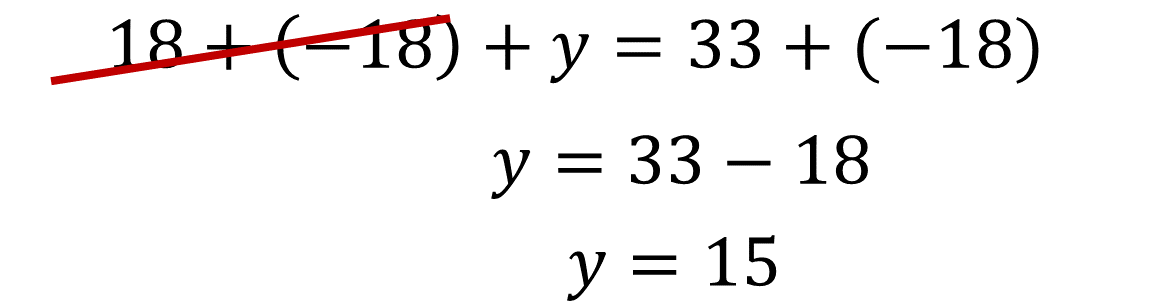
De este modo tienes que y=15, que en problema representa el número de monedas de $2 que tiene Juan Carlos.
A partir de los resultados, sabes que Juan Carlos tiene 18 monedas de $5 y 15 monedas de $2. Ahora, comprueba los resultados en ambas ecuaciones. Por lo que, tienes que revisar que se cumpla la igualdad de la ecuación.
Comprobar las soluciones.
La ecuación 1 es:
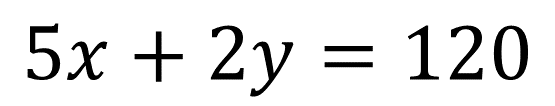
Se sustituye el valor numérico de ambas incógnitas en la Ecuación 1:
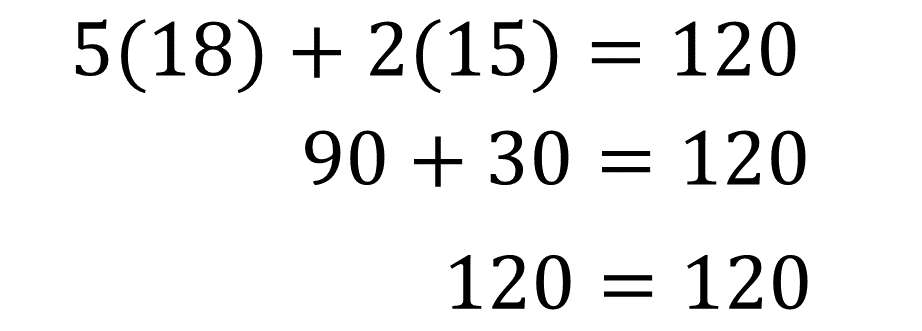
Es importante que los valores numéricos de las literales que eran incógnitas sean comprobados en las ecuaciones 1 y 2 del sistema de ecuaciones. Así que realiza lo mismo con la ecuación 2.
La ecuación 2 es:
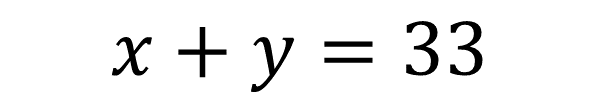
Se sustituye el valor numérico de ambas incógnitas en la Ecuación 2:
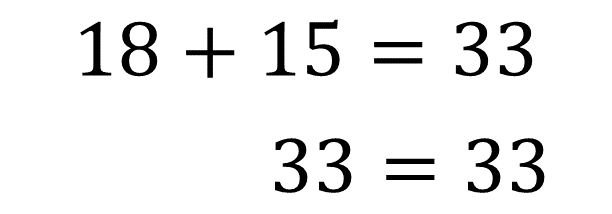
Para finalizar y seguir aprendiendo sobre este tema; leer la siguiente información que se encuentra en tu libro de texto, sobre este método de sustitución.
Método de Sustitución.
El método de sustitución consiste en despejar una incógnita de una de las ecuaciones y sustituir en la otra ecuación el valor hallado. De este modo se tiene una sola ecuación con una sola incógnita y se puede resolver despejando. Por ejemplo, en el sistema de ecuaciones:
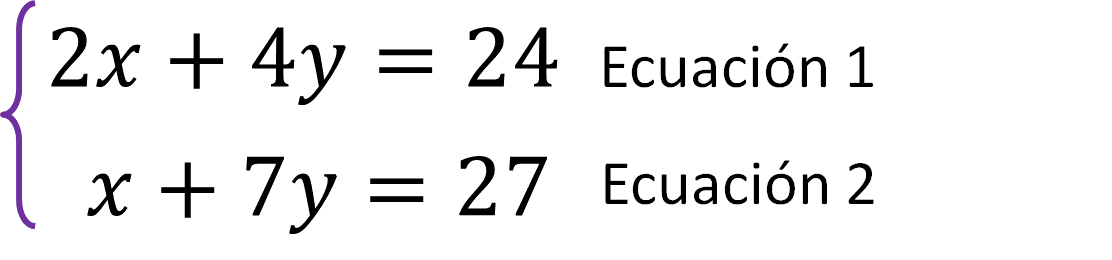
Despeja “x” en la segunda ecuación:
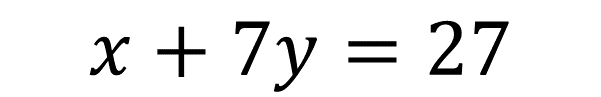
Sustituye esta expresión en la ecuación 1:
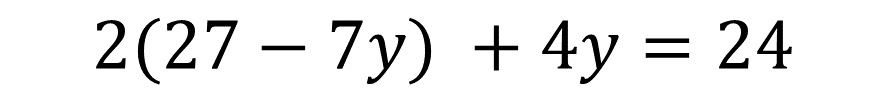
Realizando las operaciones y agrupando los términos semejantes obtienes la ecuación:
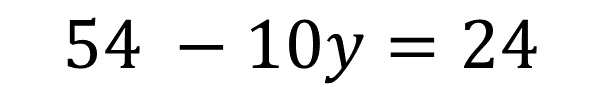
Cuya solución es:
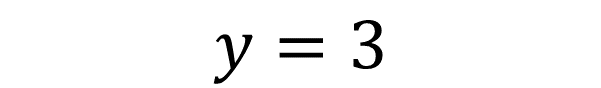
Ahora sustituye este valor en la segunda ecuación:
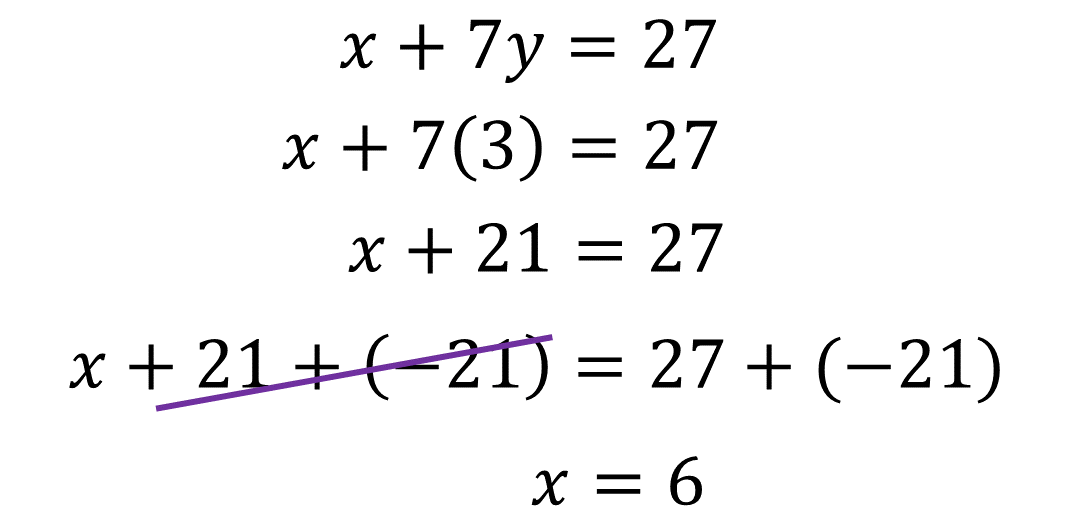
También se puede comenzar despejando primero la incógnita “y” sustituyéndola en la otra ecuación.
Para finalizar, lee las siguientes recomendaciones que pueden ser de utilidad para resolver un sistema de ecuaciones lineales con dos incógnitas.
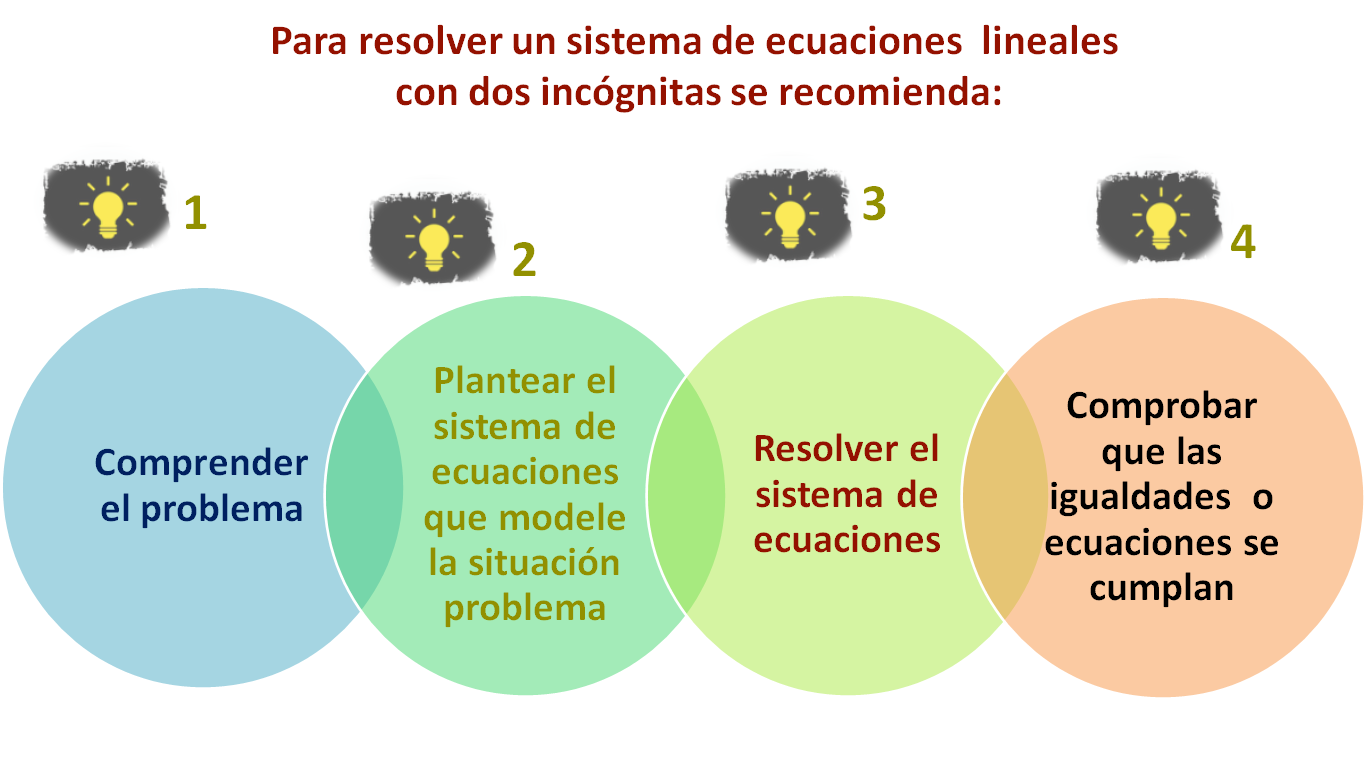
Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas en esta sesión.
El reto de hoy:
Consulta tu libro de texto de Matemáticas de segundo grado, en el tema de sistemas de dos ecuaciones lineales con dos incógnitas, y practica con los ejemplos propuestos en él.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion