Problemas de multiplicación con fracciones aplicadas en las escalas y otros contextos.

Problemas de multiplicación con fracciones aplicadas en las escalas y otros contextos.

Aprendizaje esperado: resuelve problemas de multiplicación con fracciones y decimales y de división con decimales.

Énfasis: conocer los significados de la multiplicación y aplicar el algoritmo usual de la multiplicación de fracciones.

¿Qué vamos a aprender?

Resolverás algunos problemas relacionados con el uso de la multiplicación, entre ellos la ampliación y la reducción. Confirmarás, a través del planteamiento de algunas situaciones, que la utilidad de las fracciones en la vida cotidiana es realmente importante y está presente más de lo que crees.

¿Qué hacemos?

Comenzaremos planteando la siguiente pregunta: ¿Alguna vez has visto los dibujos, planos o maquetas que usan en arquitectura?

Se utilizan para representar a escala la dimensión o medidas reales de un edificio, una casa, o el espacio a diseñar. En estos planos se incluyen las medidas de cada una de las partes que se van a construir o modificar, y para hacerlo se necesita conocer las medidas reales del espacio, para después reproducirlas en una maqueta o plano a escala.

La escala que más se utiliza por su practicidad es de 1 a 100 lo que significa que 1 cm. en el plano o maqueta representa 100 centímetros, o bien un metro en medidas reales. La escala es utilizada para mantener la proporción y para saber con precisión las magnitudes del espacio estudiado, por ejemplo: la distancia que habrá entre una pared y otra, a que altura se va a poner el techo. Y aunque no lo creas las medidas deben ser sumamente precisas, con milímetros.

Existen diferentes tipos de planos y la precisión dependerá de su uso, ya que pueden ser usados únicamente para mostrar la distribución de un espacio, pero si fueran utilizados para una remodelación, ampliación o una construcción, la elaboración de los mismos deber ser muy precisa; ya que si las medidas no son correctas podría representar pérdidas económicas y problemas en la ejecución. Se tiene que detallar desde el ancho de las columnas hasta el tamaño de las ventanas. Ahora veamos, cuál es la relación de esto con las fracciones y la multiplicación de las mismas.

Podemos decir que los planos de arquitectura están elaborados con base en representación del espacio a escala, es decir, 100 veces más pequeño, o bien mil veces más pequeño. En matemáticas, esta relación podemos escribirla en forma de fracción, o, en forma de razón. Cuando vemos un plano, en la parte inferior del mismo, siempre observaremos una línea como esta:

Cuando veas una referencia así, significa que un centímetro equivale a cien centímetros. Esta relación se puede escribir en forma de fracción, de la siguiente manera:

Para poder comprender mejor este concepto y sus elementos, observa el siguiente video del minuto: 00:00 a 00:33:

1. Reducción y escalas
   https://youtu.be/mDFWh6g83k8
   Ahora que ya conoces lo que es una escala, sus elementos y cómo se lee.
   Observa el siguiente video del minuto: 00:33 a 01:55 con un ejemplo, para que quede más claro:
2. Reducción y escalas
   https://youtu.be/mDFWh6g83k8
   Toma tu cuaderno y anota las siguientes preguntas a reflexionar:
   ¿Qué tipo de fracciones obtendrías, si es una escala de reducción?
   ¿Qué tipo de fracción obtendrían, si es una escala de ampliación?
   Ahora que ya conociste la fórmula para obtener una escala, ya sea de reducción o de ampliación en dos figuras -teniendo algunas de sus medidas-, te pudiste dar cuenta que:
   Cuando el objeto que se representa es más pequeño que el original, hablamos de una reducción y sería representada por una escala con fracción propia, es decir el numerador es menor al denominador.
   
   Y en el ejemplo 2 del vídeo pudiste observar que cuando obtenemos en la escala una fracción impropia, estamos hablando de una escala de ampliación-con el numerador mayor que el denominador-, la figura o dibujo a escala es más grande que el original.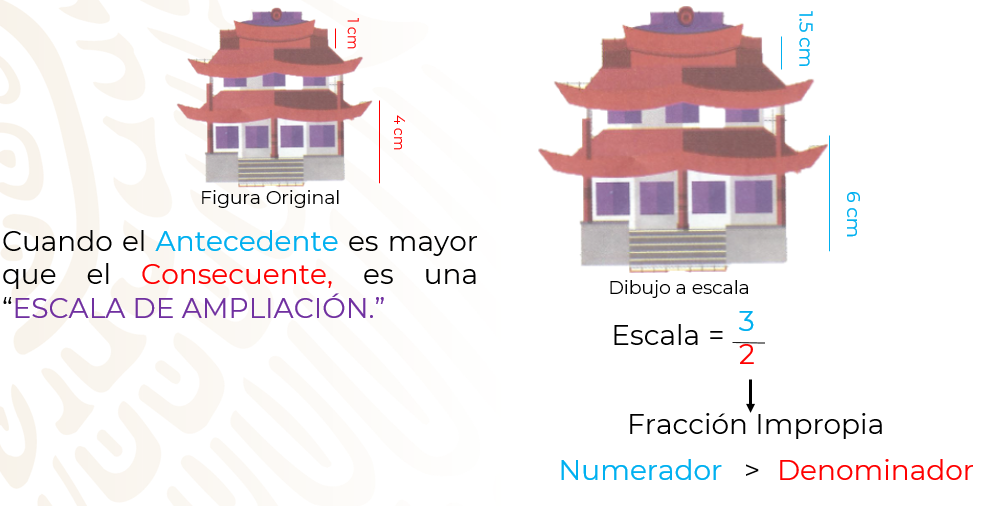
   
   Ya que tienes claro este concepto de escalas; recuerda que en la lección anterior estudiaste cómo multiplicar un número entero por una fracción, ahora verás cómo se resuelve un producto con dos fracciones. Observa el siguiente video del minuto: 00:22 a 03:10, presta mucha atención, para que después puedas resolver algunos ejercicios siguiendo el mismo procedimiento.
3. Interpretación gráfica de la multiplicación de fracciones
   https://youtu.be/UlVmfhKp270
   En el video se realizó un producto de fracciones propias y su producto se obtiene multiplicando numerador por numerador, y denominador por denominador. Haz uso de tu cuaderno para resolver algunos ejercicios:
   Multipliquemos las fracciones tres cuartos (3/4) y un tercio (1/3). Para ilustrar usaremos un rectángulo como el que se utilizó en el video anterior.
   Primero representaremos la fracción ¾. Para eso dividimos el rectángulo en 4 partes iguales, posteriormente, marcamos o coloreamos 3. Enseguida dividimos, de manera vertical, el rectángulo en tres partes iguales, y marcamos 1 ¿En cuántas partes quedó dividido el rectángulo?
   
   Ese será el número que colocaremos en la parte del denominador. La respuesta es tres doceavos
   Recuerda que la multiplicación de fracciones se resuelve multiplicando directamente el numerador por el numerador y el denominador por denominador. Observa que tenemos el mismo resultado:
   
   Es probable que te haya surgido la duda de ¿Cómo multiplico una fracción propia con una fracción impropia? Para eso, observa el siguiente video del minuto: 03:11 a 05:15
4. Interpretación gráfica de la multiplicación de fracciones

https://youtu.be/UlVmfhKp270

Tomando en cuenta lo que observaste en el video, resuelve la siguiente operación:

Siete cuartos por dos quintos. 7/4 x 2/5

Anotamos siete cuartos (7/4), lo que significa tener dos enteros, ya que la fracción es impropia, posteriormente los dividimos en 4 partes iguales, en forma horizontal, y coloreamos 7 fragmentos. Posteriormente, para representar la fracción dos quintos, dividimos ambos enteros en cinco partes iguales y sombreamos cada uno, dos de las 5 columnas. Contamos las partes marcadas con ambos colores y obtenemos: 14 veinteavos

Ahora multiplicamos directamente numerador por numerador y denominador por denominador

Ahora que ya sabes qué es una escala y cómo realizar un producto de fracciones, anota en tu cuaderno las siguientes preguntas para reflexionar:

• ¿Por qué las escalas están relacionadas con las fracciones?
  Están relacionadas ya que su representación está determinada por una razón geométrica. La escala es igual a: la relación entre el valor del antecedente entre el valor del consecuente, y en este caso, se expresa con número decimal.
  
• ¿Cómo podríamos construir una figura a escala, aplicando un producto de fracciones?

Para responder esta pregunta usemos de ejemplo el siguiente ejercicio:

El objetivo es calcular las medidas de una casa, a partir de sus medidas originales aplicando la escala de reducción.

¿Cuál sería la medida de la altura del techo? Para poder conocerla tenemos que obtener el producto de la medida con la escala, es decir, multiplicar la altura del techo 7/2 por la escala 1/2 de este modo obtenemos como resultado: siete cuartos (7/4), para la medida del techo a escala.

En la imagen, puedes observar que la fracción siete cuartos es la mitad de siete medios.

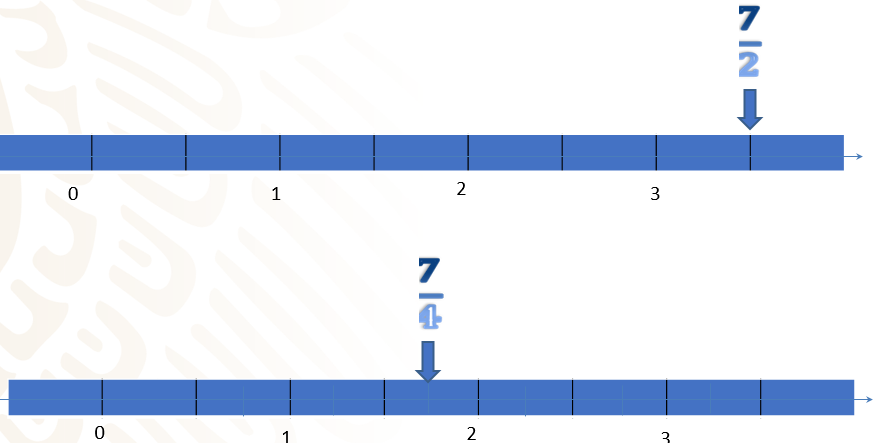
Veamos otra representación gráfica donde se observa como 7/4 es la mitad de 7/2.

Muy bien, ahora calcula la medida de las ventanas. Como puedes ver, son circulares.

Primero: Identifica la medida del radio.

Posteriormente, aplica la escala, multiplicando como en el ejercicio anterior.

Continúa con las medidas faltantes de la casa. Y recuerda: la escala que se está utilizando es la de un medio.

No olvides que para lograr encontrar las medidas correctas hay que multiplicar la medida original por la escala.

Ahora veamos otras situaciones donde la multiplicación de fracciones es sumamente importante. Analiza la siguiente situación:

Al llegar a un establecimiento de alimentos, nos ofrecieron un recipiente, el cual nos indicaron, tenía una capacidad de 1 ¾ litros de agua.

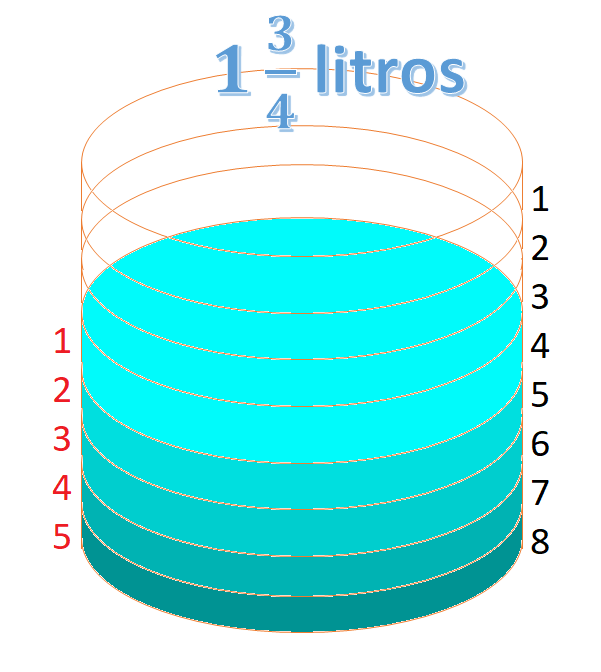
Aunque por las marcas observamos que, de líquido, tiene únicamente cinco octavos de su capacidad. La pregunta es ¿Qué cantidad de agua tendrá dentro?

Probablemente ya estés imaginando que la operación que puedes hacer es una multiplicación. Esto lo sabes porque si tuviéramos dos botellas completas de agua de la misma capacidad, y quisiéramos saber cuánta agua tenemos en total, únicamente multiplicaríamos por 2. Ahora al calcular el resultado, el procedimiento es el mismo, es decir, multiplicar el valor total del recipiente por la fracción. Recuerda que un número mixto “Es aquel que se compone de un número entero y una fracción”, por lo tanto, este número mixto puede ser representado como una fracción impropia. Y para reescribir el número mixto a fracción impropia, recuerda que debes seguir el siguiente procedimiento:

Primero identifica al número entero y la fracción propia, posteriormente debemos multiplicar el número entero -que es el número 6 por el denominador que es el número 2-, así tenemos que 6 x 2 es igual a 12. Ahora a 12 le sumaremos el numerador que es 1 y tenemos que el resultado es igual a 13 y el denominador seguirá siendo 2, por lo que la fracción impropia es trece medios.

Después de convertir el número mixto a una fracción impropia podremos realizar el producto de fracciones, multiplicando numerador por numerador y denominador por denominador. Resolvamos entonces el problema del recipiente de agua:

Al convertir el número mixto 1 entero 3 cuartos, obtenemos la fracción impropia 7 cuartos (7/4).

Ahora esta fracción la multiplicaremos por la cantidad de agua que hay en el recipiente, 5 octavos (5/8), obteniendo el resultado de 35 treintaidosavos (35/32), o expresado en número mixto: un entero tres treintaidosavos.

Multiplicando podemos obtener la cantidad de agua, y por supuesto esto sucede en contextos similares. Ahora toma tu cuaderno y trabajemos con las siguientes situaciones:

Problema 1: Una caja dice contener tres cuartos kilogramos de azúcar, pero sólo tiene un quinto de su capacidad: ¿Cuál será su contenido de azúcar?

Para poder resolverlo multiplicaremos los tres cuartos (3/4) de kilo gramos de azúcar por la quinta parte (1/5) de la capacidad. Por lo que 3 X 1 = 3, y 4 x 5 = 20. Así que el contenido de azúcar que tiene la caja es igual a: tres veinteavos (3/20).

Problema 2: En mi fiesta de cumpleaños compartí con mis amigos un pastel y me sobraron tres quintas partes, al siguiente día mi prima se comió la séptima parte de lo que sobró. ¿Qué fracción del total se comió ella?

Para poder resolverlo multiplicaremos las tres quintas partes (3/5) que sobraron del pastel por la séptima parte (1/7) que se comió al día siguiente. Por lo que 3 x 1 = 3, y 5 X 7 = 35. Como resultado, la fracción de pastel que se comió mi prima fue de: 3/35.

Problema 3: Tengo sesenta botellas de agua de un cuarto de litro y quiero saber ¿Cuántos litros de agua tengo? Ya que iremos a acampar por varios días.

Para resolverlo multiplicaremos las sesenta botellas, -recuerda que cuando multiplicas un número entero por una fracción puedes colocar debajo del entero la unidad-. Posteriormente podemos ya multiplicar por la cuarta parte de la capacidad de cada botella, por lo que 60 X 1 = 60 y 1 X 4 = 4; dándonos 60/4, que es igual a 15 enteros. De este modo obtenemos: quince litros de agua, como resultado.

Para finalizar te presentamos las medidas que debiste obtener de la casa a escala. Compáralas con las tuyas, para ratificar que estén correctas.

Como lo observaste, la multiplicación de fracciones es de utilidad, ya que podemos obtener escalas y resolver una inmensa cantidad de problemas de distintas situaciones.

Nunca te olvides que, al multiplicar fracciones se hace numerador por numerador y denominador por denominador.

El reto de hoy:

Revisa en tu libro de texto el tema: “identificación de fracciones y decimales” y realiza las actividades que ahí se sugieren.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/