El rango y la media.

Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) el rango y la desviación media de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión.

Énfasis: establecer el rango de un conjunto de datos para analizar su dispersión. Analizar como la media se afecta por valores atípicos.

¿Qué vamos a aprender?

En esta sesión estudiarás el aprendizaje esperado: “Usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) el rango y la desviación media de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión.”

Aprenderás cómo establecer el rango de un conjunto de datos para analizar su dispersión. También analizarás como la media se afecta por valores atípicos.

¿Qué hacemos?

La humanidad utiliza los conocimientos sobre matemáticas en muchas situaciones de la vida. Ya sea en las actividades cotidianas en casa, en el trabajo o en la escuela. También en los ámbitos científicos y tecnológicos, etc. La organización, análisis y representación de los conjuntos de datos es algo gusta mucho. Para representar un conjunto de datos se utilizan medidas de tendencia central y de dispersión. ¿Cuáles medidas de tendencia central conoces?

Observa el siguiente audiovisual que describe brevemente las características de estas medidas de tendencia central y por qué son útiles.

Observa del minuto 00:50 al 01:58.

1. ¿Cómo cambia la media aritmética?
   https://youtu.be/sLEu_Cv2fCM
   En esta lección centrarás el estudio en la Media aritmética o promedio. Ésta se calcula sumando el valor de todos los datos de un conjunto y luego dividiendo entre el número de datos contenidos en el conjunto.
   Se usa mucho esta medida de tendencia central en la escuela. Por ejemplo, cuando se busca representar con un solo valor numérico a todos los datos de evaluación obtenidos en un periodo escolar. ¿En qué otra situación se usa el promedio o media aritmética?
   Por ejemplo:
   El profe Enrique y sus alumnos, usaron una aplicación para celular y pidieron 4 platillos, las bebidas ya las tenían, así se comparte la comida a manera de buffet. Como usaron el celular para hacer el pedido, al momento de dividir la cuenta sumaron el costo de cada platillo y lo dividieron entre 4. Después cada quien me hizo una transferencia electrónica con su aportación. Esto es hacer un promedio.
   Para este caso además de ser un reparto equitativo en estas condiciones es coincidente a la obtención de la media aritmética o promedio para encontrar un valor representativo del conjunto de datos, en este caso, el costo representativo de los alimentos.
   Sin embargo, no siempre es así.
   En ocasiones se confunde el cálculo del promedio o media aritmética con el cálculo del reparto equitativo.
   Es importante que comprendas que el promedio es la suma del valor de todos los datos dividida entre el número de datos del conjunto. En el caso del profesor Enrique, coincidió el número de platillos con el número de comensales. Pero esto no siempre así. Pudieron comprar más de cuatro platillos, 7 por ejemplo. Dado que tendrían un buffet. Para hacer un reparto equitativo entonces se divide entre 4 porque son 4 comensales, pero para el promedio se dividiría la suma de los costos entre 7, que es el número de platillos.
   Así que, analiza muy bien sus datos para saber cómo calcular un promedio no sea que hagan el cálculo de un reparto equitativo en lugar del cálculo de la media aritmética.
   En las aplicaciones electrónicas de comida o de localización geográfica aparece una clasificación de qué tan caros o baratos son los productos o servicios de un lugar, como una cafetería, por ejemplo. Para conocer el valor representativo de un conjunto del valor de los platillos vendidos se puede usar la media aritmética.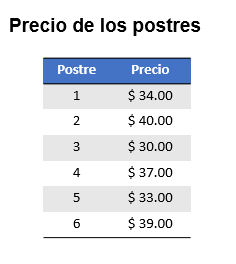
   
   Por ejemplo, si una cafetería sirve 6 postres con los siguientes precios: $34, $40, $30, $37, $33 y $39.
   
   Puedes calcular el promedio sumando todos los precios y luego dividiendo entre el número de postres ofrecidos. La media o promedio usualmente se representa con una x con testa, que es una línea sobre la letra. Así que… 34 + 40 +30 + 37 + 33 + 39 es igual a 213, que al dividirlo entre 6, es decir, el número de postres disponibles se obtiene: 35.5.
   Esto significa que 35.5 pesos es la media aritmética y se puede considerar como el valor representativo del precio del conjunto de postres.
   Si se compara el precio promedio de los postres con el salario mínimo actual, podría clasificarse como un precio caro o barato.
   Esta clasificación se puede obtener haciendo uso de la media aritmética y contrastando este valor con lo que una persona gana en su trabajo. Creo que para quienes ganan más del salario mínimo no es un postre caro, pero tal vez para quienes ganan el salario mínimo no es barato.
   Usar la media aritmética es muy útil, sin embargo, hay que tomar algunas precauciones como la que se ha mencionado. Además, dependiendo del conjunto de datos, la media puede verse afectada y no ser considera como representativa.
   Reflexiona dos situaciones: ¿Qué pasaría si por un lado existen valores atípicos o bien, por el contrario, aparecieran datos repetidos en el conjunto?
   Haz algunos cambios al ejemplo y observa los posibles efectos en el valor de la media.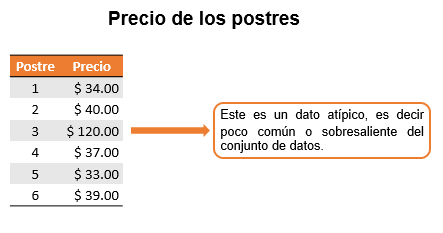
   
   Primeramente:
   Si los precios de los seis postres ahora fueran: $34, $40, $120, $37, $33, $39, ¿cuál sería la media? ¿Crees que sería un dato representativo?
   Nota que son los mismos precios a excepción de uno, ya que es un combo especial familiar que cuesta $120. Este es un dato atípico, es decir poco común o sobresaliente del conjunto de datos.
   
   Calcula la media, primero suma todos los datos del conjunto 34 + 40 +120 + 37 + 33 + 39 es igual a 303 Enseguida divide entre 6, que es el número de postres disponibles. El resultado es 50.5. Como te das cuenta la media aritmética cambió de 35.50 pesos a 50.5 pesos, aumentó 15 pesos
   ¿Consideras que este nuevo valor es representativo de todos los precios de los postres disponibles en la cafetería?
   Se considera que no es un valor representativo, porque cinco de los seis precios están muy por debajo del valor de la media, en el caso anterior, los datos eran mejor representados por el valor del promedio 35.5´.
   ¿Por qué pasa esto? ¿Qué debes hacer cuando esto sucede?
   Esto sucede porque la media aritmética es una medida sensible a los valores atípicos, es decir, aquellos que no son cercanos al resto de los datos del conjunto.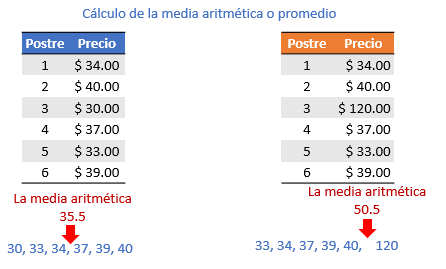
   
   Para el ejemplo, si ordenas los datos de ambos conjuntos de menor a mayor o si los representaras en una recta numérica, puedes ver que la media está al centro del conjunto de datos, es decir, la mayoría rondan los 35.5 pesos, caso contrario al segundo conjunto, ya que la media es mucho mayor que la mayoría de datos, debido al postre de 120 pesos, este dato afecta el valor de la media.
   Para saber qué tan diferente es el valor de la media aritmética o promedio con respecto a los datos del conjunto se utilizan las medidas de dispersión. En específico centrarás el estudio en el Rango. Presta atención al siguiente audiovisual.
   Observa del minuto 00:34 al 01:05.
2. Relación entre el rango y la posible dispersión de los datos.
   https://youtu.be/gcw4dPYoH08
   Como te diste cuenta el rango, es una medida de dispersión y se obtiene restando el dato mayor menos el dato menor del conjunto.
   
   Esta diferencia permite conocer que tan alejados o dispersos están el dato mayor y el dato menor.
   Cuando estás muy disperso el uno del otro, es decir, cuando el rango es grande, el valor de la media se verá afectado y estará lejos de representar apropiadamente a todo el conjunto.
   
   Por el contrario, si la diferencia o la dispersión entre el dato mayor y el dato menor es pequeña, es decir, cuando el rango es un valor reducido, entonces, la media aritmética es adecuado para representar al conjunto de datos.
   
   Retoma el ejemplo del segundo conjunto de postres y calcula el rango, los datos del conjunto son los precios de los postres son:
   34, 40, 120, 37, 33 y 39.
   Primero identificas el dato mayor, que es 120, ahora observa que el dato menor es 33. Para calcular el rango restas 120 menos 33 que resulta 87. El rango de este ejemplo es 87.
   ¿Qué te hace saber este valor del rango?
   Parece que es un valor elevado, en comparación con los otros valores, porque la mayoría de los precios de los postres oscilan entre los 30 y 40 pesos. Esto comprueba que cuando el rango es grande, los datos extremos están alejados y por consiguiente el promedio está lejos de representar al conjunto.
   ¿Cuál sería el valor del rango para ese conjunto de datos?
   
   Para calcular el rango solamente es necesario restar al valor del extremo superior el valor del extremo inferior. De manera que 40 menos 33 resulta ser 7. El rango de este ejemplo es 7.
   Es muy evidente que, en comparación con los precios de los postres, 7 es un valor pequeño. Así que la media de 35.5 que calculaste para estos datos sí es representativa del conjunto.
   Ya observaste cómo un valor atípico afecta la representatividad de la media aritmética de un conjunto de datos. Observa una segunda posible situación ¿Qué sucedería con el valor de la media y el rango cuando hay datos que se repiten?
   Si todos los datos se repitieran, es decir si todos fueran los mismos entonces el valor de la media sería ese valor repetido. Como cuando todos los alumnos sacan puro 10 en sus asignaturas, entonces su promedio es 10. En ese caso, el valor del rango sería cero, dado que todos los datos son iguales y la diferencia entre ellos es nula. Es el mínimo valor que el rango puede tener.
   Si el rango es cero, la media aritmética representa perfectamente al conjunto de datos, porque en realidad la medía sería exactamente igual al valor que se repite.
   Si hay valores que se repiten en un conjunto de datos, esto ayuda a reducir el valor del rango y por lo tanto a que la media aritmética sea más representativa del conjunto. Sin embargo, si hay valores atípicos, estos harán que el rango se amplíe haciendo que la media o promedio sea menos representativa de los datos. Entonces es mejor buscar otra medida de tendencia central para representar al conjunto. Por ejemplo, la moda o la mediana.
   Observa algunos ejemplos de esta situación.
   Observa del minuto 03:26 al 05:20.
3. ¿Cómo cambia la media aritmética?
   https://youtu.be/sLEu_Cv2fCM
   Para tener mayor claridad de que la media no es representativa realiza un análisis más profundo.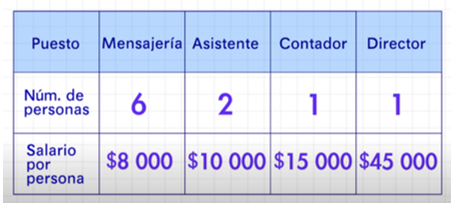
   
   En el ejemplo hay valores que se repiten y también hay al menos un valor atípico. Observa la tabla. El dato 8 000 se repite 6 veces. Además, hay un valor que es casi el doble de 8 000, el sueldo del contador es de $15 000, así que un dato atípico es 15000.
   Sin embargo, hay un valor aún más extremo: 45000, ¿Cuál es el rango de este conjunto de datos?
   
   El rango se calcula obteniendo la diferencia de los datos extremos, en este caso esos datos son 45 000 y 8 000. Si a 45 000 le resto 8 000, entonces obtengo 37 000. El rango es 37 000, que es un valor muy grande comparado con los 8 000 que es el dato que más se repite.
   A partir del rango es muy evidente que la media 12 800 no es representativa del conjunto, cuando la mayoría de trabajadores gana menos de esa cantidad.
   Así que es necesario usar otra medida de tendencia central para representar al conjunto como pudiste observar la mediana es 8000, Este valor representa mejor a la mayoría de los datos del conjunto.
   En este caso la media no es una media de tendencia central útil es mejor la mediana para estas situaciones. ¿Qué hay de la moda?
   La mediana es menos susceptible a los valores atípicos, la moda también. Presta atención del minuto 05:21 al 05 56.
4. ¿Cómo cambia la media aritmética?
   https://youtu.be/sLEu_Cv2fCM
   Para concluir con la lección observa el último ejemplo que resume todo lo que has aprendido hoy. Presta atención del minuto 01:44 al 03:08.
5. Relación entre el rango y la posible dispersión de los datos.

https://youtu.be/gcw4dPYoH08

El reto de hoy:

Puedes solicitar a tus maestras o maestros a distancia que te pongan más ejercicios de este tipo.

Puedes consultar tus notas o pedir retroalimentación a tus maestras o maestros sobre este tema cuando lo necesites.

Además, si ya tienes tu libro de Matemáticas de primer grado, ubica en él este tema. Resuelve todo lo que puedas para practicar. Tal vez encuentres formas diferentes para realizar estos cálculos. Anota tus dudas y no te pierdas la siguiente lección.

También puedes pedir ayuda, y retroalimentación a distancia, de tus maestras o maestros; cuando sea posible.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/