Porcentajes y gráficas circulares
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06Aprendizaje esperado: recolecta, registra y lee datos en gráficas circulares.
Énfasis: construir gráficas circulares a partir del establecimiento de porcentajes.
¿Qué vamos a aprender?
En esta sesión construirás gráficas circulares a partir de establecer porcentajes.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, sacapuntas y tu juego geométrico. Así como tu libro de texto de la asignatura.
En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué hacemos?
Para iniciar este tema, se te recuerda que debes respetar todos los protocolos sanitarios establecidos, así como cuidar tu alimentación para mantener una buena salud.
Por ejemplo, Lulú una compañera tuya, dice que siempre que va a preparar su comida recuerda “El plato del bien comer”, pero cree que se está alejando del tema.
Pero, al contrario, si te fijas la imagen del plato del bien comer que menciona Lulú representa una gráfica circular, que tiene que ver con el tema de estudio de esta sesión. En él se presentan cada uno de los tres grupos de alimentos que son: Verduras y frutas, cereales y leguminosas y alimentos de origen animal. Está diseñado con el objetivo de tener una alimentación balanceada.

Para conocer más sobre las gráficas circulares, es necesario que se establezcan algunos conceptos importantes.
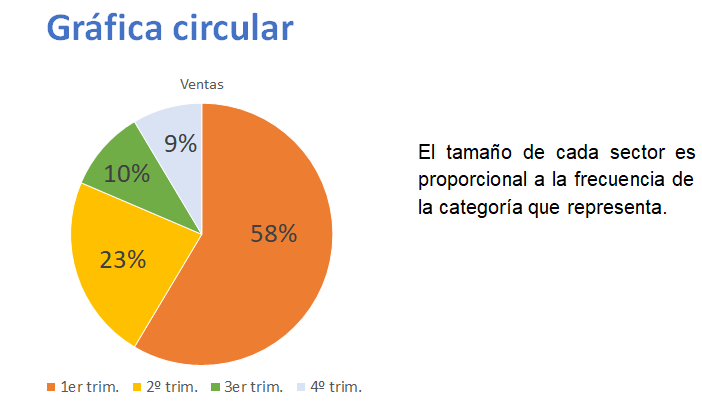
Como has visto antes, una gráfica circular consta de un círculo dividido en sectores que corresponden a categorías de datos. El tamaño de cada sector es proporcional a la frecuencia de la categoría que representa.
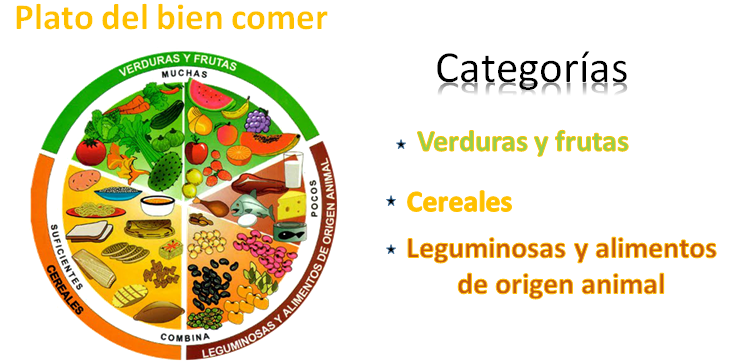
Asociando lo que acaba de mencionar, con el plato del bien comer, se puede asegurar que las categorías son:
- Verduras y frutas.
- Cereales.
- Leguminosas y alimentos de origen animal.
Pero ¿qué son los sectores?
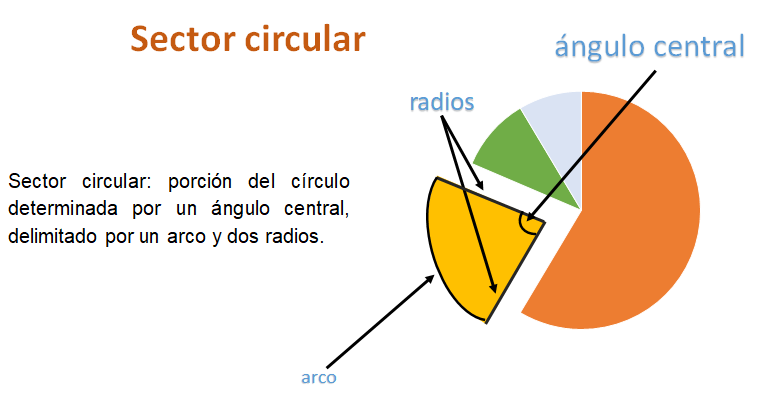
Se denomina sector circular a la porción del círculo determinada por un ángulo central formado por dos radios; quedando así delimitado por un arco y dos radios.
En el plato del bien comer puedes observar tres sectores: el color verde que corresponde a verduras y frutas, el amarillo que corresponde a cereales y el naranja que representa a las leguminosas y alimentos de origen animal.
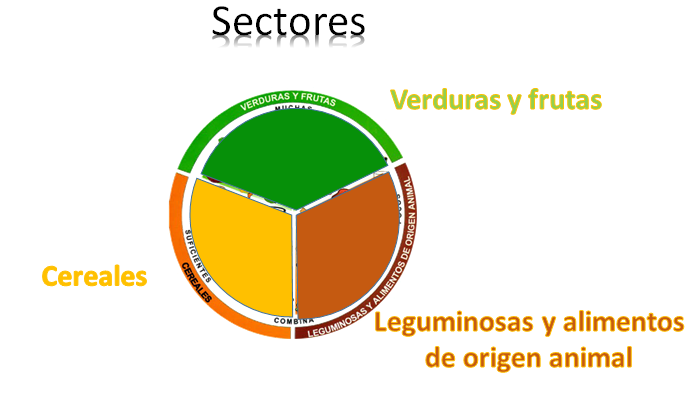
Es importante mencionar que la medida de cada sector circular, está dada por el tamaño del ángulo central, es decir, la unidad de medida de un sector circular son los grados. Un círculo o una vuelta completa comprende 360 grados, en este caso los tres sectores son exactamente iguales por lo que se puede calcular la medida de cada uno de ellos dividiendo 360 entre 3 que es igual a 120. Con esto se puede afirmar que cada sector circular mide 120º grados.
Se entiende entonces que una dieta balanceada debe incluir, verduras y frutas, cereales y leguminosas y alimentos de origen animal. Como los tres grupos corresponden al 100 por ciento, cada categoría sería del 33.3%.
Con este ejemplo, se puede observar que la gráfica circular también llamada gráfica de sectores o gráfica de pastel, tiene como objetivo representar variables cualitativas o categóricas. Se utiliza para mostrar las proporciones por medio de porcentajes, además permite representar la importancia relativa de un dato, respecto al todo. Se recomienda utilizarla cuando las categorías son pocas, ya que, si el grafico tiene muchas variables casi no aporta información y sería incomprensible.
De todas las gráficas que existen, en las circulares se puede leer más fácilmente la información que en ellas se presenta, pero, quizás no recuerdes como se construyen. Así que hay que recordarlo.
Para ello, se resolverá la siguiente situación:
En el deportivo de una colonia se observa una tabla en la que se muestran el número de alumnos inscritos en cada uno de los deportes que ahí se practican.
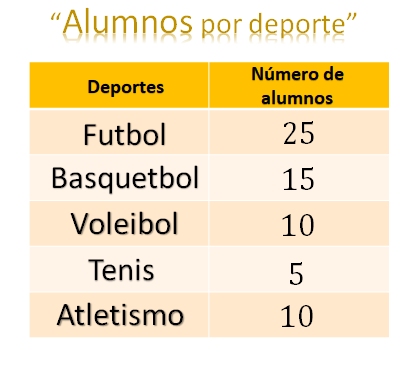
En la primera columna están los deportes que son: futbol, basquetbol, voleibol, tenis y atletismo y en la segunda el número de alumnos: 25, 15, 10, 5 y 10, respectivamente.
¿Qué se te ocurre que se debe hacer primero?
Como en la gráfica circular se representan las partes de un todo, lo primero que se debe hacer es calcular el total de alumnos inscritos ya que eso será el total.
Así que, hay que calcular el total y hay que aprovechar para agregar tres columnas a la tabla y colocar en ellas la frecuencia relativa, el porcentaje y la medida del ángulo central del sector que corresponderá a cada deporte, que serán necesarios para trazar y representar los datos de la gráfica.
Correcto, si te es posible, copia la tabla en tu cuaderno y si tienes a la mano un juego de geometría, traza la gráfica circular.
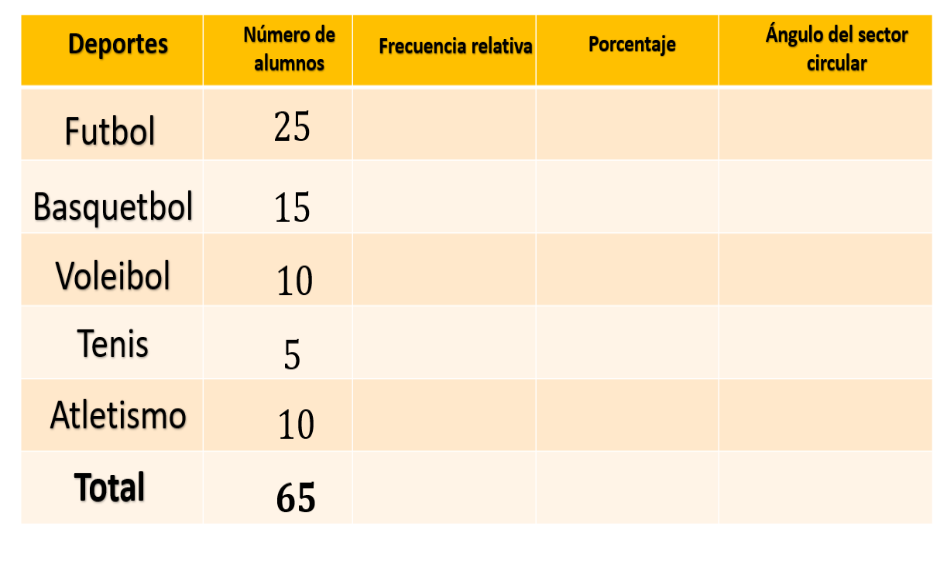
Agrega una fila en donde colocarás el total, que resulta de sumar 25 más 15, más 10, más 5, más 10 igual a 65. Agregas una columna para la frecuencia relativa, una para porcentaje y una más para la medida del sector circular.
Ahora, hay que calcular las frecuencias relativas. Recuerda que la frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos. En este caso las frecuencias absolutas son el número de alumnos entre el total de datos, que son 65.
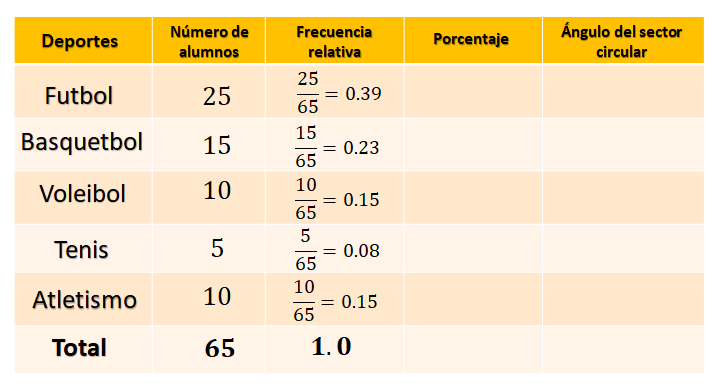
Para calcular las frecuencias relativas se debe dividir el número de alumnos de cada deporte entre el total de alumnos y redondear el resultado a centésimos.
Cabe aclarar que, al redondear los resultados, las diferencias con el valor real serán mínimas por lo que los sectores circulares, en la construcción de la gráfica, no se verán afectados, en cuanto a su tamaño y proporción.
Para el futbol se divide 25 entre 65, y se obtiene treinta y nueve centésimos; para el basquetbol se divide 15 entre 65, igual a veintitrés centésimos; para el voleibol se divide 10 entre 65, igual a quince centésimos; para el tenis se divide 5 entre 65, igual a ocho centésimos y para atletismo se divide 10 entre 65, igual a quince centésimos.
Al sumar las frecuencias relativas se obtiene un entero.
El cálculo de las frecuencias relativas te ayudará a obtener los porcentajes de una manera muy práctica, solo debes multiplicar la frecuencia relativa por 100. Este dato te será de utilidad para la representación de las categorías en la gráfica circular.
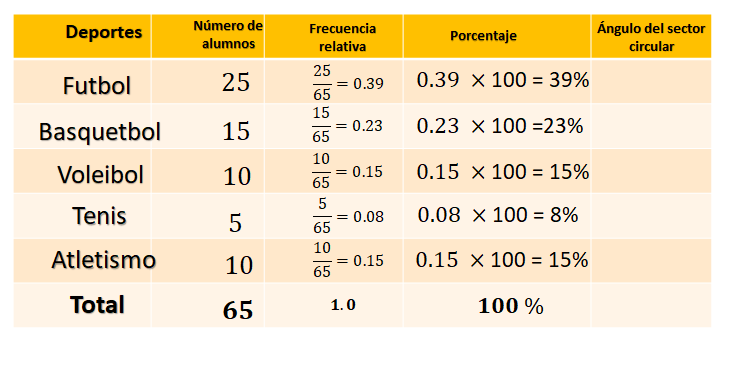
Para futbol, treinta y nueve centésimos por 100, igual a 39%; basquetbol, veintitrés centésimos por 100, igual a 23%; voleibol, quince centésimos por 100, igual a 15%; tenis, ocho centésimos por 100, igual a 8% y para atletismo, quince centésimos por 100, igual a 15%. Al sumar los porcentajes se obtiene el 100%.
Ya que conoces la frecuencia relativa y el porcentaje, sólo te falta calcular el ángulo del sector circular. Y según lo que se te ha explicado, la proporción que representa cada categoría respecto al total, debe guardar la misma proporción que el sector circular que le corresponde respecto al círculo completo.
Así es, al total de datos le corresponde el área que abarca los 360º, es decir, 100% de los datos. El ángulo que corresponde a cada categoría debe cumplir con la proporción.
Categoría entre total, igual a sector circular entre 360º, y también pueden obtenerse usando los porcentajes; porcentaje de la categoría entre 100% es igual a sector circular entre 360º.
Por lo tanto, el ángulo para cada categoría está dado por:
Sector circular igual a categoría entre total por 360º o también, porcentaje de la categoría entre 100% por 360º.
Pero, categoría entre total, es lo que ya se calculó en la frecuencia relativa. ¿Cierto?
Así es. Es importante saberlo, aunque podrías usar los porcentajes, lo que se comenta te permite hacer el cálculo aún más rápido; esta es otra ventaja de haber calculado la frecuencia relativa. Ahora, hay que regresar a la tabla para completar la última columna.
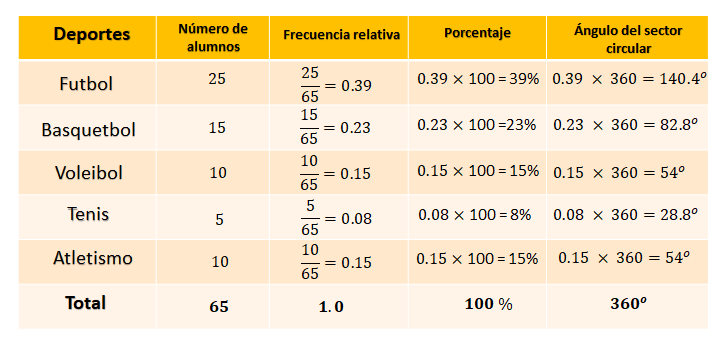
Para futbol, treinta y nueve centésimos por 360, igual a 140.4º; basquetbol, veintitrés centésimos por 360, igual a 82.8º; voleibol, quince centésimos por 360, igual a 54º; tenis, ocho centésimos por 360, igual a 28.8º y para atletismo, quince centésimos por 360, igual a 54º. Al sumar las medidas de los ángulos se obtiene 360º.
Ya tienes todos los datos, ahora hay que construir la gráfica.
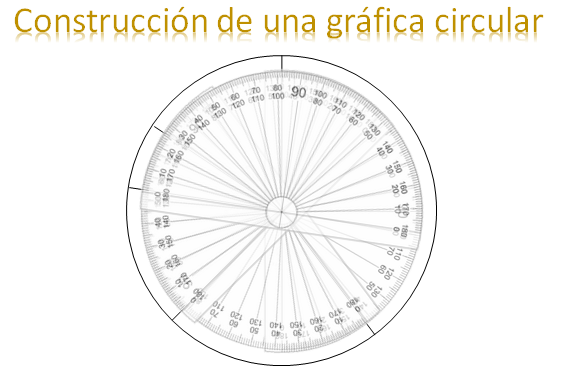
Primero debes trazar una circunferencia, la medida es indistinta; ubica el centro del circulo y traza un radio del círculo, generalmente se inicia de esta forma para seguir el sentido de las manecillas del reloj, con el transportador marcas el primer ángulo que es de 140.4º.
Colocas el transportador en el centro del círculo, pero ahora te apoyas en la marca anterior y ubicas la medida del segundo ángulo que es de 82.8º. Vuelves a colocar el transportador en el centro, te apoyas en la marca anterior y mides el tercer ángulo que es de 54º.
Nuevamente ubicas el transportador en el centro del circulo y marcas el cuarto ángulo cuya medida es de 28.8º y si los trazos fueron correctos automáticamente te queda el último sector circular cuyo ángulo mide 54º.
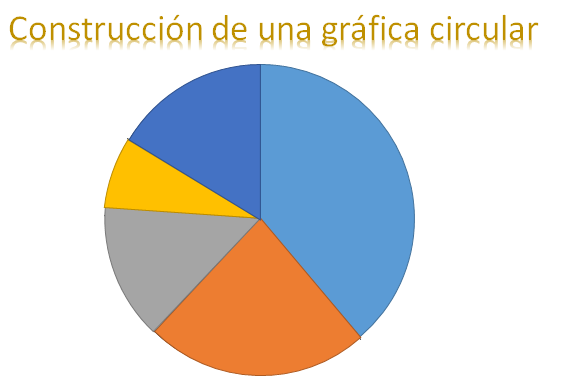
Ahora sólo tienes que colorear cada sector circular, pon de azul el que corresponde a futbol; de naranja, al basquetbol; de gris voleibol, de amarillo tenis y de azul marino atletismo.
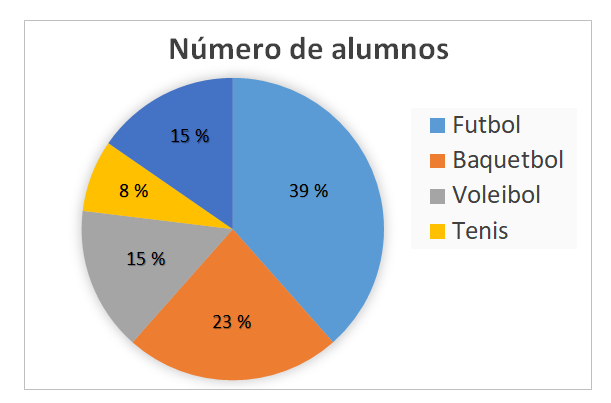
Ahora coloca en tu gráfica los porcentajes que corresponden a cada categoría, futbol 39%, basquetbol 23%, voleibol 15%, tenis 8% y atletismo 15% y en un lado pondrás el nombre de las categorías con el color asociado a cada una de ellas, para que la lectura de la gráfica sea más sencilla. Y así tengas completa tu gráfica y puedas analizar la información de manera sencilla.
Regresando al tema de alimentación, hay una tabla que se considera que, si la información hubiera estado presentada en una gráfica circular, la información sería aún más significativa.
Hay que realizarla.
Primero se revisará cuál era la situación. De ser posible escribe en tu cuaderno y ve resolviendo.

El título es “Alimentos en los que más gasta el mexicano” y dice que se han encuestado a 1000 personas y los resultados están presentados en una tabla, en la primera columna los alimentos: Carne, frutas y verduras, cereales y leguminosas; en la segunda columna los porcentajes: 40.3%, 27.5%, 20.7% y 11.5% respectivamente.
Con los datos dados como porcentajes, ya se puede trabajar en la construcción de la gráfica circular, pero para seguir el proceso anterior y que tengas toda la información, realiza lo siguiente.
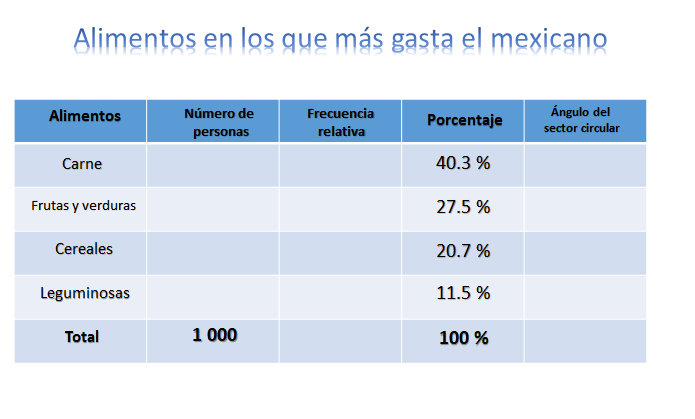
Lo primero que harás es agregar las columnas a la tabla, ya que sabes que necesitas calcular, el número de personas por cada tipo de alimento, la frecuencia relativa y la medida del ángulo del sector circular, el cual será necesario para trazar la gráfica.
También agregarás una fila en donde colocarás el total, en este caso el único que conoces es el total de personas encuestadas que fueron 1000 y el de porcentaje que resulta de sumar 40.3%, más 27.5%, más 20.7%, más 11.5%, que te da un total de 100%. Después se calcula el número de personas para cada categoría, como el total de personas encuestadas fue 1000, se multiplica el porcentaje por 10, o aún más práctico sólo se recorre el punto decimal una cifra a la derecha.
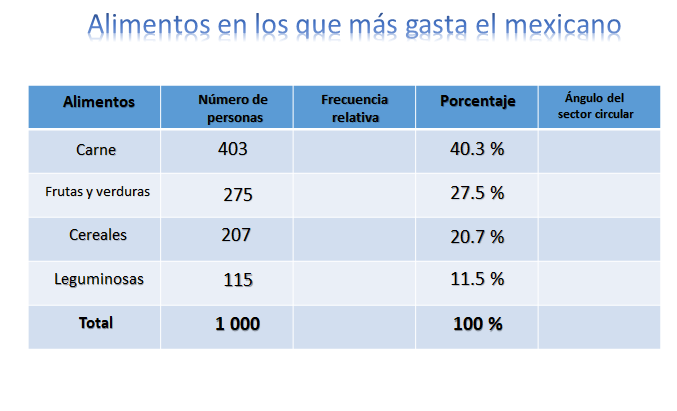
Para carne 40.3 por 10, 403; 27.5 por 10, 275; 20.7 por 10, 207; 11.5 por 10, 115. Y se comprueba que la suma, 403 más 275, más 207, más 115 es igual a 1 000.
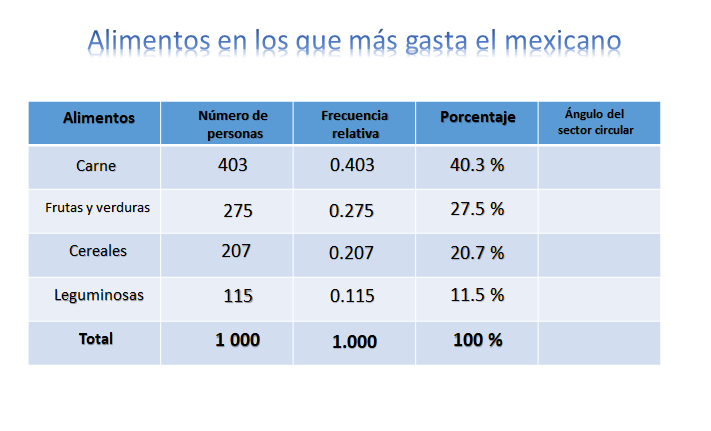
Ahora, debes calcular la frecuencia relativa. Como viste antes, se divide el número de personas de cada categoría entre el total, pero cómo estás trabajando con potencias de 10, en este caso 1000, entonces solo se recorre el punto tres lugares a la izquierda quedando: Carne 403 milésimos, frutas y verduras 275 milésimos, cereales 207 milésimos, leguminosas 115 milésimos, obteniendo un total de un entero.
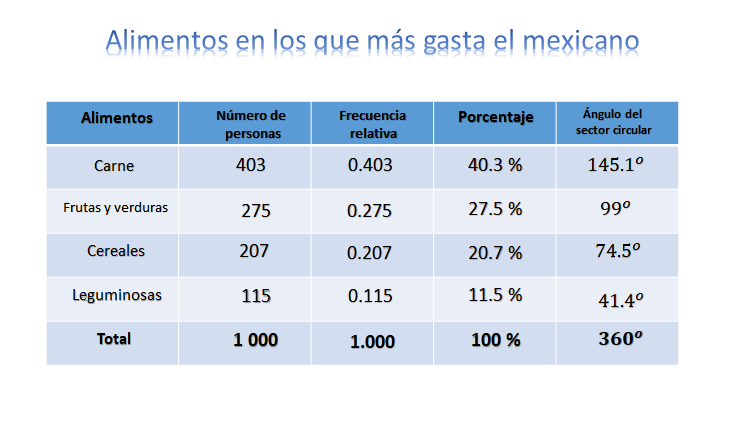
Ya que conoces la frecuencia relativa y el porcentaje, solo te falta calcular el ángulo del sector circular y si recuerdas, solo es multiplicar la frecuencia relativa por 360º.
Para la carne es 403 milésimos por 360 es igual a 145.1º; para frutas y verduras, 275 milésimos por 360 es igual a 99º; para la categoría cereales, 207 milésimos por 360 igual a 74.5º; leguminosas 115 milésimos por 360 igual a 41.4º, obteniendo un total de 360º.
Ya tienes todos los datos, ahora es momento de trazar la gráfica.
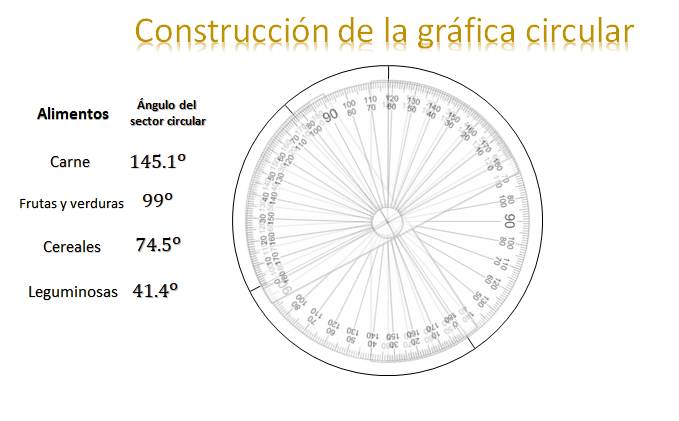
Primero trazas la circunferencia de cualquier medida; ubicas el centro del circulo y trazas el radio del circulo; con el transportador marcas el primer ángulo que es de 145.1º.
Mueves el trasportador tomando como base el ángulo que ya marcaste, sin perder el centro del círculo y marcas el segundo ángulo que es de 99º, vuelves a hacer lo mismo, pero marcas 74.5º, y si el procedimiento fue correcto te queda el ultimo ángulo de 41.4º.
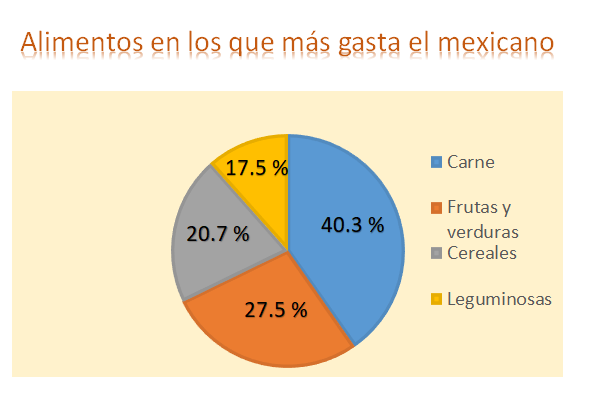
Ahora colocarás los porcentajes que corresponden a cada categoría, carne que le corresponde 40.3% de las personas; frutas y verduras, 27.5%, cereales 20.7% y leguminosas 11.5% y colocas las categorías asociadas al color que las representa.
En efecto, la información luce mucho mejor en una gráfica, que sólo ver su contenido en una tabla. Y ahora que ves la gráfica ya terminada, y que sabes que se ocuparon muchos cálculos para realizarla. Piensa, ¿se podría llenar una tabla como la que se complementó?
Así es, lo único que tendrías que conocer aparte de la gráfica, es el total de datos.
Presta atención a lo siguiente:
Hace unos meses una maestra les pidió a sus alumnos que hicieran una gráfica circular en donde registraran las actividades que realizan en un día.
Una de las alumnas le envió la siguiente gráfica.
Analiza la gráfica y responde la siguiente pregunta:
¿Qué datos observas en ella?
Escribe en tu cuaderno tus observaciones.
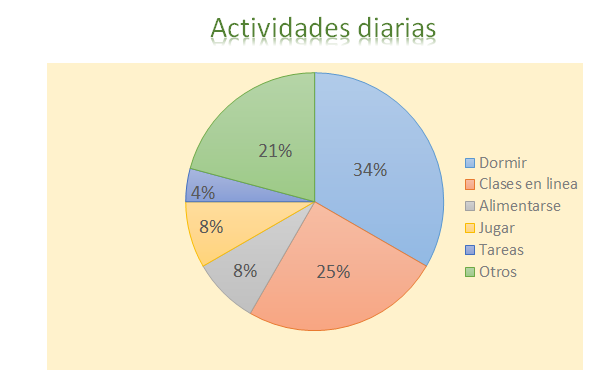
Puedes notar que las categorías son: Dormir, clases en línea, alimentarse, jugar, tareas y otros y tienen el 34%, 25%, 8%, 8%, 4%, y 21% respectivamente. Además, sabes que el total debe ser 24 ya que la gráfica se refiere a las actividades diarias y un día tiene 24 horas.
Perfecto, se espera que hayas tenido las mismas observaciones.
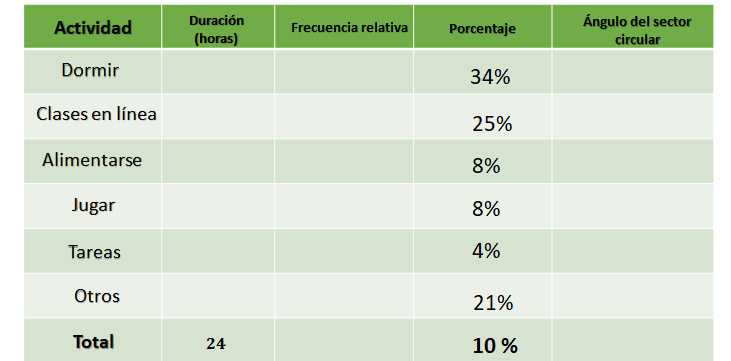
Ahora, organiza los datos conocidos en una tabla, para calcular todos los datos que involucra la gráfica. En la primera columna colocas las categorías que en este caso corresponden a la actividad: dormir, clases en línea, alimentarse, jugar, tareas, otros y total que también sabes que es de 24. En la columna de porcentaje escribes 34%, 25%, 8%, 8%, 4%, 21% y el total que es 100%.
Para calcular la frecuencia relativa debes hacer lo contrario, es decir, en lugar de multiplicar la frecuencia relativa por 100, debes dividir el porcentaje entre 100. Y al tratarse de esta cantidad lo único que debes hacer es recorrer el punto dos lugares a la izquierda, y eso puedes hacerlo mentalmente.
Hay que completar la columna correspondiente en la tabla de datos.
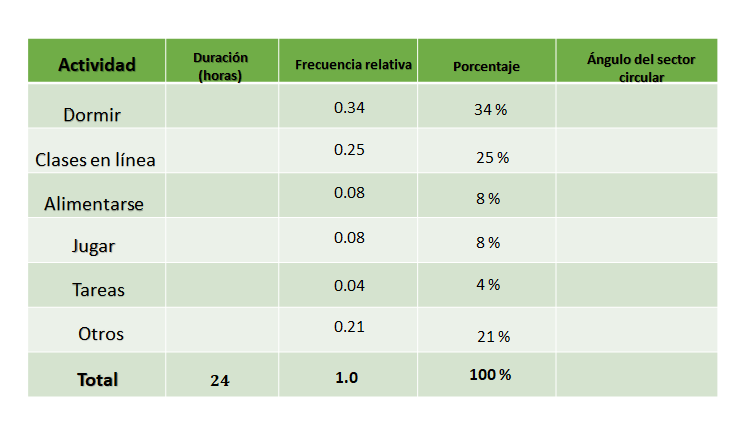
34% entre 100 es igual a treinta y cuatro centésimos, 25% entre 100 es igual a veinticinco centésimos, 8% entre 100 es igual a ocho centésimos, nuevamente 8% entre 100 es igual a ocho centésimos, 4% entre 100 es igual a cuatro centésimos y 21% entre 100 es igual a veintiún centésimos; lo que te da un total de un entero.
Es importante aclarar que la frecuencia relativa que se calculó, es el cociente entre la frecuencia absoluta de cada actividad entre el número total de datos y para saber las horas de cada categoría tienes la relación: categoría entre total igual a frecuencia relativa.
Por lo tanto, la frecuencia relativa para cada categoría está dada por: Categoría igual a frecuencia relativa por total, que es lo mismo que calcular los porcentajes dados de 24 horas, ya que la frecuencia relativa, también representa al porcentaje como número decimal.
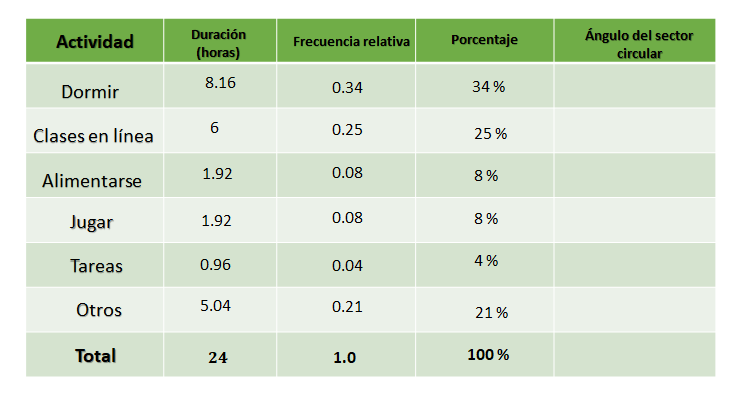
Treinta y cuatro centésimos por 24 es igual a 8.16 horas, veinticinco centésimos por 24 es igual a 6 horas, ocho centésimos, por 24 es igual a 1.92 horas, que se repite en jugar; 1.92 horas, cuatro centésimos por 24 es igual a 0.96 horas y veintiún centésimos por 24 es igual a 5.04 horas; lo que te da un total de 24, que corresponde a las horas de un día.
Calcula ahora la medida del ángulo del sector circular, multiplicando la frecuencia relativa por 360, que como se dijo antes, es lo mismo que calcular los respectivos porcentajes de 360.
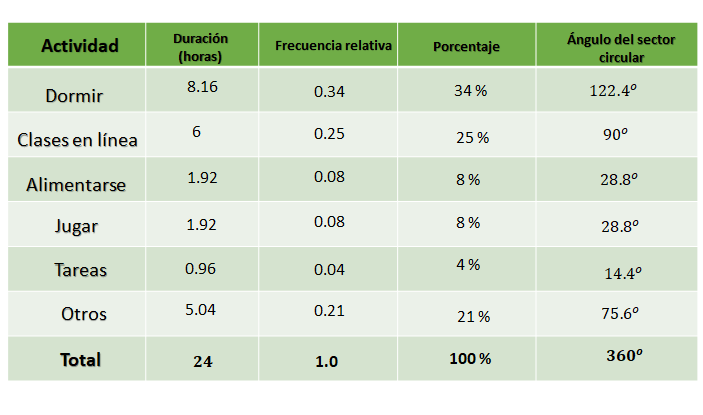
Treinta y cuatro centésimos por 360 es igual a 122.4º, veinticinco centésimos por 360 es igual a 90º, ocho centésimos, por 360 es igual a 28.8º dato que se repite en la siguiente fila; 28.8º, cuatro centésimos por 360 es igual a 14.4º y veintiún centésimos por 360 es igual a 75.6º; lo que te da un total de un 360º.
Se espera que esta explicación, sea de utilidad cuando requieras un dato más especifico en una gráfica circular.
El reto de hoy:
Si te es posible contacta con tu profesora o profesor para compartir tus respuestas. Por otra parte, revisa tu libro de texto y ubica el aprendizaje esperado de esta sesión, con la finalidad de que resuelvas todo lo que puedas y profundices más en este tema.
Asimismo, concluye tus ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion