Fiesta con frutas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Aprendizaje esperado: Resolución de problemas que impliquen particiones en tercios, quintos y sextos. Análisis de escrituras aditivas equivalentes y de fracciones mayores o menores que la unidad.
Énfasis: Resolver problemas de reparto que implican usar y comparar fracciones (medios, cuartos, octavos; tercios, sextos; quintos, décimos).
¿Qué vamos a aprender?
Seguirás aprendido sobre la representación gráfica de las fracciones.
La sesión anterior viste cuál es la estructura de las fracciones, lo que es una fracción equivalente, mayor o menor, y has aprendido a leerlas correctamente. También empezaste a resolver algunas situaciones de reparto a través de la representación gráfica de las fracciones. Hoy continuarás estudiando este tema.
Para empezar y recordar lo que ya has aprendido, contesta las siguientes preguntas:
¿Qué fracciones se representa en la siguiente imagen, y cuál es mayor?

Resuelve y contesta en tu cuaderno.
Comprueba tu respuesta con la imagen que se presenta a continuación.
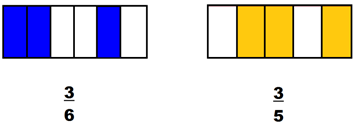
Realizando la comparación de fracciones, se obtiene que
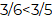 lo cual se lee “tres sextos es menor que tres quintos”.
lo cual se lee “tres sextos es menor que tres quintos”.
Recuerda que entre más grande es el denominador, más chica es la fracción.
En este caso, tienen el mismo numerador (3) pero denominadores diferentes, y 6 es mayor que 5, por lo tanto 3/6 es menor que 3/5
Observa ahora la siguiente imagen que presenta un entero dividido en ocho partes iguales, es decir en octavos.
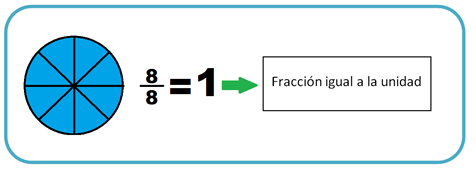
Las fracciones que representan un entero, se caracterizan por tener el numerador y el denominador iguales.
Esta actividad que acabas de realizar, te permitirá continuar con el trabajo de la sesión del día de hoy.
Si tienes libros en casa o cuentas con Internet, explóralos para saber más.
¿Qué hacemos?
Lee con atención la siguiente explicación sobre las fracciones impropias.
Se llaman fracciones impropias a las que representan números mayores que la unidad .
Todas las fracciones que representan un número mayor que la unidad se caracterizan por tener el numerador mayor que el denominador, a éstas se le conoce como “fracción impropia”.
Observa los siguientes ejemplos:

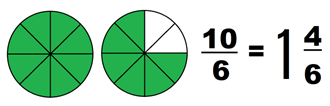
Resuelve el desafío número 7 Fiesta y pizzas , de la página 20 de tu libro.
https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/20
Lee con atención el siguiente planteamiento:
Al terminar el torneo de voleibol, algunos jugadores celebraron con una fiesta. Los asistentes se organizaron en pequeños grupos de distinta cantidad de integrantes para comprar frutas, si las frutas se repartieron en partes iguales en el interior de cada grupo, ¿Qué porción le tocó a cada integrante de cada grupo?
Trata de resolver el problema por ti mismo, después compara tus respuestas con la siguiente explicación.
Grupo 1. Se divide cada pizza en tres partes iguales y se reparte a cada persona dos de esas partes, de manera que a cada persona le tocó 1/3+ 1/3, o bien, 2/3
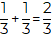
|
|
Situación |
Descripción de la situación. |
Parte de fracción de pizza que le toca a cada uno. |
|
Grupo 1 |
|
Repartir dos pizzas entre tres personas. |
Si se divide cada pizza en tres partes; a cada quien le toca 2/3 de pizza. |
Grupo 2. Se dividen las cuatro frutas en tercios y dar a cada persona 1/3 de cada pizza, así cada persona recibió 4/3 de pizza.
|
|
Situación |
Descripción de la situación. |
Parte de fracción de pizza que le toca a cada uno. |
|
Grupo 2 |
|
Repartir cuatro pizzas entre tres personas |
Si se divide cada pizza en tres partes; a cada quien le toca 4/3 de pizza, o
|
Si se unen 3/3 de los recibidos, se puede formar una pizza y queda una rebanada suelta, de manera que esta situación pude representarse a través de la siguiente escritura:

A cada niña o niño, le tocó más de una pizza.
Grupo 3. Se reparten tres frutas para cinco personas. Una forma de reparto, puede ser dividiendo cada pizza en cinco partes iguales y repartir a cada persona tres de ellas, es decir, 3/5
|
|
Situación |
Descripción de la situación. |
Parte de fracción de pizza que le toca a cada uno. |
|
Grupo 3 |
|
Repartir tres pizzas entre cinco personas. |
Se divide cada pizza en cinco partes; a cada quien le toca 3/5 de pizza. |
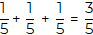
Grupo 4. Se reparten tres frutas entre cuatro personas. Una forma de reparto puede ser, dividiendo cada pizza en cuatro partes, por lo que a cada persona le tocó 3/4
|
|
Situación
|
Descripción de la situación. |
Parte de fracción de pizza que le toca a cada uno. |
|
Grupo 4 |
|
Repartir tres pizzas entre cuatro personas. |
Se divide cada pizza en cuatro partes; a cada quien le toca 3/4 de pizza. |

Otra forma de expresar lo que le tocó a cada quien en el grupo 4 recordando que 1/2 es equivalente a 2/4 sería: A cada quien le tocó 12+14 de pizza.

Ahora contesta la siguiente pregunta:
¿A qué grupo le tocó más de una pizza? considerando que:
- En el grupo 1 le tocó a cada integrante 2/3
- En el grupo 2 le tocó a cada integrante 113
- En el grupo 3 le tocó a cada integrante 3/5
- En el grupo 4 le tocó a cada integrante 3/4
Analizando y comparando las fracciones, le tocó más pizza al grupo 2 porque si se juntan 3 rebanadas se puede formar una pizza completa, ya que 3/3 = 1 y todavía queda una rebanada suelta, o sea que les tocó más de una pizza,
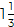
En el resto de los equipos la cantidad de pizza que les tocó es menos que una pizza entera o una unidad.
Resuelve el siguiente problema.
¿Cuántas pizzas se necesitan para que en un grupo de 6 personas a cada una le toquen 4/6 de pizza?
Una forma de resolverlo sería la siguiente:
Como son 6 personas, una pizza debe repartirse en 6 partes iguales, si repartimos esa primera pizza a cada quien le tocará 1/6 de la pizza y cómo queremos que cada quien al final del reparto tenga 4/6, entonces debemos repetir el proceso de repartir un sexto cuatro veces, por lo que entonces necesitamos cuatro frutas para que a cada quien le toque 4/6
Observa la siguiente imagen para comprender mejor la situación.
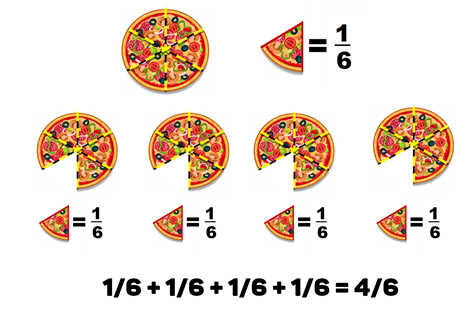
El Reto de Hoy:
Resuelve los siguientes problemas:
- Encuentra dos formas diferentes de repartir tres frutas, considerando dos números distintos de personas. Representa tanto el procedimiento de reparto como el resultado de la repartición.
- ¿Determina cuántas frutas y cuántas personas debe haber en una reunión para que a cada persona le toque 3/5 de una fruta?
Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
Descarga tu clase dando clic aqui
¡Buen trabajo!
Gracias por tu esfuerzo.








Login to join the discussion