Sucesiones Numéricas

Aprendizaje esperado: Identificación de la regularidad en sucesiones compuestas con progresión aritmética, para encontrar términos faltantes o averiguar si un término pertenece o no a la sucesión.

Énfasis: Reconocer la regla de variación en una sucesión compuesta formada por números, ya sea creciente o decreciente, e identificar los elementos faltantes o los siguientes.

¿Qué vamos a aprender?

En la sesión anterior estuviste trabajando con sucesiones compuestas de figuras y determinaste la regla de construcción y pudiste encontrar algunos elementos de esas sucesiones.

Aprenderás a reconocer la regla de variación en una sucesión compuesta formada por números, ya sea creciente o decreciente, e identificarás los elementos faltantes o los siguientes.

Para comenzar, conoce lo que es una sucesión de números:

Una sucesión o serie de números se forma a partir de un patrón o regla establecida. A este patrón se le conoce como regularidad o regla de variación.

Observa la siguiente sucesión de números:

A cada elemento de la sucesión se le conoce como término y es muy conveniente separar cada término de otro mediante una coma, y si requieres de mayor claridad en la escritura de los términos, considera además un espacio entre ellos.

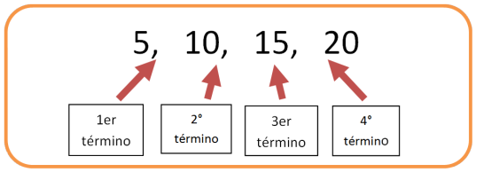
Resulta sencillo observar que esta sucesión va incrementando en cinco, por lo tanto, su regularidad indica que, para obtener el siguiente término, se suma 5 al anterior.

Se puede decir que es una serie numérica cuya regularidad es 5, ya que a cada número se le está sumando 5 ejemplo: 5+ 5=10, 10+5=15, 15+5=20, 20+5=25, etc.

Esto que acabas de analizar, te permitirá continuar con el trabajo de la sesión del día de hoy.

Si tienes libros en casa o cuentas con Internet, explóralos para saber más.

¿Qué hacemos?

Observa la siguiente serie de números:

15

30

45

75

90

¿Qué número falta en la casilla?

Analiza qué va sucediendo con las cantidades.

Como puedes ver, van aumentando. Cuando los términos de una sucesión van aumentando o siendo más grandes, entonces se dice que es una sucesión o progresión creciente .

¿Cuál es la operación que se debe aplicar al primer número para obtener el segundo? Seguramente ya te disté cuenta que se tiene que realizar una suma.

Al número 15 se le suma 15 para obtener como resultado 30, por eso la regularidad, patrón o regla de variación de esta progresión es:

“Sumar 15 al término actual para obtener el siguiente”

Observa que al escribir la regla de variación debes indicar qué operación debes aplicar para obtener el término que sigue. Puedes escribirla iniciando con mayúscula, entre comillas, con un color distinto, subrayándola, con mayúsculas todas las letras, etc., de manera que puedas identificarla fácilmente en tu cuaderno.

Si aplicas la regla de variación que acabas de redactar, entonces obtendrías los siguientes términos:

15+15=30

30+15=45

45+15=60

60+15=75

75+15=90

Si observas, una serie o progresión creciente utiliza la operación de sumar como medio para obtener los términos o elementos que la forman.

Arma una serie numérica que empiece con el número 12 y que vaya creciendo en +8, cada término.

Observa cómo se pude formar:

12+8=20

20+8=28

28+8=36

36+8=44

44+8=52

La sucesión quedaría así:

12

20

28

36

44

52

La regla de variación es:

“Sumar 8 al término anterior, para obtener el siguiente”

Analiza la siguiente sucesión numérica, ¿Cuál es su regularidad?

120

95

70

45

20

Analiza qué va sucediendo con las cantidades. Como puedes ver, se van reduciendo o disminuyendo.

Cuando los términos de una sucesión van reduciendo o disminuyendo o se vuelven más pequeños, entonces se dice que la sucesión o progresión es decreciente.

¿Cuál es la operación que se debe aplicar al primer número para obtener el segundo? Como se busca que el número siguiente sea menor, entonces se puede aplicar una resta.

Al número 120 se le resta 25 que da como resultado 95 y si a 95 le restas 25 obtienes 70

120 – 25 = 95

95 – 25 = 70

Verás que la regularidad o regla de variación de esta progresión es:

“Restar 25 al término actual para obtener el siguiente”

Para comprobar la regularidad aplica la regla de variación:

120 - 25=95

95 - 25=70

70 - 25=45=

45 - 25=20=

Observa la siguiente sucesión numérica.

23	28	33
1er término	2° término	3er término	4° término	5° término

Analiza qué va sucediendo con las cantidades. Como ves, van aumentando.

Recuerda que cuando los términos de una sucesión van aumentando o creciendo entonces se dice que la sucesión o progresión es creciente.

¿Cuál es la operación que se debe aplicar al primer número para obtener el segundo? Seguramente ya analizaste que como se busca que el número siguiente sea más grande, entonces se puede aplicar una suma: al número 23 se le suma 5 dando como resultado 28, y si a 28 se suma 5 obtienes 33

La regularidad o regla de variación de esta progresión es:

“Sumar 5 al término actual para obtener el siguiente”

Si observas, hay espacios vacíos en la serie, ¿Cuál será el número que ocupará el 5° término de esta sucesión? Para responder, primero debes conocer cuál es el 4º término.

¿Qué debes hacer para calcular el número que ocupa el 4° término? Se debe aplicar la regla o regularidad de variación que ya identificaste, en este caso es, sumar 5 al tercer término, por lo que:

33+5=38

Por lo tanto, el 4º término es 38

¿El número 49 es el que debe ir en la progresión como el quinto término? Para saberlo, tienes que sumar 5 al cuarto término que es 38 por lo que 38+5=43 así que definitivamente 49 no es el número que debe ir en el quinto término de la progresión, debe ser 43

Ahora contesta las siguientes preguntas: ¿El número 75 forma parte de esta progresión creciente? y si así fuera, ¿Qué lugar de la sucesión o progresión ocuparía?

Si recuerdas lo que has estudiado el día de hoy, puedes resolver estas preguntas.

¿Qué debes saber primero? Debes calcular los términos que faltan hasta ver si obtienes o no el 75 como parte de la serie, aplicando la regla de variación que es “sumar 5”

43+5=48

48+5=53

53+5=58

58+5=63

63+5=68

68+5=73

73+5=78

Como ves, con los números que has obtenido, ya pasaste el número 75 ya llegaste a 78 eso, ¿Qué indica?

Indica que 75 no es parte de la progresión, entonces ya tienes la primera respuesta. Falta saber qué lugar ocupa en la sucesión.

Pero como este término no es parte de la sucesión entonces no ocupa ningún lugar.

Contesta las siguientes preguntas: ¿El número 73 forma parte de esta progresión creciente? y si así fuera, ¿Qué lugar de la sucesión o progresión ocuparía?

Eso ya es fácil de saber porque el número 73 sí forma parte de la sucesión, ya lo puedes ver en los cálculos que hiciste, y al acomodar los términos puedes ver que ocupa el lugar 10 o también puedes decir que es el décimo término.

23	28	33	38	43
1er. término	2° término	3er. término	4° término	5° término

48	53	58	63	73
6° término	7° término	8° término	9° término	10° término

78
11° término	12° término	13° término	14° término	15° término

Observa con atención los números acomodados, ¿Qué observas? Tal vez puedes decir que están formados por dos cifras, pero también, el número final de cada término se repite, es decir, todos los términos tienen al final de forma alternada el número 3 como 23, 33, 43, etc. u otros terminan en 8 como 28, 38 y 48 esta es una característica de esta serie y te puede ayudar a responder, por ejemplo, si el número 85 es un término o no de esta serie. Con base en lo que ya observaste, entonces puedes decir que el 85 no forma parte de esta sucesión, porque termina en 5 y todos los números de esta progresión terminan en 3 o en 8

Compruébalo:

78+5=83

83+5=88

Como ves, el número 85 no forma parte de esta serie.

Es muy importante que observes con mucha atención las características de los números que van formando la progresión, ya que podrás obtener información muy importante.

Resuelve la siguiente situación:

En el cine los asientos están numerados. Jorge fue con sus papás a una función el fin de semana, sin embargo, no encontraron boletos para sentarse juntos; él y su mamá ocuparon el cuarto y el quinto asiento de una de las filas, asientos que tenían los números 10 y 14 respectivamente; su papá tuvo que sentarse ocho asientos más adelante:

¿Qué número tenía el asiento donde se sentó el papá de Jorge?

¿Qué lugar ocupó el papá de Jorge en la fila, si el asiento que tenía el número 10 era el cuarto asiento?

Para responder a la primera pregunta, debes iniciar tomando en cuenta el número del asiento donde se sentó la mamá de Jorge y él, para establecer cómo se va asignado el número a cada asiento, así tendrás los primeros dos números:

10, 14

Para conocer el número que tenía el asiento donde se sentó el papá de Jorge necesitas calcular el número de cada uno de los 8 asientos restantes.

¿Cuál será la regla de variación? Para responder, observa si la progresión es creciente o decreciente. Como ves, es creciente y la regla sería:

“Sumar 4 al término actual para obtener el siguiente”

Si aplicas la regla tienes lo siguiente:

10 + 4 = 14

14 + 4 = 18

18 + 4 = 22

22 + 4 = 26

26 + 4 = 30

30 + 4 = 34

34 + 4 = 38

38 + 4 = 42

42 + 4 = 46

Escribiendo esta progresión para los siguientes 8 términos, tendrás:

10,  14,  18,  22,  26,  30,  34,  38,  42,  46

Y, por tanto:

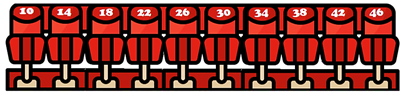
Ahora ya puedes responder las preguntas.

¿Qué número tenía el asiento donde se sentó el papá de Jorge? La respuesta sería: El asiento tendría el número 46

¿Qué lugar ocupó el papá de Jorge en la fila, si el asiento que tenía el número 10 era el cuarto asiento? La respuesta sería: El papá de Jorge ocupó el lugar 13

El Reto de Hoy:

Realiza la siguiente actividad.

Diseña una progresión simple, con el número de términos que quieras. Comienza redactando la regularidad.

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.