Ordenando las partes decimales

Aprendizaje esperado: Resolución de sumas o restas de números decimales en el contexto del dinero. Análisis de expresiones equivalentes.

Énfasis: Resolver problemas que impliquen sumar números decimales, en contextos de dinero, utilizando diferentes procedimientos, entre ellos el algoritmo usual o convencional.

¿Qué vamos a aprender?

Seguirás trabajando con problemas matemáticos que impliquen el uso de cantidades con punto decimal.

¿Qué hacemos?

Para comenzar, lee la siguiente nota sobre la palabra decimal:

Ahora analiza y resuelve el siguiente problema:

En la juguería “La Sana Distancia”, se ofrecen los siguientes alimentos en su menú.

Pedro fue a comprar un jugo de $ 12.40 y un sándwich de $ 18.65 ¿Cuánto pago en total?

Para resolverlo debes realizar una suma:

12.40 + 18.65 = 31.05

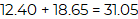
Puedes sumar primero los números enteros:

12 + 18 = 30

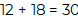
y después sumar la parte decimal:

40₵ + 65₵ = 105₵

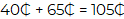
Dando como resultado 30 pesos con 105 centavos.

Los 105 centavos los debes convertir a pesos, considerando que en un peso hay 100 centavos. Por lo que el resultado es 1 peso con 5 centavos.

$ 30.00 + $ 1.05 = $ 31.05

También puedes encontrar el resultado utilizando el procedimiento que ya conoces de la suma. Recuerda que el punto decimal de las cantidades sirve como referente para acomodar alineados todos los sumandos:

Resolviendo la operación:

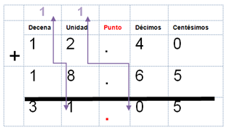
Es muy importante recordar que, al finalizar la realización de la operación, debes colocar el punto decimal justo bajo la posición que sirvió de referente para alinear todos los sumandos.

En este resultado en particular, es fácil convertir centavos a pesos, recordando que 100 centavos son un peso, por ejemplo:

Esta actividad que acabas de realizar te permitirá seguir aprendiendo sobre este tema.

Si tienes libros en casa o cuentas con Internet, explóralos para saber más.

Analiza y resuelve el siguiente problema.

La mamá de Carlos fue al mercado y compró 2 kg de manzanas a $12.50 el kg, 1 kg de mangos a $38.40 el kg y 1 kg de plátanos a $9.60

¿Sabes qué debes hacer para saber cuánto pagó en total por las cosas que compró?

Seguramente sabes que hay que hacer una suma, de manera que, acomodando los sumandos, alineados a partir del punto decimal, se tiene:

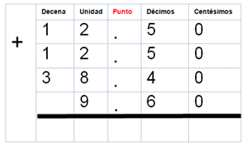
Y resolviendo la operación:

Pagaría por la compra $ 73.00 (setenta y tres pesos con cero centavos). No debes olvidar que cuando escribes la respuesta, debes indicar las unidades del problema. En este caso, se tiene un resultado monetario y hay que anotar el símbolo de pesos, indicar los centavos, y si no los hay como en este caso, debes poner dos ceros. Finalmente, nunca olvides anotar el punto decimal.

¿Cuánto pagaría si no compra los plátanos? Para responder esta pregunta tienes que modificar la operación anterior, eliminando los datos que en esta ocasión no vas a necesitar. Resolviendo la nueva operación, se tiene:

Si no lleva los plátanos debe pagar $ 63.40

Lee con atención la siguiente información que seguro te será útil al leer o escribir cantidades decimales:

Lo que hay a la izquierda del punto indica la cantidad en pesos por la compra que se realizó en el mercado. A la derecha del punto se indican los centavos considerados en la cantidad, que son 40 y que pueden escribirse como:

.40, 40₵ o 40/100

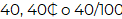
Realiza la siguiente suma:

Si quieres resolver la suma de manera horizontal, lo que debes de cuidar es tener bien ubicadas las posiciones que ocupa cada cifra que sumas para no realizar cálculos equivocados. Realiza la suma iniciando por las posiciones de la extrema derecha:

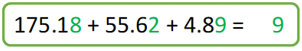
Como puedes observar, la suma de los centésimos nos da 19, por lo que, transformando 19 centésimos a décimos, se tiene 1 décimo que sumarás a la siguiente posición a la izquierda y sobran 9 centésimos que se mantienen en esa posición:

Ahora sumas los décimos. La suma da 15 y si agregas el décimo que tienes de la posición anterior, da 16 décimos. Transformando 16 décimos a la siguiente posición a la izquierda, se tienen 10 décimos que dan un entero, el cual se sumará a la siguiente posición a la izquierda y sobran 6 décimos que se mantienen en esa posición:

Ahora suma las cifras que se encuentran en la posición de las unidades. No olvides marcar el punto decimal:

Como puedes observar, la suma de las unidades da como resultado 14, más la unidad que tenías acumulada de la posición anterior, da un total de 15. Reagrupando en decenas, se tiene 1 decena que agregarás a la siguiente posición a la izquierda y 5 unidades.

Suma ahora las decenas. Se tienen 12, más la decena que tenías acumulada de la posición anterior, da un total de 13 que puedes reagrupar en 1 centena y mantener el 3 en la posición de las decenas.

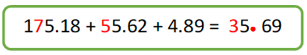
Finalmente, suma a la centena que tienes la que obtuviste del reagrupamiento anterior y obtienes la suma o resultado:

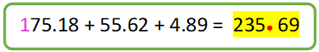
Como pues darte cuenta, sumar horizontalmente las cantidades requiere tener presente varios conocimientos como: la identificación de todas las posiciones, tener presente información específica como la de los reagrupamientos que puedes realizar y dónde los debes agregar.

Por supuesto que también puedes realizar el procedimiento de suma que ya conoces (forma vertical). Tal vez te parezca más rápido, sobre todo si tienes muchos números que sumar. En el caso de realizar la suma de esta forma sigue las siguientes recomendaciones:

• Acomoda los números de manera vertical para que los puntos decimales queden alineados.
• Resuelve la suma como si se tratara de números naturales.
• Coloca el punto decimal del resultado para que quede alineado con los puntos de los números que se están sumando.

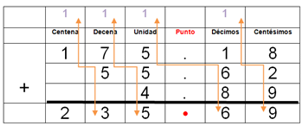
Como puedes ver, dio el mismo resultado: doscientos treinta y cinco con sesenta y nueve centésimos.

Observa con atención los siguientes números. Escribe con letras y lee cada uno.

4.05

4.50

4.5

4.500

La lectura correcta de estos números es:

4.05                Cuatro unidades cinco centésimos.

4.50                Cuatro unidades cincuenta centésimos.

4.5                  Cuatro unidades cinco décimos.

4.500             Cuatro unidades quinientos milésimos.

Como puedes darte cuenta, la lectura de estas cantidades requiere:

• Realizar la lectura de la parte entera respetando las clases de las cantidades: unidades, miles, millones etc.
• La lectura de la parte decimal se realiza como si fueran enteros, pero luego se les da el nombre de la última cifra decimal, según la posición que tenga en la serie.
• Un número decimal no se altera escribiendo o eliminando ceros a su derecha. Por ejemplo, los siguientes decimales representan la misma cantidad: .5, .50, .500

Si quieres ordenar las cantidades anteriores de menor a mayor:

4.05                4.50                4.5                  4.500

Debes hacer lo siguiente:

• Comparar primero la parte entera, en este ejemplo todas las cantidades tienen un 4 en la parte entera, por lo tanto, comparando las unidades no hay alguna que sea mayor o menor.
• Si los enteros fueran iguales (o si no existen se indica con un cero), entonces vas a comparar la parte decimal de todas las cantidades cifra por cifra.

En este ejemplo se tienen los siguientes décimos:

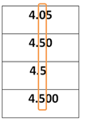
Verás que el menor décimo corresponde a 4.05 (cuatro enteros cinco centésimos), por lo que este es nuestro primer elemento en la nueva lista ordenada: 4.05

Como el resto de los décimos son todos iguales a 5 no se puede determinar cuál de las cantidades restantes en la lista es menor, por lo que se requiere comparar la siguiente posición a la derecha, es decir los centésimos, de manera que:

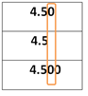
Si observas, en todas las cifras hay una ausencia de valor, es decir en todas hay o podría haber un cero:

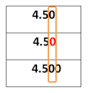
Por lo que comparando los centésimos aún no se puede determinar cuál de las cifras restantes es mayor o menor, es necesario pasar a la siguiente posición a la derecha, los milésimos:

Y aquí se repite la situación de igualdad anterior, por lo que puedes completar los espacios vacíos con ceros. De esta manera puedes concluir que las tres cifras restantes son iguales, porque 5/10 = 50/100 = 500/1000 = 1/2

Para completar el ordenamiento, puedes escribirlas cantidades restantes en cualquier orden, por ejemplo:

4.05, 4.50, 4.5 y 4.500

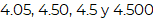
Y así completas el ordenamiento.

Analiza el siguiente ejemplo donde es más evidente el procedimiento de comparación:

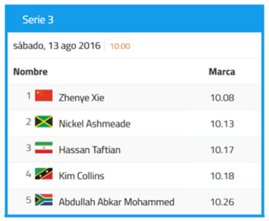
En una eliminatoria de Atletismo, 8 competidores alcanzaron los siguientes tiempos en la eliminatoria de 100 m planos.

¿Cuáles son los 5 mejores tiempos?

Para resolverlo, se tienen que ordenar los tiempos que aparecen en la tabla, a partir de los decimales, ya que todos los corredores hicieron 10 minutos y la diferencia está en la parte decimal. Recuerda que se realiza de izquierda a derecha y posición a posición, por lo que comparando los décimos se tiene:

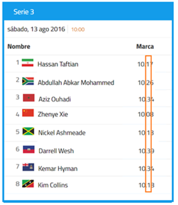
Si lo que se busca son los mejores tiempos en carrera, debes fijarte en aquellas cantidades que son menores, por lo que debes acomodarlos de menor a mayor.

Analizando y acomodando los datos, los menores décimos los tiene el corredor 4 con cero décimos, por lo que será nuestro primer tiempo en la lista:

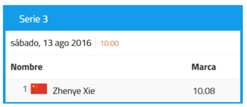
Ahora busca el segundo mejor tiempo, es decir aquéllos décimos que sean inmediatamente mayores a cero. En este caso hay tres resultados, que puedes comparar:

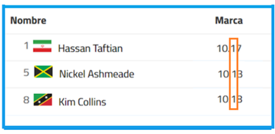
Observa que todos los décimos son iguales, por lo que aún no se puede determinar cuál tiempo es el mejor, así que se requiere comparar la siguiente posición a la derecha:

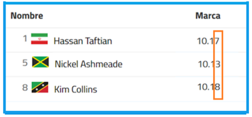
Ahora sí puedes determinar un orden. Recuerda que buscas los mejores tiempos, por lo que requieres ordenarlos de menor a mayor. Analizando los datos, el segundo mejor tiempo es el competidor 5 por que hizo 3 centésimas, le sigue el competidor 1 que logró 7 centésimas y finalmente el competidor 8 con 8 centésimas.

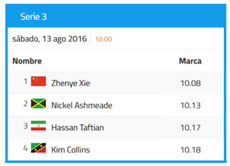
Como se buscan los 5 mejores tiempos, todavía falta un número, así que vuelve a comparar los décimos.

El quinto mejor tiempo es el décimo que le siga a 1, así que el corredor 2 logró precisamente ese tiempo, y el resto de los décimos son mayores que 2, por lo que es éste el valor que se busca.

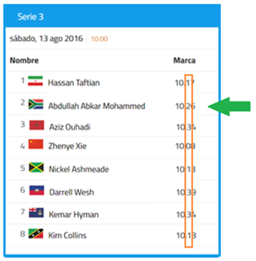
Por lo que los mejores 5 tiempos son los siguientes:

Es importante seguir las recomendaciones para resolver una suma con punto decimal, para evitar errores en el procedimiento de solución, así como lo que debes tomar en cuenta para leer, escribir y ordenar cantidades decimales.

En la siguiente sesión se abordará el caso de la resta de números decimales.

Platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.