Los polígonos de frecuencia II

Aprendizaje esperado: recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea.

Énfasis: recolectar y registrar datos en polígonos de frecuencia.

¿Qué vamos a aprender?

Estudiarás algunos conceptos matemáticos relacionados con la estadística, en particular, con los polígonos de frecuencias. Esta sesión se enfoca en aprender a recolectar y registrar datos de polígonos de frecuencia.

¿Qué hacemos?

Te has preguntado alguna vez ¿De dónde surgen las estadísticas? ¿De dónde salen los datos y cifras que escuchas, ves y lees en diferentes medios de comunicación?

Por ejemplo, sabías qué, en México, de acuerdo con el INEGI (Instituto Nacional de Estadística y Geografía) en el año 2020, más del 90 por ciento de la población entre 6 y 14 años asistía a la escuela y menos del 50 por ciento de la población entre 15 y 24 años asistía a la escuela. O que en el 2019 el 56.4 % de los hogares contaban con conexión a internet; 3.5 % más que en el año 2018.

Pero, ¿de dónde surgen estos datos?, ¿por qué son considerados como confiables?

La mayor parte de los datos se generan a partir de su recopilación y registro, a través de encuestas, conteos, sondeos, etcétera. Una vez recolectados es importante saber comunicarlos. Por tal motivo, es necesario conocer, aprender, interpretar y aplicar diferentes técnicas, conceptos y diversos procedimientos estadísticos.

Interpretar y comunicar información a través de datos es sencillo una vez que se tienen nociones estadísticas. En esta sesión aprenderás a generar e interpretar información a través de polígonos de frecuencia.

Se hizo una encuesta a 30 alumnos de segundo grado de secundaria para evaluar el servicio de una plataforma digital de música.

Específicamente se les pidió a los encuestados que asignaran una calificación del 0 al 10 de acuerdo con el grado de satisfacción; donde cero es nada satisfecho con el servicio y 10, muy satisfecho con el servicio.

Las evaluaciones que asignaron los estudiantes encuestados fueron las siguientes:

3, 0, 6, 2, 7, 9, 8, 6, 7, 7, 10, 5, 4, 8, 6, 3, 4, 5, 5, 8, 2, 6, 7, 6, 9, 4, 8, 9, 7 y 1.

¿De qué manera se pueden organizar este conjunto de datos?

¿Cuál es el grado de satisfacción más frecuente de los encuestados?

¿Es posible identificar ese dato en una gráfica?

Concentra tu atención en la siguiente gráfica.

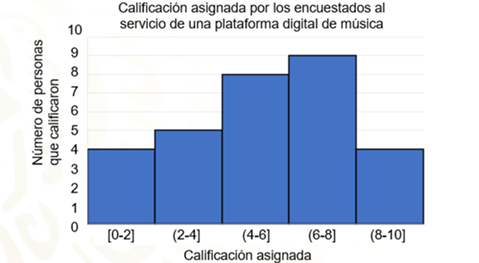
Obsérvala y, en tu cuaderno, haz una breve descripción de sus características. Para hacer tus descripciones puedes basarte en el título, los valores y nombres en cada uno de los ejes, así como otros aspectos que consideres relevantes.

La primera pregunta es: ¿De qué manera pueden organizar este conjunto de datos?

Los datos pueden ser ordenados de menor a mayor o de mayor a menor, esto permitirá identificar las frecuencias fácilmente.

Para responder la pregunta: ¿Cuál es el grado de satisfacción más frecuente de los encuestados?

Se puede recurrir a la gráfica elaborada y observar cuál es la columna que tiene mayor altura, pues mientras más alta sea una columna, es mayor el número de personas que calificaron de esa forma.

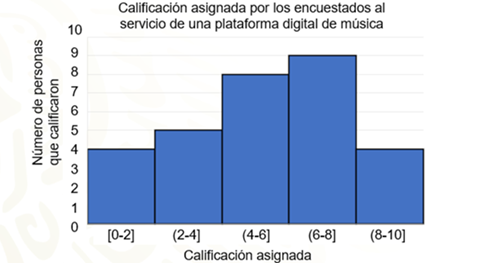
En este caso en particular, en la gráfica se puede ver la columna más alta y ésta es la que corresponde al intervalo de 6 a 8, es decir, las calificaciones más frecuentes están entre 6 y 8.

Por último ¿Es posible identificar ese dato en la gráfica? Si es posible.

Gráficas como la anterior reciben el nombre de histogramas, y su elaboración es similar a la empleada para realizar polígonos de frecuencia, incluso, es posible generar un polígono de frecuencias a partir de un histograma.

El propósito de elaborar una gráfica, cualquiera que sea, es comunicar información particularmente resumida sobre un hecho. Es importante que el título de la gráfica de una idea general de lo que se quiere representar en la gráfica, así mismo, los nombres de cada eje deben permitir comprender las interacciones entre ellos.

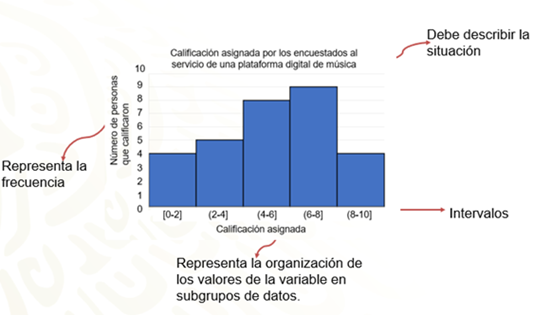
Por ejemplo, en esta gráfica, el eje vertical, o eje “y”, corresponde al número de personas que calificaron a la plataforma digital de música y los valores asignados a ese eje, corresponden a la cantidad de encuestados que asignaron cierta calificación, lo que en estadística se le puede conocer como frecuencia.

Por otro lado, el eje horizontal, o eje “x”, corresponde a las calificaciones que asignaron los participantes y los valores al intervalo de las calificaciones asignadas por ellos. Por ejemplo, el primer valor de la primera columna corresponde al intervalo de 0 a 2, es decir, en esa columna se encuentran el total de personas que asignaron calificaciones de cero, 1 y hasta 2 de calificación. El segundo intervalo corresponde a las calificaciones de 2 a 4.

En este momento, seguramente te preguntarás ¿Por qué se repite un número en cada intervalo?

Pues bien, ese número que se repite se conoce como límite, y su función precisamente es esa, fijar el inicio y fin de los datos que entran en cada intervalo.

Se dijo que el segundo intervalo es de 2 a 4, esto significa que en esa columna se encuentran el total de encuestados que asignaron una calificación mayor a 2 y hasta de 4, es decir, 3 y 4.

Si en la encuesta se hubiera solicitado asignar calificaciones con números decimales, las calificaciones 6.1, 6.5 y 6.7 ¿A cuál intervalo corresponderían? Toma un momento para analizar la situación y en tu cuaderno escribe y argumenta tu respuesta.

Esas calificaciones corresponderían al intervalo que indica de 6 a 8 de calificación, ya que el límite inferior de ese intervalo es 6 y las calificaciones al ser mayores que 6 debieran estar incluidas en ese intervalo.

Se sabe que la mitad de las personas encuestadas son mujeres y la otra mitad, son hombres. A partir de la gráfica que se presentó ¿Podrías determinar si hombres o mujeres evaluaron mejor o peor a la plataforma digital de música?, ¿cuál es el grado de satisfacción más frecuente en hombres y en mujeres? En tu cuaderno, argumenta tu respuesta.

Seguramente ya notaste que, a partir de esta gráfica no es posible dar respuesta a estas preguntas. En primer lugar, porque los datos no han sido agrupados por género y, en consecuencia, la gráfica no representa esa variable.

Comparar 2 o más variables que se refieren a la misma situación o evento a través de un histograma de frecuencias como el anterior, no es lo más apropiado, pues se corre el riesgo de que las columnas de una y otra variable obstruyan su visibilidad y, en consecuencia, no se podría comunicar la información representada de forma eficiente. Es entonces que surge la necesidad de utilizar un gráfico que cubra esas necesidades de comunicación. Uno de ellos puede ser el polígono de frecuencias, que tiene precisamente esa virtud, la de permitir comparar dos o más variables que se refieren a una misma situación.

Por ejemplo, en otra encuesta a 27 estudiantes, se registró la frecuencia de calificaciones a la misma plataforma digital de música, por género.

A continuación, se muestra la tabla de frecuencias organizada por género e intervalos. Toma un tiempo para analizarla y en tu cuaderno escribe algunas afirmaciones sobre los datos que ahí aparecen.

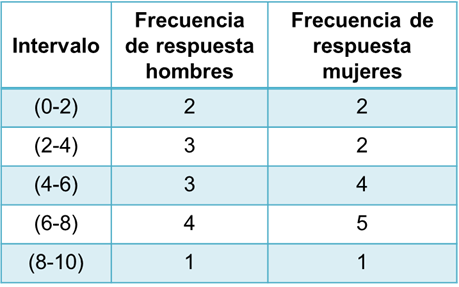
Por ejemplo, a partir de la tabla de frecuencias se puede afirmar que: Tanto mujeres como hombres evaluaron de manera similar a la plataforma digital de música, ya que las frecuencias en cada intervalo son mínimas o nulas.

Por ejemplo, el intervalo de 0 a 2, tanto en hombres como en mujeres se presenta la misma frecuencia y la diferencia es nula, por otro lado, el intervalo de 6 a 8, la frecuencia de hombres que asignaron esas calificaciones es de 4, mientras que la frecuencia de mujeres en el mismo intervalo de calificaciones es de 5, la diferencia entre ambas frecuencias es de uno. ¿Qué otras afirmaciones hiciste? Coméntalas a distancia con tus compañeras, compañeros y docente.

Ahora, pon atención a la gráfica que representa los datos de la tabla.

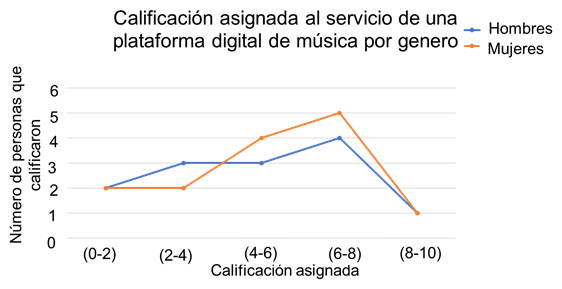
En ella se puede ver en el eje “x” los intervalos de calificación y en el eje “y”, la frecuencia de dichos intervalos.

En la gráfica se observan dos líneas. La de color naranja representa a la variable “Mujeres” y la de color azul a la variable “Hombres”. Estas líneas están formadas por segmentos de recta que se unen a través de puntos. Estos puntos representan la frecuencia de cada uno de los intervalos; a este conjunto de características se le conoce como polígono de frecuencias.

Por ejemplo, puedes observar que ambas líneas parten del mismo punto, es decir, inician en el intervalo de calificación de cero a 2, que tiene una frecuencia de 2. Esto quiere decir que el mismo número de hombres y mujeres evaluaron a la plataforma digital de música con calificaciones entre 0 y 2, es decir, no están satisfechos con el servicio que reciben.

Por otro lado, sucede algo similar con las mujeres y hombres que están muy satisfechos con el servicio que reciben, pues solamente una mujer y un hombre asignaron calificaciones entre 8 y 10, es decir, la frecuencia en ambas variables es 1.

Por último, para saber el grado de satisfacción más frecuente para mujeres y hombres, en la gráfica se puede ver que el punto más alto en la línea poligonal es el que corresponde al intervalo de 6 a 8 de calificación. 5 mujeres evaluaron a la plataforma dentro de ese intervalo, mientras que solamente 4 hombres asignaron esas calificaciones en el mismo intervalo.

Escribe en tu cuaderno algunas diferencias entre el histograma y el polígono de frecuencias. Compáralas a distancia con tus compañeras, compañeros y docente, además, elabora una conclusión al respecto.

Analiza y resuelve la siguiente situación.

Dos estudiantes realizaron una encuesta a 25 estudiantes de secundaria y 25 estudiantes de preparatoria para conocer el tiempo que dedican a la semana a usar las redes sociales más populares.

Además, también se propusieron saber a través de la mayor frecuencia, quiénes usan más tiempo a la semana las redes sociales, si los estudiantes de secundaria o los estudiantes de preparatoria.

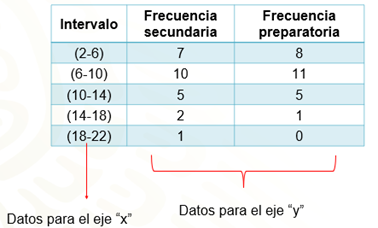
A continuación, se presenta la tabla de frecuencias que elaboraron los estudiantes con los datos recabados por su encuesta.

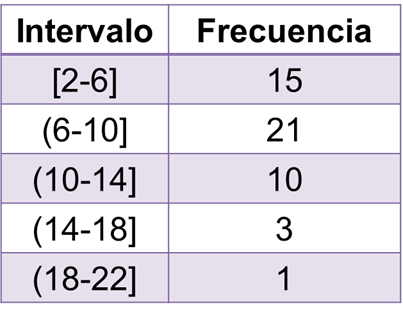
En la tabla se puede ver cada uno de los intervalos y sus frecuencias correspondientes. En el primer intervalo, de 2 a 6, se incluyen todas las respuestas de los estudiantes que dijeron usar las redes sociales 2, 3, 4, 5 o 6 horas a la semana. En el intervalo de 6 a 10, se incluyen las respuestas de los estudiantes que dijeron usar las redes sociales 7, 8, 9 y 10 horas semanales. El intervalo 10 a 14 incluye las respuestas de los estudiantes que dijeron haber usado las redes sociales 11, 12, 13 y 14 horas a la semana. En el intervalo 14 a 18, están comprendidas las respuestas de los estudiantes que dijeron usar las redes sociales 15, 16, 17 y 18 horas a la semana. Por último, el intervalo de 18 a 22, incluye la frecuencia de respuestas de los estudiantes que usan las redes sociales 19, 20, 21 y 22 horas semanales.

Nota que los límites de los intervalos tienen corchetes o paréntesis. Los corchetes indican que ese valor del límite se incluye en el intervalo y los paréntesis, que ese valor no se incluye en el intervalo. Por ejemplo, en el primer intervalo se incluyen 2 y 6 horas de uso semanal de las redes sociales, porque ambos límites tienen corchetes. Pero, en el segundo intervalo, el 6 tiene un paréntesis y el 10, un corchete, lo que indica que en este intervalo solamente se registran datos mayores que 6 y hasta los datos menores o iguales que 10.

A partir de la tabla de frecuencias, elabora la gráfica de polígono de frecuencias en tu cuaderno. Considera a los intervalos de horas en el eje horizontal “x” y las frecuencias en el eje vertical “y”.

Después, compárala con la que te presentaremos a continuación; escribe en tu cuaderno las similitudes y diferencias, reflexiona sobre ellas e identifica los aspectos en los que debes mejorar.

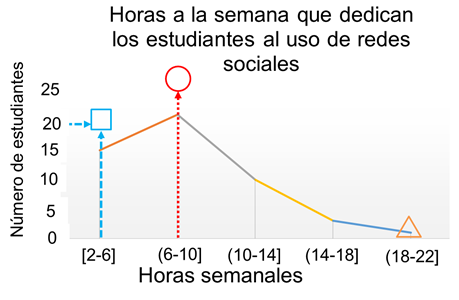
Con esta gráfica es posible responder la primera pregunta: ¿Cuántas horas dedican a la semana los estudiantes al uso de las redes sociales?

De acuerdo con la mayor frecuencia registrada, hay 21 estudiantes que dedican entre 6 y 10 horas a la semana a usar las redes sociales. Pon atención a la gráfica y verás que este intervalo de datos es justo el punto más alto de la línea poligonal, eso representa la frecuencia más alta.

¿Cuántos estudiantes dedican de 2 a 6 horas semanales al uso de redes sociales?

Son 15 estudiantes los que dieron respuestas que se consideran dentro de este intervalo de datos.

¿Existen estudiantes que no hayan dedicado tiempo al uso de las redes sociales? Observa la gráfica y argumenta tu respuesta.

Seguramente ya observaste que no hay intervalos que consideren el valor cero, por tanto, en los datos recabados, no hay estudiantes que dijeran no dedicar tiempo al uso de redes sociales.

¿Cuál es la frecuencia mínima de estudiantes y cuántas horas dedican al uso de redes sociales?

Como se puede observar, la frecuencia mínima de estudiantes es 1. Lo que indica que solamente un estudiante dedica entre 18 y 22 horas semanales al uso de redes sociales.

¿Para qué supones sean útiles estos datos? En tu cuaderno, escribe por lo menos dos ideas al respecto, después, a la distancia, discútelas con tus compañeras, compañeros y docentes.

Con la ayuda del polígono de frecuencias ya has respondido la primera pregunta. Para responder a la pregunta ¿Quiénes usan más tiempo a la semana las redes sociales, los estudiantes de secundaria o los de preparatoria? Se requiere de elaborar una nueva tabla de frecuencias y otro polígono de frecuencias que involucre las variables necesarias.

Seguramente ya notaste que falta organizar los datos por nivel educativo. A continuación, se presentan los datos que proporcionaron los estudiantes de secundaria y los de preparatoria en la encuesta.

Las respuestas de los estudiantes de secundaria son las siguientes: 3, 7, 11, 6, 10, 8, 7, 9, 4, 3, 10, 6, 4, 5, 10, 19, 14, 16, 8, 7, 11, 12, 13, 15 y 10.

Las respuestas que dieron los estudiantes de preparatoria son: 4, 2, 5, 12, 15, 8, 8, 6, 8, 9, 10, 12, 8, 9, 11, 8, 5, 5, 10, 5, 5, 13, 12, 10 y 10.

Elabora una tabla de frecuencias utilizando los siguientes intervalos:

2 a 6, 6 a 10, 10 a 14, 14 a 18 y 18 a 22. Después compara tu tabla con la que se muestra a continuación, e identifica los aspectos en que debes mejorar.

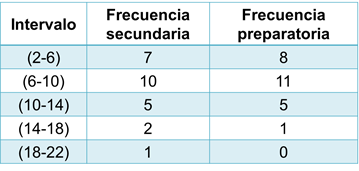
¿Esta tabla se parece a la que realizaste?, ¿cuáles son las diferencias y los puntos en común?

Con la tabla de frecuencias realizada, toma un momento para utilizarla y elaborar un polígono de frecuencias que represente los datos de la tabla.

¿Cuáles datos corresponden al eje vertical “y”? ¿cuáles datos corresponden al eje horizontal “x”? ¿qué harás para diferenciar los datos que corresponden a estudiantes de secundaria y a estudiantes de preparatoria?

Al eje “y” le corresponden los datos relacionados con las frecuencias, es decir, con el número de estudiantes que respondieron de manera particular, para ello, determina una escala que te facilite el trazado de la gráfica, por ejemplo, de 2 en 2.

Y como bien supones, al eje “x” se le asignan los datos correspondientes a cada uno de los intervalos.

Seguramente ya sabes que, para diferenciar las respuestas de los estudiantes de cada nivel educativo, tendrás que trazar una línea poligonal para las frecuencias de respuestas de los estudiantes de secundaria y otra línea poligonal para las frecuencias de respuestas de los estudiantes de preparatoria, ambas en el mismo plano cartesiano. Debes considerar el punto medio de los intervalos para localizar los puntos con los cuales trazarás el gráfico.

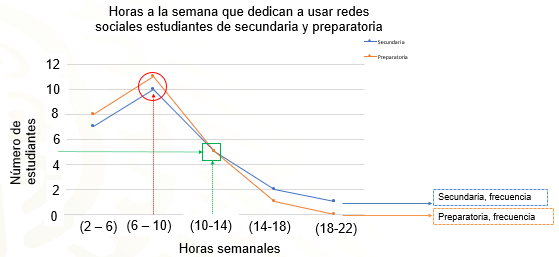
¿Qué tan parecido o diferente es al que trazaste?

¿Coinciden los datos que utilizaste en cada eje con los que se muestran en la gráfica? De no ser así, identifica los aspectos en los que puedes mejorar.

Retoma la pregunta realizada en la situación inicial, analiza el polígono de frecuencias y responde la pregunta. ¿Quiénes usan más tiempo a la semana las redes sociales, los estudiantes de secundaria o los estudiantes de preparatoria?

Si la respuesta se basa en el intervalo que mayor frecuencia tiene para cada grupo de estudiantes, se podría decir que los estudiantes de preparatoria son los que dedican más horas a la semana al uso de las redes sociales. Sin embargo, existen pruebas estadísticas que conocerás conforme avances tus estudios que te permitirán interpretar con muy alta precisión situaciones como las que te hemos presentado y analizado. Por el momento, mantendrás el análisis con base a las frecuencias que se pueden observar.

¿Qué otros datos interesantes puedes obtener del polígono de frecuencias? Toma un momento para analizar y escribe tus conjeturas en el cuaderno.

Por ejemplo ¿Qué podrías decir de las frecuencias de respuesta de los estudiantes en el intervalo que corresponde de 10 a 14 horas a la semana?

Se puede decir, que el mismo número de estudiantes tanto de preparatoria como de secundaria, dedican más de 10 horas, y hasta 14 horas a la semana al uso de redes sociales.

¿Cuántos estudiantes de secundaria y preparatoria, dedican entre 18 y 22 horas semanales al uso de redes sociales?

Toma un momento para ver la respuesta en el polígono de frecuencias.

La línea que corresponde a las respuestas de los estudiantes de secundaria, en el intervalo 18 a 22, indica que solamente un estudiante de los encuestados, dedica ese tiempo a la semana para usar las redes sociales. Por otro lado, ningún estudiante de preparatoria, de los encuestados, dedica esa cantidad de tiempo al uso de las redes sociales.

¿Tú, cuántas horas a la semana dedicas al uso de las redes sociales más populares? De acuerdo con tu respuesta ¿A qué intervalo corresponde?

En tu cuaderno escribe de qué forma podrías usar esta información para promover una cantidad responsable de tiempo para el uso de las redes sociales. Después, compara a la distancia tus argumentos con los de tus compañeras, compañeros y platíquenlos con su docente.

Recuerda que éste es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

El reto de hoy:

Copia en tu cuaderno el siguiente polígono de frecuencias e inventa para él una situación de venta de artículos que se adapte a los datos que se representan en el polígono de frecuencias. Explica a qué circunstancias corresponden los datos con mayor y menor frecuencia. Después, muestra tu trabajo a tu docente y argumenta tu elección.

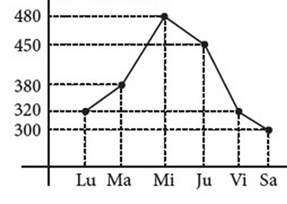
¡Buen trabajo!

Gracias por tu esfuerzo.

Descarga tu clase dando clic aquí