Los cubos en un prisma

Aprendizaje esperado: calcula el volumen de prismas mediante el conteo de unidades.

Énfasis: relaciona el concepto de volumen con la cantidad de cubos que forman un cuerpo geométrico.

¿Qué vamos a aprender?

Calcularás el volumen de prismas mediante el conteo de unidades para relacionar el concepto de volumen con la cantidad de cubos que forman un cuerpo geométrico.

¿Qué hacemos?

¿Conoces la Estela de luz que está a un lado de la avenida Paseo de la Reforma, en la Ciudad de México? Se puede identificar al pasar por ahí para ir al Zoológico de Chapultepec.

En esta sesión podrás realizar una reproducción a escala de la “Estela de luz”. ¿Conoces la historia de la “Estela de luz”?

La “Estela de luz” se construyó como parte de los festejos en el año 2010 para conmemorar el bicentenario de la Independencia de México. Es obra del arquitecto César Pérez Becerril.

Se dice que el proyecto tomó su inspiración conceptual de la tradición de los pueblos del México Antiguo.

Especialmente del pueblo maya cuyos gobernantes erigían estelas de piedra grabada para conmemorar eventos relevantes.

De tal suerte que el monumento fue concebido como dos esbeltas placas de ónix de 106 metros de altura que se iluminan en la noche. Cada estela representa cien años de independencia mexicana.

Observa bien la “Estela de Luz”, ¿Qué forma tiene?

Es un prisma rectangular, como podrás darte cuenta, muy semejante a la mayoría de las estelas mayas.

Si fueses a elaborar una maqueta similar a la “Estela de Luz”, ¿Cómo lo harías? ¿Cuántos cubos crees que deben ir en la base?

En las imágenes que observaste se puede apreciar que tiene seis cubos de largo o frente y como son dos placas, entonces podría considerarse como 2 cubos de ancho o profundo.

Falta considerar su altura. ¿Cuántos niveles de cubos tiene la estela? ¿Cuántos cubos contaste?

Al ser 106 metros de altura, es mucho, pero considera 10 niveles, para que no se caiga tu estela o maqueta.

¿Cómo cuántos cubos estimas que se necesitan en total? Quizá sean más de 100 cubos.

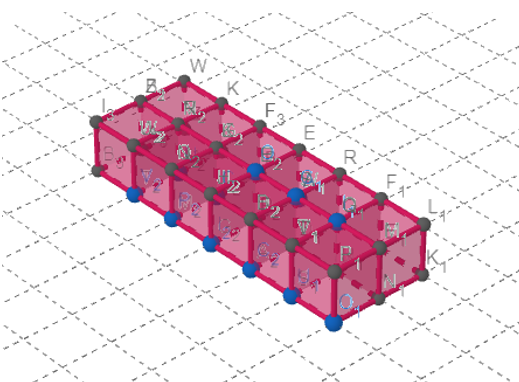
En la parte del frente, que corresponde al largo de la base, hay seis cubos y de ancho tiene dos cubos, entonces la base de la estela se compone de 12 cubos en total.

Ahora, cuántas veces se repite la base, es decir, cuántos niveles se está considerando que tenga la estela.

Que sean 10 niveles.

¿De qué manera se determina cuántos cubos en total se ocupan para construir la estela?

Si consideras que para la base se requieren 12 cubos, porque tiene 6 cubos de largo y dos de ancho. En el caso de la altura de la estela, se están considerando 10 niveles, entonces, podrías multiplicar 12 por 10, lo cual te da 120

(𝟔 ð’„𝒖𝒃𝒐𝒔×𝟐 ð’„𝒖𝒃𝒐𝒔 )×𝟏𝟎 ð’„𝒖𝒃𝒐𝒔=𝟏𝟐 ð’„𝒖𝒃𝒐𝒔×𝟏𝟎 ð’„𝒖𝒃𝒐𝒔=𝟏𝟐𝟎 ð’„𝒖𝒃𝒐𝒔𝟔 ð’„𝒖𝒃𝒐𝒔×𝟐 ð’„𝒖𝒃𝒐𝒔 ×𝟏𝟎 ð’„𝒖𝒃𝒐𝒔=𝟏𝟐 ð’„𝒖𝒃𝒐𝒔×𝟏𝟎 ð’„𝒖𝒃𝒐𝒔=𝟏𝟐𝟎 ð’„𝒖𝒃𝒐𝒔

)

Por lo tanto, son 120 cubos que se ocuparán para construir la estela.

De largo tiene 6 cubos, de ancho 2 cubos y de altura 10 cubos, por lo tanto, el número total de cubos que forman la estela o prisma son 120

Observa en tu libro de texto, página 127 Desafío 68, Cubos y más cubos. Lee la consigna.

https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/127

Consigna: En equipos construyan cinco prismas diferentes con los siguientes cubos que tienen, pueden usar todos o solo algunos, posteriormente completen la tabla.

Observa detenidamente la imagen que muestra el libro. ¿Con cuántos cubos contamos para hacer lo que solicita el desafío? Con 12 cubos.

Trabaja con doce cubos, la indicación primera dice, formar 5 prismas.

Hay que hacer 5 prismas completos con los cubos, será algo parecido a lo que trabajaste con las cajitas, solo que ahora vas a hacer completo el prisma. La unidad de medida son los cubos.

Aquí están los cubos de color naranja con la medida indicada, aristas de 4 cm, esto significa, que la medida del largo, del ancho y de la altura es de 4 cm. Siguiendo las indicaciones de lo que aprendiste la semana pasada sobre el dibujo de desarrollos planos, pudiste elaborar tu mismo o tu misma, los cubos para esta sesión.

Algo muy importante es marcar las pestañas para que cuando armes el cubo, lo puedas pegar. Observa el ejemplo del desarrollo plano con sus pestañas, para que te des una idea de cómo te debe quedar.

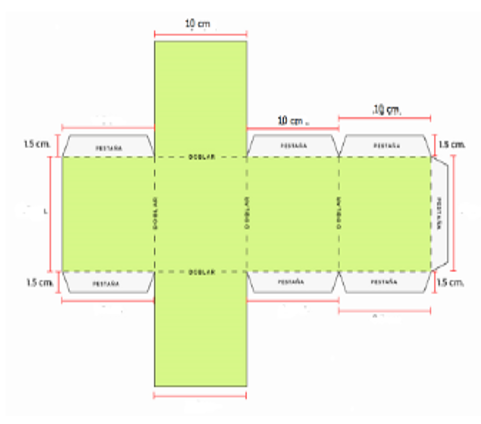
En el desarrollo plano puedes identificar las pestañas que le agregó, las cuales le sirvieron para pegar y formar sus cubos.

Para resolver el siguiente ejercicio necesitas tomar en cuenta los siguientes datos: doce cubos pequeños, que miden 1 cm de largo, 1 cm de ancho y 1 cm de altura, en estos 12 cubos, cada arista mide 2 cm.

Es momento de construir el primer prisma, considera la indicación de que puedes usar los 12 cubos o solo algunos de ellos.

Antes de armar el segundo prisma, por favor, observa que en la parte inferior de la página del libro de texto tienen una tabla en la cual debes registrar los datos de los prismas que armes.

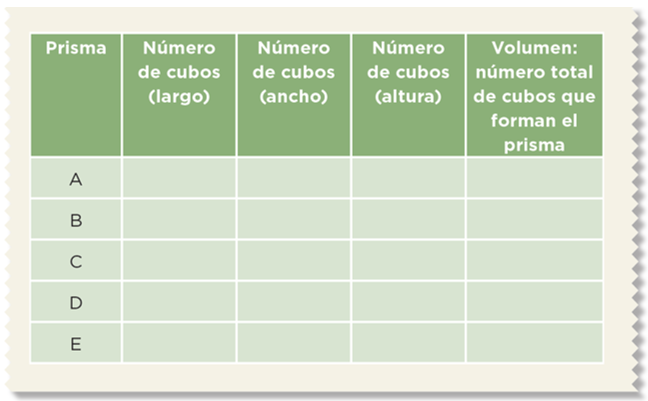
En la primera columna, vas a identificar con las letras a los prismas que armes. El primero en armar es el A. En la segunda columna, anotas la cantidad de cubos que tiene de largo; en la tercera columna, el número de cubos que tiene de ancho y, en la cuarta columna, el número de cubos que tiene de altura. Finalmente, en la última columna, la cantidad total de cubos que utilizaste para formar el cuerpo geométrico.

Observa el ejemplo:

3 cubos de largo, dos de ancho y dos de altura.

¿Cuántos cubos en total ocupa el prisma A?

Para la base se ocupan 6 cubos y como tiene dos niveles de altura, es decir, dos veces 6, son 12 cubos en total. Se registran 12 cubos en total.

El prisma B que vas a construir debe medir en alguna de sus dimensiones 3 cubos, es decir, debe tener 3 cubos de alto, de largo o de ancho.

Se ocuparon 2 cubos de largo, 2 de ancho y 3 de altura. Como de base tiene 4 cubos y son 3 niveles, entonces son 12 cubos en total.

Registra los datos del prisma B

Ahora registra los datos del prisma C: de largo, 2 cubos, de ancho, 1 y de altura son 4 En total, para armar el prisma se ocuparon 8 cubos.

Ahora arma un prisma que ocupe menos de 12 cubos y registra los datos en la tabla.

Finalmente, elabora quinto prisma, el E debe tener 10 cubos en total.

¿Cuáles son sus dimensiones? Largo, 3 cubos; ancho, 1 cubo y altura, 3 cubos, en total, tiene 9 cubos.

Ahora el prisma de los 10 cubos: largo, 5 cubos, ancho, 1 cubo y de alto, 2 cubos, en total, 10 cubos.

Observa la quinta columna de la tabla que se utilizó.

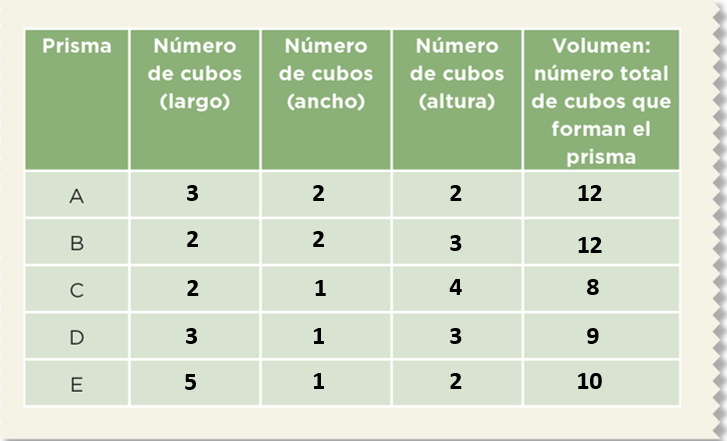
Puedes identificar que para armar el prisma A se ocuparon 12 cubos. El prisma B ocupa también 12 cubos. El C, ocupa 8 cubos en total, mientras que el prisma D está compuesto por 9 cubos y el E, en total ocupa 10 cubos. Con estos datos de cada prisma, que corresponden al número de cubos en total que ocupa cada uno, se puede también decir que ese es el volumen de cada uno de los prismas, ya que se obtiene considerando las tres dimensiones de cada uno: largo, ancho y alto.

¿Recuerdas qué es el volumen?

El volumen es el espacio que ocupa un cuerpo, en este caso sería un cuerpo geométrico.

Entonces, a partir del número de cubos que se ocupen para armar cada prisma, se puede referir a su volumen, considerando al cubo como la unidad de medida.

¿Qué es eso de ocupar al cubo como unidad de medida?

¿Recuerdas la actividad con las cajitas? Se usaron cajitas pequeñas como unidad para tratar de determinar el espacio que ocupa un cuerpo, se obtuieron valores aproximados en términos de las cajas que se ocuparon como unidad de medida, en esta ocasión, solo se han ocupado cubos como unidad de medida.

Con cubos del mismo tamaño se puede construir un prisma, aunque en los diferentes prismas se ocuparon los cubos elaborados, en otros prismas, los cubos medianos, los de 2 cm por arista, y en otros prismas, los cubos más pequeñitos, siempre se ocuparon cubos, por eso, en este caso, el cubo es la unidad de medida.

El volumen de cada prisma es de acuerdo con la unidad que se utiliza para armar cada uno, por eso la unidad en todos los casos es el cubo, ya sea en total que se formó con 12 cubos o 10 cubos, por ejemplo.

Analiza lo siguiente:

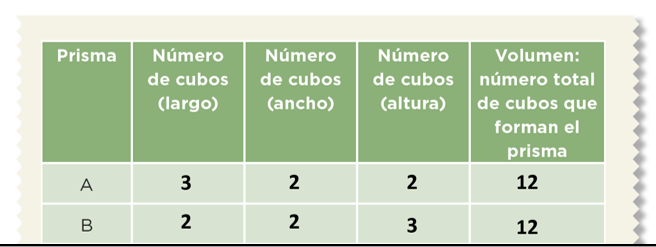
¿Qué observas entre los valores de las dimensiones del prisma A y del B?

Los dos tienen el mismo volumen, 12 cubos.

Las dos tienen el mismo volumen, entonces ¿Son prismas iguales o diferentes? es decir, ¿Tienen la misma forma?

Observa la tabla: la medida del largo es diferente, el ancho es igual y la altura es diferente, pero ocupan el mismo volumen.

Los valores de los datos son los mismos, sólo que en diferentes dimensiones, entonces ¿Son iguales o diferentes los prismas?

Observa.

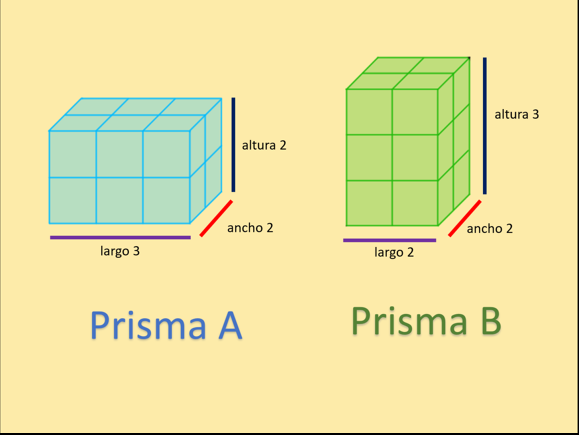
En la imagen se tiene el prisma A y el prisma B, cada uno tiene las dimensiones que se registraron en la tabla, ¿Qué sucede si cambias de posición el prisma B?

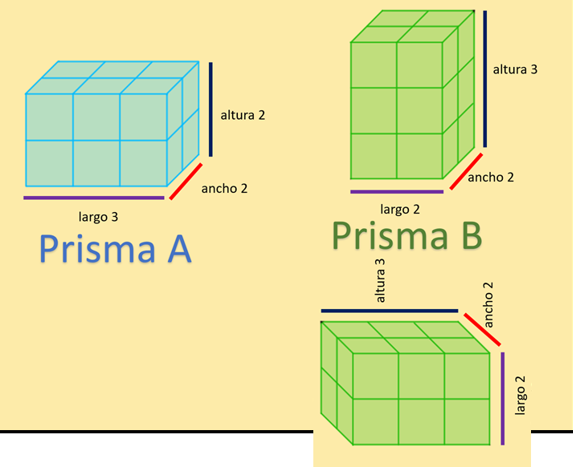
Así sí son iguales, sólo se estaba observando el prisma en una posición diferente.

De esta manera se puede apreciar que tienen el mismo volumen, porque al cambiar de posición el prisma B y reorganizar sus dimensiones, ahora hay que redefinir su largo, ancho y alto, es decir, se pueden interpretar sus dimensiones de otra manera, para comparar el valor de su volumen y comprender que es el mismo volumen, sin embargo, pueden ser prismas con formas muy diferentes.

Observen la siguiente imagen: vas a comparar las dimensiones del prisma A con las del prisma Z, ambos tienen volumen de 12 cubos. De acuerdo con las dimensiones de cada uno, ¿Es el mismo prisma?

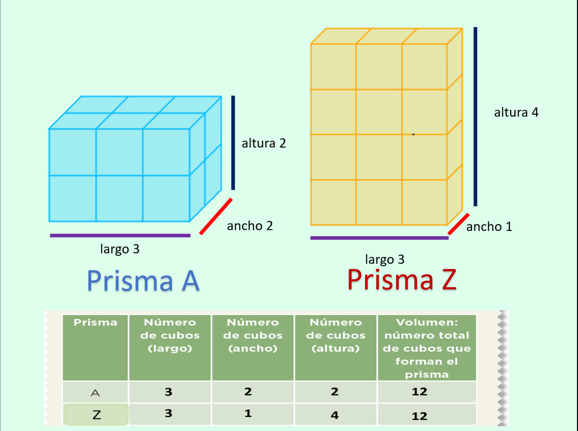
No, no son el mismo prisma, lo que observé es que las medidas de sus dimensiones no coinciden como ocurre en la comparación de los prismas anteriores.

Se deben observar las dimensiones para saber si es el mismo prisma o no. Si es posible arma los prismas para comprobarlo, sino recuerda utilizar la imaginación espacial o el desarrollo plano de los prismas.

Se tienen varias estrategias para poder comprender la forma y espacio de un prisma o de varios prismas y compararlos.

Observa el siguiente video que muestra por qué es conveniente ocupar el cubo como unidad de medida para calcular el volumen de un prisma y de los cuerpos en general.

• Video. ¿Por qué el cubo?

https://youtu.be/3f2MHue0I1c

El reto de hoy:

Comenta con algún familiar cercano uno de los ejercicios que realizaste, explícale por qué el cubo es la unidad de medida para obtener el volumen de los prismas.

Si te es posible, consulta otros libros o materiales para saber más sobre el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm

Descarga tu clase dando clic aquí