La cancha de tenis

Aprendizaje esperado: construye y usa una fórmula para calcular el perímetro de polígonos, ya sea como resultado de la suma de lados o como producto.

Énfasis: obtiene una fórmula para calcular el perímetro de un rectángulo.

¿Qué vamos a aprender?

Aprendizaje esperado: construye y usa una fórmula para calcular el perímetro de polígonos, ya sea como resultado de la suma de lados o como producto.

Énfasis: obtiene una fórmula para calcular el perímetro de un rectángulo.

¿Qué vamos a aprender?

Aprenderás a obtener una fórmula para calcular el perímetro de un rectángulo.

¿Qué hacemos?

En la sesión de hoy revisaremos cómo podemos obtener y deducir las fórmulas pertinentes para conocer el perímetro de algunos polígonos.

Para comenzar te quiero compartir un video sobre Vicente Zarazúa, ¿Sabes quién es él?

Sé que es un ex tenista mexicano y que fue medallista olímpico en 1968, por cierto, esas Olimpiadas se celebraron en México.

Observa el video.

• Los juegos de la amistad.

https://www.youtube.com/watch?v=4EtmD_s0f4U )

Que buen deportista, es indudable que ese tipo de logros inspiran y dan un orgullo peculiar de ser mexicano, esperemos que tengamos más participantes en este deporte.

¿Qué figura geométrica tendría la cancha de tenis?

R = Se juega en una cancha con forma de Rectángulo.

¿Qué figura geométrica tienen las zonas en que se divide?

R = Las zonas de juego son también rectángulos.

Vamos a entrenar matemáticas a través del “Deporte Blanco”, como le dicen al tenis, sigamos con preguntas. Tomando en cuanta toda la cancha y sus zonas. ¿Cuántos rectángulos se forman?

R = Son once rectángulos, uno de la cancha y diez de las zonas.

Si tuviéramos que calcular el perímetro de cada rectángulo de la cancha de tenis con las siguientes medidas, cómo lo resolverías.

Recuerda que el perímetro es la cantidad de unidades lineales que caben en el contorno de la figura.

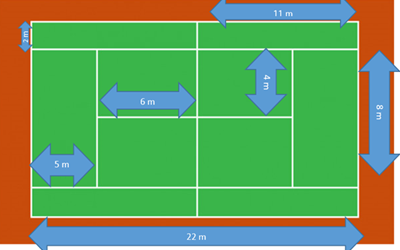
Estas son las medidas que tenemos de nuestra cancha de tenis, cómo lo resolverías.

R = Primero voy a calcular el perímetro del rectángulo que tiene las siguientes medidas 11 metros de ancho y 2 metros de largo, cómo el perímetro es el contorno. Este rectángulo tiene como perímetro 26 metros.

¿Qué operaciones realizaste para calcular el perímetro que te fue tan sencillo encontrar?

R = Sumé la longitud de todos los lados, 11 + 2 + 11 + 2 y eso nos da 26 metros de perímetro.

Vamos a escribir una fórmula: usemos “P” para identificar el perímetro, “a” para la altura de este rectángulo y “b” para su base, entonces nos quedaría así, P = a + b + a + b.

Los rectángulos tienen 2 alturas y 2 bases, entonces esta fórmula la puedes usar para calcular el perímetro de todos los demás rectángulos, todos tienen 4 lados, y 2 que son paralelos corresponden a la altura y 2 que también son paralelos entre ellos corresponden a las bases.

Si multiplicas la altura por dos, porque son dos alturas las que tiene cada rectángulo y multiplicas la base por 2, porque también son dos bases las del rectángulo y sumas esas dos multiplicaciones, te da el total del perímetro.

Entonces nuestra fórmula quedaría así P = (2 x a) + (2 x b), pero verifiquemos si en verdad obtenemos el mismo resultado, te pido que realices las operaciones para que verifiques conmigo.

Veamos, si lo que escribimos nos lleva al mismo resultado: primero debemos hacer las operaciones que están dentro del paréntesis: 2 por 11 son 22, 2 por 2 son 4, y lo sumamos son 26 metros, es el mismo resultado que obtuvimos sumando todos los lados.

Tenemos dos formas diferentes para calcular el perímetro de un rectángulo, la primera es sumando la medida de todos sus lados, y la segunda es multiplicar por dos su atura y también multiplicar por dos su base, al final los dos productos se suman.

Recuerda que puedes usar cualquier procedimiento, ambos te llevan al resultado correcto.

Es correcto decir base y altura es común cuando estamos hablando de una imagen del rectángulo dibujada, por ejemplo, en el cuaderno, pero cuando se habla de terrenos o de objetos que tienen forma rectangular es común indicar largo y ancho.

Entonces podemos decir que la cancha tiene largo y ancho y los rectángulos que le dibujan dentro también.

Ahora, te voy a presentar nuevamente la imagen con las medidas que tiene esta cancha de tenis y calculemos el perímetro del rectángulo que forma toda la cancha.

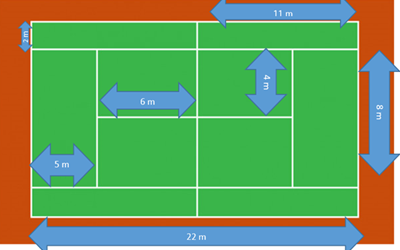
¿Cuánto mide una cancha de tenis?

R = De largo, la cancha mide 22 m y de ancho mide, son 8 metros del rectángulo de en medio, más dos metros de cada rectángulo que está a los lados, son 12 metros de un lado y 12 metros del otro lado son 24 más 22 + 22 son 68 metros de perímetro.

Ahora vamos a calcular el perímetro del rectángulo que mide 6 metros de largo y 4 de ancho, para practicar esto que acabamos de estudiar.

Son 6 m por 2 son 12 metros y 4 metros por 2 son 8 m, ahora sumo 12 más 8, el perímetro de este rectángulo es de 20 metros.

Espero que tengas el mismo resultado del perímetro del rectángulo que mide 6 m de largo por 4 m de ancho son 20 metros, si no fue así, revisa dónde hubo diferencias.

Ahora calculemos el perímetro del rectángulo de 8 metros de largo y 5 metros de ancho.

Veamos, de largo son 8 metros más 5 metros de ancho son trece, por 2 son 26 metros de perímetro tiene este rectángulo.

¿Cómo calculaste ese perímetro? ¿Llegaste al mismo resultado que nosotros?

El perímetro lo podemos emplear en muchas situaciones, por ejemplo, para medir la orilla de un terreno que se quiere bardear o hacer el recuadro para una fotografía o trazar una cancha de juego.

Vamos a resolver el desafío número 69 ¿Cuánto mide? que se encuentra en página 130 de tu libro de Desafíos Matemáticos.

Leamos la situación.

La familia Pérez compró una casa y desea hacerle arreglos; entre otros, cambiar las puertas y ventanas. Para hacer ventanas de aluminio, el herrero cobra por metro lineal, por lo que es necesario saber cuántos metros lineales de aluminio se necesitan. Si cada ventana mide 85 centímetros de base y 120 centímetros de alto.

Las personas que colocan ventanas también deberán calcular el perímetro, para saber cuánto material van a emplear.

¿Te das cuenta que los conocimientos matemáticos se pueden aplicar en, prácticamente, cualquier actividad?

Vamos a responder la primera pregunta, ¿qué cantidad de aluminio se necesitará para construir una ventana con esas medidas?

Como ya sabemos, para calcular el perímetro de un rectángulo podemos sumar las bases y las alturas, entonces sumo 85 cm, más 120 cm, son 205 cm, más 85 cm son 290 cm, más 120 cm, son 410 cm tiene de perímetro esta ventana.

Ahora vamos a ver si sale el mismo resultado con otro procedimiento, voy a multiplicar 85 cm x 2 y 120 cm por 2, y me da 170 más 240, tengo los 410 centímetros de perímetro.

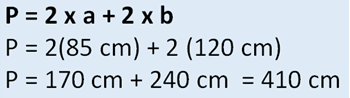
Entonces se necesitan 410 centímetros de material para una ventana, pero fíjate que la familia Pérez va a hacer 4 ventanas, ¿Cuánto material se necesita?

Yo sumaría cuatro veces 410 para obtener el total. Haciendo las sumas, el material que se necesita son 1640 centímetros.

También podemos realizar una multiplicación, la cantidad de material de una ventana por cuatro, esto es, multiplicar 410 cm por 4 y nos da como resultado 1640 centímetros, llegamos al mismo resultado.

Para convertir 1640 centímetros a metros, como vamos de una unidad menor a una mayor, dividimos en este caso es entre 100 pueden utilizar su calculadora para obtener el resultado 1640 centímetros es igual a 16.40 m, esta es la cantidad que se requiere en metros para las 4 ventanas.

Sigamos con la pregunta b, ¿qué forma geométrica tienen las ventanas?

R = Tienen forma de rectángulo, igual que la cancha de tenis y todas las zonas que la forman.

¿Y cómo podemos encontrar el perímetro de esa figura?

R = Una forma consiste en sumar la medida de todos sus lados.

Sumando la longitud de sus lados, pero ¿Recuerda que también encontramos otra manera de calcular el perímetro de los rectángulos?

Como el rectángulo tiene dos lados largos o bases iguales y dos alturas también iguales, podemos multiplicar la medida de su base por 2 y la de su altura también por dos, luego sumamos el resultado de las dos multiplicaciones.

Observaste que con las dos formas de calcular el perímetro llegamos al mismo resultado.

Entonces nos pide que escribamos una fórmula. Podemos escribir la primera fórmula como: P es igual a altura más base más altura más base, otra fórmula que es equivalente a esta sería: P es igual a 2 x a + 2 x b

Ya comprobamos que empleando cualquiera de estas dos fórmulas llegamos al mismo resultado.

Vamos a recapitular lo que aprendimos: Que el perímetro es la medida del contorno de una figura y obtuvimos dos fórmulas para calcular el perímetro de cualquier rectángulo, una consiste en sumar la medida de cada uno de sus lados y la otra en multiplicar la altura por dos y la base también por dos, para después sumar ambos resultados.

Recuerda que puedes utilizar el procedimiento que más se te facilite para llegar al resultado, sigue practicado, por ejemplo, encontramos que el tenis, también conocido como “El deporte Blanco” fue un buen punto de partida para aplicar los contenidos que estamos estudiando. Puedes encontrar nuevas posibilidades de la aplicación de las matemáticas al entorno que nos rodea.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P5DMA.htm

Descarga tu clase dando clic aquí