Construyendo figuras
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Aprendizaje esperado: construye y usa el m2, el dm2 y el cm2
Énfasis: utiliza diferentes unidades de medida de superficie (m2, dm2 y cm2) para dibujar figuras con áreas determinadas.
¿Qué vamos a aprender?
Aprenderás lo que son las figuras con diferentes superficies, construyendo figuras de diferentes tamaños utilizando cuadrículas y utilizando distintas unidades de medida.
¿Qué hacemos?
Observarás las diferentes unidades de medida que se revisaron en la sesión anterior. Sólo que ahora verás cómo todo eso que aprendiste, se aplica en algunas representaciones gráficas.
Para comenzar con la sesión realizarás una serie de juegos en el que se te ira indicando la medida del área de una figura, por ejemplo 10 centímetros cuadrados y tú vas a trazar una figura en tu cuaderno que tenga esa área, cada cuadrito es un centímetro cuadrado.
Observa la siguiente imagen.
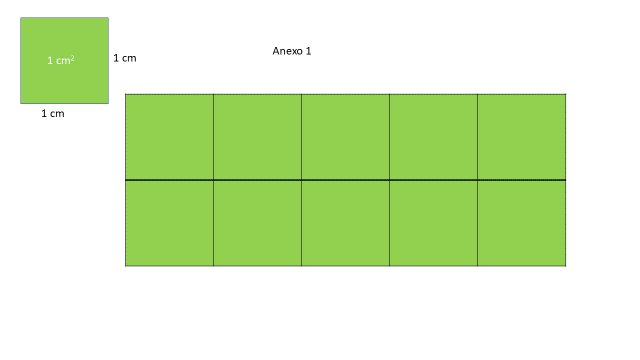
Fíjate bien, aquí puedes ver que la figura tiene 10 cuadritos de un centímetro por lado, por lo que su área mide 10 centímetros cuadrados.
Es un rectángulo y sus lados miden 2 centímetros de alto por 5 centímetros de ancho, así que su área mide 10 centímetros cuadrados.
¿Y cuántos decímetros cuadrados representa esa figura?

Un centímetro cuadrado, ¿Qué parte del decímetro cuadrado representa?
Un centímetro cuadrado cabe 100 veces en un decímetro cuadrado, dicho de otra forma, un decímetro cuadrado tiene 100 centímetros cuadrados.
Entonces, ¿Cuántas veces cabe la figura que mide 10 centímetros cuadrados en un decímetro cuadrado?
Observa la relación que tienen los centímetros cuadrados con los decímetros cuadrados. Cuántas veces cabe el rectángulo que mide 10 centímetros cuadrados en un decímetro cuadrado.
Cabe 10 veces, es decir que 10 centímetros cuadrados son la décima parte del decímetro cuadrado.

La equivalencia entre decímetros cuadrados y centímetros cuadrados es diferente a la que hay cuando no son cuadrados.
En los decímetros y centímetros lineales, la equivalencia es de 10 es decir, en un decímetro lineal caben 10 centímetros lineales, pero en las unidades cuadradas, la equivalencia es de 100 como viste antes.
Para hacer conversiones entre unidades cuadradas hay que considerar que van de 100 en 100
Ahora observa la equivalencia entre el decímetro cuadrado y el metro cuadrado.

Un metro lineal tiene 10 decímetros, pero un metro cuadrado tiene 100 decímetros.
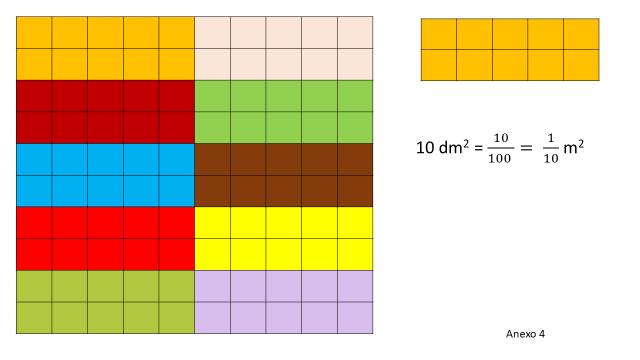
Entonces si tienes 10 decímetros cuadrados puedes ver que caben 10 veces en un metro cuadrado. La equivalencia entre dos unidades cuadradas consecutivas es 100
Si una figura tiene 5 decímetros cuadrados de área, ¿Cómo podrías dar la medida en centímetros cuadrados?
Si un decímetro cuadrado tiene 100 centímetros cuadrados, entonces, tendrías que multiplicar 5 por 100 y la respuesta sería 500 centímetros cuadrados
Para convertir de metros cuadrados a decímetros cuadrados se multiplica por 100 y de decímetros cuadrados a centímetros cuadrados también se multiplica por 100
¿Y las demás unidades de medida cuadradas también tienen la misma relación?
Entre cada unidad cuadrada y la que le sigue es la misma relación. Si quieres calcular un área en la misma unidad de medida no hay problema porque es directo, pero si quieres encontrar a cuánto equivale en otra unidad, ya sea mayor o menor, deberás fijarte en la equivalencia, de acuerdo con la relación que haya entre ellas.
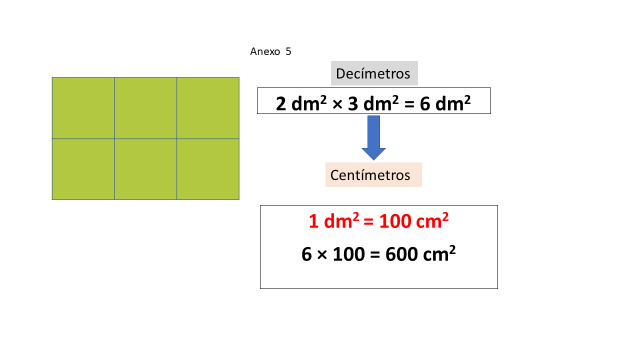
Observa, tienes un rectángulo que mide dos decímetros de altura por 3 decímetros de largo, como las unidades de sus lados son las mismas, entonces el área se obtiene directamente multiplicando ambas. Pero si quieres obtener esa medida en centímetros cuadrados, debes recordar que un decímetro cuadrado tiene 100 centímetros cuadrados, por lo que el área del rectángulo tendrá que multiplicarse por 100 para obtener la medida en los centímetros cuadrados que quieres.
Recuerda que en las unidades cuadradas debes multiplicar por 100 si quieres pasar de una unidad a la que le sigue.
Podrías hacer una tabla con estas equivalencias, para que no se te olviden.
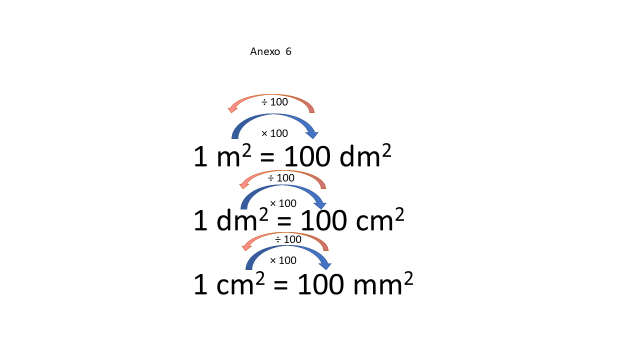
Si quieres pasar de una unidad mayor a una menor inmediata multiplica por 100 si quieres pasar de una menor a una superior inmediata, entonces divide entre 100
Esto te ayuda a recordar la relación entre unidades cuadradas.
El reto de hoy:
Te invito a que abras tu libro de desafíos en la página 166 donde se encuentra el desafío 88 con el título, ¿Cómo es?

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/166
El desafío dice así: En equipos hagan lo que se pide a continuación. Utilicen los cuadrados del desafío anterior y construyan una figura que corresponda a cada una de estas medidas.
Construye las figuras con las medidas de los incisos. Recuerda cuál es la relación que hay entre las unidades de medida cuadradas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P4DMA.htm



Login to join the discussion